Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
Since elementary school, you've been doing division. The following theorem is a crucial beginning place for much of our work in abstract algebra. It gives a formal meaning to the quotient and remainder when performing division.
Theorem (Division Algorithm)
Let $a,n\in\mathbb{Z}$, with $n> 0$. Then there exists unique integers $q$ and $r$ (called the quotient and remainder) such that $a=qn+r$ where $0\leq r<n$.
Anytime you see a new word, a new theorem, a new problem, etc., making an example to illustrate the new idea is crucial, as well as being able to recognize when something closely related is not an example. As the semester progresses, we'll be doing this with each new problem we work on. Sometimes the problem itself will ask you to create the example, and sometimes you'll just need to make it yourself. Here's an example of how to give an example and non example of the theorem given above.
Example
If we let $a=23$ and $n=5$, then we can write $23=4\cdot 5+3$. The quotient is $q=4$ and the remainder is $r=3$. Notice that $0\leq r<5$.
Non Example
Let $a=-23$ and $n=5$. We can write $-23=(-4)\cdot 5-3$, so it might be tempting to say that the quotient is $q=-4$ and the remainder is $r=-3$. However notice that it is not true that $0\leq r<5$. The remainder cannot be negative, and must be less than $n$. Instead we can write $-23=(-5)\cdot 5+2$. This means the quotient is $q=-5$ and the remainder is $r=2$.
We'll come back to the division algorithm very soon, and give a formal proof. You are welcome to start working on the proof now for homework. You'll see the division algorithm show up in several places as you work the first few weeks of problems.
Problem 1 (The Game Of Scoring)
The game of Scoring is a two-player game. Start by creating a pile of $n\geq 1$ objects (feel free to choose $n$ however you want). On each player's turn, they must choose 1, 2, or 3 items from the pile. Players alternate taking turns until someone takes the last object. Whoever takes the last object wins.
- Play this game several times with various values of $n$.
- For which values of $n$ does the first player have a winning strategy (meaning they are guaranteed to win if they play correctly). Remember to always fully justify your answers.
- For which values of $n$ does the second player have a winning strategy? Why?
- For which values of $n$ does the first player have a winning strategy if we change the rules so that now each player must choose 1, 2, 3, or 4 items from the pile.
- We'll now change the rules and require a player to take anywhere from 1 to $k$ objects each turn. Conjecture the values of $n$ for which the first player has a winning strategy.
Problem 2 (The Game Of Scoring Misere)
A misere game is a game played by the regular rules with one change; whoever wins the game according the regular rules is the loser. Consider again the game of Scoring, but this time we'll play it as a misere game.
- For which values of $n$ does the first player have a winning strategy when playing misere, provided each player must take 1, 2, or 3 objects?
- For which values of $n$ does the first player have a winning strategy when playing misere, provided each player must take 1, 2, 3, or 4 objects?
- If instead a player must take between 1 and $k$ objects, conjecture the values of $n$ for which the first player has a winning strategy when playing misere.
Definition (Encryption Key)
An encryption key is an algorithm which specifies how a message is to be encoded. The encrypted message is often called ciphertext. The original message is called plain text. See Wikipedia for more information.
Definition (Simple Shift Permutation Of The Alphabet)
Let $M$ be a message, which we will think of as a sequence of letters from the standard 26 letter Roman alphabet. We can write $M=(m_1,m_2,m_3, \ldots, m_n)$ where $m_i\in\{a, b, c, \ldots, z\}$. For simplicity, our messages are not case-sensitive and all spaces and punctuation have been removed. To send the phrase "Let's meet at dawn." we'd just use the plain text message $M=(l,e,t,s,m,e,e,t,a,t,d,a,w,n)$.
We now define an encryption key to produce ciphertext from a message $M$. Given a message $M=(m_1,m_2,m_3, \ldots, m_n)$, let $\phi_3(m_i)$ be the letter in the alphabet that has been shifted three right from the current letter. When we hit the end of the alphabet, we'll wrap around so that shifting $z$ right one gets us to $a$. Let's call this the simple shift permutation $\phi_3$. So we now have $\phi_3(a)=d$, $\phi_3(m)=p$, and $\phi_3(z)=c$. In a similar manner, we can define the simple shift permutation $\phi_n$ which shifts each letter right $n$ units.
Problem 3 (First Encryption Key)
Suppose you encounter some ciphertext $(i,q,x,x,p,a,z,q)$ that you know has been encrypted using a simple shift permutation $\phi_n$ for some $n$.
- Decode the ciphertext and state the original message. State the value of $n$ that was used to encode the original message.
- Encode the plain text message "attack at dawn" into ciphertext using the same encryption key you discovered in the first part.
- Are there any other $n$ that would have produced the same results as above? Be ready to fully justify your answer.
Problem 4 (The Set Of Simple Shift Permutations)
Let $S = \{a,b,c,\ldots,z\}$ be the set of letters in the Roman alphabet. For each $n\in\mathbb{Z}$, let $\phi_{n}:S\to S$ represent the encryption key that shifts each letter in the alphabet right $n$, where we wrap around from $z$ to $a$ for letters that need to be shifted past $z$. So $\phi_3(a)=d$, $\phi_3(b)=e$, and $\phi_3(z)=c$. We've called this a simple shift permutation of $S$.
- For which $n$ does $\phi_n$ not change the message?
- Consider the encryption key $\phi_{9}$, which shifts each letter right 9. If a message had been encrypted using $\phi_9$, then clearly $\phi_{-9}$ would decrypt the message as $\phi_{-9}(\phi_9(s))=s$ for any letter $s$. Give a positive integer $n$ that we could also use to decode a message that has been encrypted using $\phi_9$.
- Does $\phi_{30}=\phi_7$? Does $\phi_{33}=\phi_7$? For which $n$ does $\phi_n=\phi_7$? Explain.
- Consider the set of all shifts of $S$, namely $H=\{\phi_n\mid n\in\mathbb{Z}\}$. How many different functions are in $H$? Prove your answer is correct.
Definition (Permutation)
Let $X$ be a set. A $\textdef{permutation}$ of $X$ is a bijection from $X$ to $X$, so it's a function from $X$ into $X$ that is both one-to-one and onto. We can think of a permutation of $X$ as a way of rearranging the elements in $X$. The identity permutation is the permutation $id_X:X\to X$ defined by $id_X(x)=x$.
Problem 5 (Number Of Permutations)
Given finite set $X$ with $n$ elements, how many permutations are there of $X$?
- Show that if $X=\{1\}$, then there is only one permutation of $X$.
- Show that if $X=\{1,2\}$, then there are two permutations of $X$. List them.
- Make a list of all permutations of $X=\{1,2,3\}$, and then of $X=\{1,2,3,4\}$. What pattern do you see?
- Make a conjecture about the number of permutation of $X$ if $|X|=n$. Then prove your conjecture.
Definition (Automorphism Of A Graph)
An $\textdef{automorphism of a graph}$ is a permutation $\sigma$ of the set of vertices such that two vertices $x$ and $y$ form an edge if and only if $\sigma(x)$ and $\sigma(y)$ form an edge. The $\textdef{automorphism group of a graph}$ is the set of all automorphisms of the graph. If $\mathcal{G}$ is a graph, its automorphism group is denoted $\aut(\mathcal{G})$.
Problem 6 (Automorphisms Of A Square)
Consider the graph $\mathcal{G} = (V,E)$ drawn below. The vertex set is $V = \{1,2,3,4\}$ and the set of edges is $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$
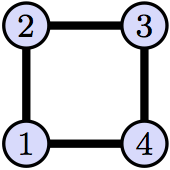
Write down all the automorphisms of $\mathcal{G}$ (there are more than 4, but less than 10). Explain how you know you have listed every automorhpism of $\mathcal{G}$.
This problem continues in AutomorphismsOfASquare2.
Problem 7 (Automorphisms Of A Square 2)
Again consider the graph $\mathcal{G} = (V,E)$ shown below with vertex set $V = \{1,2,3,4\}$ and edges $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$

Recall that set of all automorphisms of $\mathcal{G}$ is written $\aut(\mathcal{G})$. We listed all the elements in this set in problem AutomorphismsOfASquare. Determine if each statement below is true or false. Make sure you justify your answers.
- There is an automorphism $a\in \aut(\mathcal{G})$ such that $a^2=a\circ a$ (the composition) is the identity automorphism, but $a$ is not the identity.
- There is an $a\in \aut(\mathcal{G})$ such that $a^3=a\circ a\circ a$ is the identity but $a$ is not the identity.
- There is an $a\in \aut(\mathcal{G})$ such that every other $b\in \aut(\mathcal{G})$ is of the form $b=a^n$ for some $n$. [Hint: for each element in $\aut(G)$, find the smallest $n$ such that $a^n=id_V$. ]
- For every $a,b\in \aut(\mathcal{G})$, we have $a\circ b = b\circ a$.
Problem 8 (Automorphisms Of A Directed Square)
Consider the directed graph $\mathcal{G} = (V,A)$ shown below with vertex set $V = \{1,2,3,4\}$ and arrows (directed edges) $$A = \{(1,2),(2,3),(3,4),(4,1)\}.$$

- How would you define an automorphism of a directed graph?
- List all the automorphisms of this directed graph. You should have 4.
- Is there is an automorphism $a\in \aut(\mathcal{G})$ such that $a^2=a\circ a$ (the composition) is the identity automorphism, but $a$ is not the identity?
- Is there is an $a\in \aut(\mathcal{G})$ such that $a^3=a\circ a\circ a$ is the identity but $a$ is not the identity?
- Is there is an $a\in \aut(\mathcal{G})$ such that every other $b\in \aut(\mathcal{G})$ is of the form $b=a^n$ for some $n$?
- For every $a,b\in \aut(\mathcal{G})$, do we have $a\circ b = b\circ a$?
Problem 9(Simple Shift Repetition)
Let's now devise a way to not only encrypt a message, but also keep track of who has seen the message? There are several ways to do this. Let's look at an example that involves repeated application of the same encrpytion key. For this example, let's use the encryption key $\phi_4:S\to S$ (the simple shift permutation that shifts right 4).
A group of military commanders decide to send messages using a message chain. The message passes sequentially from one person to the next, where at each stage they apply the encryption key to the ciphertext before sending it on. If I want to send the plain text message $attackatdawn$, then I'd send the message $exxegoexhear$ to the person after me in the chain. This person would decipher the text using $\phi_4^{-1}$ (shift left 4), and then apply $\phi_4$ to the cipher text $exxegoexhear$ and then send the ciphertext $ibbiksibliev$ to the person after them in the chain. This would repeat until the message made it to every commander.
- You receive the cipher text $skkzgzkomnz$. What is the plain text message? How many people have seen this message?
- How many commanders can we include in this encryption scheme and still tell who sent the message?
- If we use $\phi_5$ instead of $\phi_4$, how many commanders can we include in this encryption scheme and still tell who sent the message?
- Is there an encryption key $\phi_n$ so that $\phi_n^2=\phi_0$. In other words, is there an encryption key $\phi_n$ that will only allow up to two commands to be in the chain?
Problem 10 (Cryptography Reading Assignment)
Download the free open source book Abstract Algebra: Theory and Applications by Thomas W. Judson. See http://abstract.ups.edu/. (For a direct link use http://abstract.ups.edu/download/aata-20160809.pdf .)
- Read pages 76-81. This is chapter 7, Introduction to Cryptography. It's OK if you don't understand all the notation.
- Come with at least three questions about parts of the reading you would like to understand more about.
It's OK if you don't understand all of the reading. He uses some theorems and notation that we have not yet covered. If you want to know more about how some of the things worked in the reading, please make sure you ask a question.
Once we have a set of permutations, we'd like to be able to combine them to get new permutations. The previous problem used repetition on simple shift permutations of the alphabet to obtain additional permutations. The next problem has you show that the composition of any finite collection of permutations on a set is always a permutation.
Theorem (The Composition Of Permutations Is A Permutation)
Let $X$ be a set. Suppose that $\sigma_1, \sigma_2, \ldots,\sigma_k$ are permutations of $X$. Then the composition $\sigma_1\circ \sigma_2\circ \ldots\circ \sigma_k$ is a permutation of $X$.
Problem 11 (The Composition Of Permutations Is A Permutation)
Prove theorem (The Composition Of Permutations Is A Permutation). As some reminders, you may use the following facts that you proved in either Math 301 or Math 340. You may use these facts without proof.
- The composition of two injective functions is injective.
- The composition of two surjective functions is surjective.
- A function is a bijection if it is both injective (1 to 1) and surjective (onto). Hence, the composition of two bijective functions is a bijection.
- You might find induction helps you get from a composition of two bijective functions is bijective to the composition of $n$ bijective functions is bijective.
Remember, anytime you see a new theorem, definition, idea, etc., start by making an example, and a non example. If someone in class wants to see an example, I'd love to have you share your work there.
Problem 12 (Do We Need The Associative Law)
In this problem, your job is to explain each step in the process of solving $2x=3$ for $x$. Try to break each part of your computation down into the most basic processes. The only two operations we have on the real numbers are addition and multiplication. Subtraction and division are inverse operations, so rather than saying "divide by 2", you would multiply by the multiplicative inverse of 2. As always, write your solution using complete sentences.
- If you did not use the associative law of multiplication in your work, then go back through your work. It should be there somewhere.
- Did you use the commutative law of multiplication in your work? If you did, make sure you pinpoint where you did. It is possible to solve this problem without the commutative law.
- You might try to justify this as follows:
First divide both sides of $2x=3$ by 2. Then cancel the 2's on the left side of the equation and we have $x=3/2$.
Exercise (Simple Matrix Encryption)
Consider the matrix $A = \begin{bmatrix} 2&1&-1\\ 5&2&-3\\ 0&2&1\end{bmatrix}$. Joe decides to send a message to Sam by encrypting the message with the matrix $A$. He first takes his message and converts it to numbers by replacing A with 1, B with 2, C with 3, and so on till replacing Z with 26. He uses a 0 for spaces. After replacing the letters with numbers, he breaks the message up into chunks of 3 letters. He then multiplies each chunk of 3 by the matrix $A$, resulting in a coded message. For example, to send the message "good job ben" he firsts converts the letters to the numbers and places them in a large matrix $M$ (top to bottom, left to right) $$ \left[ \begin{bmatrix}g\\o\\o\end{bmatrix}, \begin{bmatrix}d\\ \ \\ j\end{bmatrix},\begin{bmatrix}o\\b\\\ \end{bmatrix},\begin{bmatrix}b\\e\\n\end{bmatrix}\right] \rightarrow \left[\begin{bmatrix}7\\15\\15\end{bmatrix}, \begin{bmatrix}4\\0\\10\end{bmatrix},\begin{bmatrix}15\\2\\0\end{bmatrix},\begin{bmatrix}2\\5\\14\end{bmatrix}\right] = M= \begin{bmatrix} 7 & 4 & 15 & 2 \\ 15 & 0 & 2 & 5 \\ 15 & 10 & 0 & 14 \end{bmatrix} .$$ To encode the matrix, he computes $$AM = \begin{bmatrix} 14 & -2 & 32 & -5 \\ 20 & -10 & 79 & -22 \\ 45 & 10 & 4 & 24 \end{bmatrix}.$$ and then sends the numbers \([ [ 14, 20, 45], [ -2, -10, 10], [ 32, 79, 4], [ -5, -22, 24] ]\) to Sam. Sam uses the inverse of $A$ to decode the message.
- Use $A^{-1}$ to decode \([ [ 14, 20, 45],[ -2, -10, 10],[ 32, 79, 4],[ -5, -22, 24] ]\) and show the message is "good job ben."
- Decode the message \([[39, 89, 22],[20, 48, 4],[39, 88, 33]]\). The answer should let you know you did a good job.
Recall that given a set of vectors $S=\{\vec v_1, \vec v_2,\ldots, \vec v_k\}$, a linear combination of these vectors was a sum of the form $$c_1\vec v_1+c_2\vec v_2+\cdots+c_k\vec v_k.$$ The span of a set of vectors is the set of all linear combinations of the vectors. In linear algebra we took a small set of vectors and spanned the vectors to create vector spaces. We defined the span of $S$ to be the set of all linear combinations of vectors in $S$.
Given a permutation, we've shown that we can use function composition to create new permutations. If $S$ is a set of permutations on $X$, we'd like to have a way to talk about combining the permutations. Instead of multiplying by a scalar and adding, we'll decide how many times to repeatedly apply the function, and then compose different functions together.
Definition (Composition Combination Of Permutations)
Let $X$ be a set, and $S$ be a set of permutations of $X$.
- If $\sigma$ is a permutation of $X$, we'll use exponential notation to express repeated composition of $\sigma$. This gives us $\sigma^2=\sigma\circ \sigma$ and $\sigma^5=\sigma\circ\sigma\circ\sigma\circ\sigma\circ\sigma$, etc.
- We'll use negative exponents when we want to repeated apply an inverse, which gives us $\sigma^{-n}=\left(\sigma^{-1}\right)^n$.
- A composition combination of permutations in $S$ is a composition of the form $$\sigma_1^{n_1}\circ\sigma_2^{n_2}\circ\cdots\circ \sigma_k^{n_k},$$ where $k\in\mathbb{N}$, each $\sigma_i\in S$, and each $n_i\in \mathbb{Z}$ for $i\in \{1,2,3,\ldots,k\}$.
- The span of $S$, written $\text{span}(S)$ is the set of all composition combinations of permutations in $S$. We'll say that the set $S$ generates $\text{span}(S)$.
As an example, if $S=\{a,b,c,d\}$ is a set of permutations of $X$, then the composition $a^2\circ b^{-1}\circ c^3$ is a composition combination of permutations in $S$, and so are $d^{-3}$, $b^5\circ a^{-2}$, and more.
Problem 13 (Simple Shift Repetition Game)
Consider the set of simple shift permutations $H=\{\phi_n\mid n\in \mathbb{Z}\}$ on a 26 letter alphabet. We've shown that there are 26 different functions in this set. Consider the following game.
- The first player picks an element $\sigma_1\in H$. They then remove from $H$ the span of $\sigma_1$ (so everything generated by $\{\sigma_1\}$).
- The second player now chooses an element $\sigma_2\in H$ that hasn't yet been removed. They then remove from $H$ any element in the span of $\{\sigma_1,\sigma_2\}$. At this stage, any permutation that can be written as a composition combination of the permutations $\sigma_1$ and $\sigma_2$ has been removed.
- Players alternate taking turns, choosing an element $\sigma_k\in H$ that hasn't been removed in a previous stage, and then removing from $H$ any element in the span of $\{\sigma_1,\sigma_2,\ldots,\sigma_k\}$.
- Whoever take the last element of $H$ wins. The game can also be played as a misere game.
Answer the following questions.
- Player 1 takes $\phi_6$. Which elements should be removed from $H$
- Is there a way for player 1 to win on the first move? Explain.
- What's the largest number of turns that can occur in this game (so if neither player tries to win, how long can the game go on)?
- If we play this as a misere game, does player 1 have a winning strategy?
Problem 14(The Span Of A Simple Shift)
Suppose that our alphabet $S$ consists of only 12 letters $S=\{a,b,c,d,e,f,g,h,i,j,k,l\}$. Let $H_{12}=\{\phi_n\mid n\in \mathbb{Z}\}$ be the set of simple shift permutations on this 12 letter alphabet (we wrap around from $l$ to $a$).
- For each $n\in \{0,1,2,\ldots,11\}$, list the elements in $\text{span}(\{\phi_n\} ) $.
- For which $n$ does $\text{span}(\{\phi_n\})=H_{12}$.
- Make a conjecture about any patterns you see above and their relation to the size (12) of the alphabet.
- Whenever you make a conjecture, you should always test your conjecture on an example you have not yet considered. Pick another integer $k\neq 12,26$, and look at the set $H_k$ of simple shift permutations of an alphabet consisting of $k$ letters. Then check if your conjecture holds.
Much of our work up to this point has been based on the ability to compute a remainder. This is all based on the Division Algorithm.
Theorem (Division Algorithm)
Let $a,n\in\mathbb{Z}$, with $n> 0$. Then there exists unique integers $q$ and $r$ (called the quotient and remainder) such that $a=qn+r$ where $0\leq r<n$.
Problem 15(Division Algorithm Proof)
Prove the Division algorithm.
One of our main uses of the division algorithm is modular arithmetic.
Definition (Modular Arithmetic)
Let $a,b,n\in \mathbb{Z}$ with $n>0$. We say that two integers $a$ and $b$ are congruent mod $n$, and write $a \mod n= b\mod n$, if they have the same remainder after dividing by $n$. If $a=qn+r$ where $r$ is the remainder after dividing by $n$, then we'll often write $r=a\mod n$. There are lots of ways to denote this in the literature. We might say $r\equiv a\mod n$, $r=a\pmod n$, $a\mod n \equiv b \mod n$, and more.
Problem 16(Remainders Equal Iff Difference Is A Multiple)
Let $a,b,n\in\mathbb{Z}$ with $n>0$. Prove that $a\pmod n = b \pmod n$ if and only if $a-b$ is a multiple of $n$.
Many encryption algorithms depend entirely on modular arithmetic. The RSA public key encryption algorithm requires that we compute extremely large powers of rather large numbers. For example, we might need to compute $2348971^{986871578457358918334698187}$. This can be an expensive operation, unless we find some patterns to help us. The next problem provides a beginning at doing this.
Problem 17(Computing Powers Modn Conjecture)
We need to be able to compute $a^k\pmod n$.
- Compute $2^k\pmod 5$ for $k=1,2,3,4,5,6,7$. What pattern do you see. What is $2^k\pmod 5 $ for $k=257$ and for $k=49827512$.
- Compute $5^k\pmod {11}$ for $k=1,2,3,4,5,6,7,8,9,10,11,12$. Can you discover a pattern. What if $k=3047$ or $k=478209183234$?
- Make a conjecture about $a^k\pmod n$. Come up with a different example to back your conjecture.
We need a common notation to talk about permutations. If $\sigma$ is a permutation of $X=\{1,2,3,4,5,6\}$, then we could use the matrix notation $ \sigma= \begin{bmatrix}1&2&3&4&5&6\\2&4&6&1&5&3\end{bmatrix} $ to represent the permutation $$ \sigma(1)=2,\sigma(2)=4,\sigma(3)=6,\sigma(4)=1,\sigma(5)=5,\sigma(6)=3 $$ Alternately, we could look at cycling patterns that occur in the permutation and write $1\to 2\to 4\to 1$ and then stop because at this point the cycle repeats. We'd also need to write $3\to 6\to 3$ and $5\to 5$, though if we left the $5\to 5$ part off we could assume that 5 did not change. Rather than writing the arrows, we'll represent this permutation by writing $\sigma=(1,2,4)(3,6)(5)$, or leaving off the fact that 5 maps to itself we could just write $\sigma=(1,2,4)(3,6)$. We can use this notation to express any permutation. We need a formal definition for this cycle notation. You can read more about disjoint cycle notation on page 98 in Gallian's Contemporary Abstract Algebra.
Definition (Disjoint Cycle Notation)
Let $X=\{1,2,3,\ldots ,n\}$ for some positive integer $n$. Let $\sigma$ be a permutation which we have written in the matrix form $ \sigma= \begin{bmatrix}1&2&\cdots&n\\\sigma(1)&\sigma(2)&\cdots&\sigma(n)\end{bmatrix}. $ Let $a_1\in X$ (often we choose $a_1=1)$ and then compute $\sigma(a_1),\sigma^2(a_1),\sigma^3(a_n),\ldots, \sigma^{k_1}(a_n)$ until the next application of $\sigma$ returns $a_1$. This gives the first cycle (vector) $\alpha_1=(a_1,\sigma(a_1),\ldots,\sigma^{k_1}(a_1))$. We then pick $a_2\in X$ so that $a_2$ is not an entry in $\alpha_1$, and repeat this process to obtain a second cycle $\alpha_2=(a_2,\sigma(a_2),\sigma^2(a_2),\ldots,\sigma^{k_2}(a_2))$. We then pick $a_3\in X$ so that $a_3$ is not an entry in $\alpha_1$ nor $\alpha_2$, and repeat the process to obtain the cycle $\alpha_3$. At each stage we pick a new element $a_k\in X$ that is not an entry in any of $\alpha_1,\alpha_2,\ldots, \alpha_{k-1}$, and then repeatedly apply $\sigma$ to obtain the cycle $a_k$. The process stops when every element of $X$ is in $\alpha_k$ for some $k$. We then write $$\sigma=\alpha_1\circ\alpha_2\circ\cdots \circ \alpha_m = \alpha_1\alpha_2\cdots\alpha_m$$ where $m$ is the number of cycles needed to represent the permutation. Whether we include the composition symbol or not is a matter of preference.
We will often omit writing singleton vectors $(a)$. So if $X=\{1,2,3,4\}$, then instead of writing $(1)(2,3)(4)$, we'll just write $(2,3)$. The permutation $(2,3)$ does not change the elements $1$ and $4$, so we omit writing them. The identity permutation would be $(1)(2)(3)(4)$. We could omit all singletons which would leave us with nothing, so in this case we'll write $()$ to represent the identity permutation.
Problem 18(Disjoint Cycle Notation Practice With Automorphisms Of A Square)
We have already shown that there are 8 automorphisms of the graph below.

Write each of these automorphism using disjoint cycle notation. As an example, the automorphism that leaves 1 and 3 unchanged, but swaps 2 and 4, we write as $(1)(2,4)(3)$.
Problem 19(Automorphisms On Several Graphs With 4 Vertices)
Consider the two graphs below.
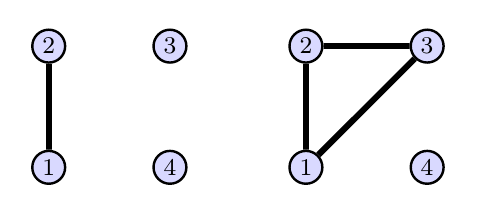
- For each graph, list the automorphisms of the graph. Use disjoint cycle notation to represent each automorphism.
- For each automorphism, state the smallest positive value of $k$ for which $\sigma^k$ is the identity automorphism. This is called the order of the automorphism.
- Construct another graph on 4 vertices different than the three we have seen so far. How many automorphisms does this graph have? Explain.
Exercise (The Product Of The GCD And LCM)
Prove that for positive integers $m$ and $n$, we always have $mn=\gcd(m,n)\text{lcm}(m,n)$, in other words the product of the greatest common divisor and least common multiple of two natural numbers is always the same as their product.
Click to see a solution.
One way to prove this theorem is to use the factorization of each number into a product of primes. Some people call this the fundamental theorem of arithmetic, namely that each number can be written uniquely (up to reordering) as a product of prime numbers. As the proof follows directly from an example, let's look at one example.
Suppose $n=50=2^1\cdot3^0\cdot 5^2$ and $m=120 = 2^3\cdot 3^1 \cdot 5^1$. We list $3^0$ in the factorization of $n$ because this helps us see a general pattern. Since 2 appears once in the first number, and three times in the second, the greatest common divisor has one 2 in its factorization (the minimum of the powers 1 and 3). Also, any common multiple includes all three copies of 2 in its factorization (the maximum of the powers 1 and 3). Repeating this with each prime, we see that $\gcd(n,m) = 2^{\min\{1,3\}}\cdot 3^{\min\{0,1\}}\cdot 5^{\min\{2,1\}}$, and $\text{lcm}(m,n) = 2^{\max\{1,3\}}\cdot 3^{\max\{0,1\}}\cdot 5^{\max\{2,1\}}$. Since the sum of two numbers is equal to the sum of their minimum and maximum, the fact that $nm = \gcd(n,m)\text{lcm}(n,m)$ follows by using the commutative property of addition to rearrange the products of primes, as in $$\begin{align} nm &= \left(2^1\cdot3^0\cdot 5^2\right)\left(2^3\cdot 3^1 \cdot 5^1\right) \\ &= \underbrace{\left(2^1\cdot3^0\cdot 5^1\right)}_{\text{min exponents}}\underbrace{\left(2^3\cdot 3^1 \cdot 5^2\right)}_{\text{max exponents}} \\&= \gcd(n,m)\text{lcm}(n,m).\end{align}$$
The proof for general integers is similar. Suppose $n$ and $m$ are integers. After writing each number as a prime factorization, suppose that the distinct primes that appear in either integers are $p_1,p_2,\ldots, p_k$. We then write $n=p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}$ and $m=p_1^{b_1}p_2^{b_2}\cdots p_k^{b_k}$. We then compute $$\begin{align} nm &= \left(p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}\right) \left(p_1^{b_1}p_2^{b_2}\cdots p_k^{b_k}\right) \\ &= \underbrace{\left(p_1^{\min\{a_1,b_1\}}p_2^{\min\{a_2,b_2\}}\cdots p_k^{\min\{a_k,b_k\}}\right)}_{\text{min exponents}}\underbrace{\left(p_1^{\max\{a_1,b_1\}}p_2^{\max\{a_2,b_2\}}\cdots p_k^{\max\{a_k,b_k\}}\right)}_{\text{max exponents}} \\ &= \gcd(n,m)\text{lcm}(n,m). \end{align}$$
Definition (The Order Of A Permutation)
The order of a permutation $\sigma$ is the smallest positive integer $n$ such that $\sigma^n$ equals the identity permutation.
Definition (The Game of Permutation Scoring also called Generate/Don't Generate)
Just as in the Simple Shift Repetition Game, we can play a similar game with any set of permutations of the same set $X$. Let $H$ be a set of permutations of a set $X$. We'll generally assume that the set $X$ is finite so that the game is guaranteed to end. However, you can play this game with an infinite set $X$.
Here are the rules.
- The first player picks an element $\sigma_1\in H$. They then remove from $H$ the span of $\{\sigma_1\}$ (so everything generated by $\sigma_1$).
- The second player now chooses an element $\sigma_2\in H$ that hasn't yet been removed. They then remove from $H$ any element in the span of $\{\sigma_1,\sigma_2\}$. At this stage, any permutation that can be written as a composition combination of the permutations $\sigma_1$ and $\sigma_2$ has been removed.
- Players alternate taking turns, choosing an element $\sigma_k\in H$ that hasn't been removed in a previous stage, and then removing from $H$ any element in the span of $\{\sigma_1,\sigma_2,\ldots,\sigma_k\}$.
- Whoever takes the last element of $H$ wins.
There are several variations:
- The game can also be played as a misere game, where whoever takes the last element of $H$ wins.
- You win by taking the last element. However, you cannot take the last element unless there are no other legal choices. So you can't try to win, rather you must be forced to win.
Problem 20(The Game Of Permutation Scoring On A Square)
Let's play the game of scoring on the automorphism group of the square. We know there are 8 automorphism. Play this game a few times to get a feel for what different choices will give.
- Show there is no way for player 1 to win on the first move.
- If player 1 takes any of the flips for their first move, what should player 2 choose to win the game?
- Does player 1 have a winning strategy? What is it?
It would be nice if we could create a way to visually keeping track of which elements of $H$ have been taken. Let me describe how we can do this with an example. Suppose you are playing the game on a square (as above). Player one takes the permutation $(1,2,3,4)$. Then player $2$ chooses the element $(1,2)(3,4)$. Here's how we make the graph.
- Each element in $H$ will represent a vertex.
- When player 1 chooses $(1,2,3,4)$, pick a color (I'll choose red) and then draw a red arrow from each permutation $\sigma\in H$ to the permutation $(1,2,3,4)\circ \sigma$. In other words, we're going to draw a graph that shows what happens if we apply the automorphism $(1,2,3,4)$ after doing any other automorphism. If we start at the identity permutation $()=(1)(2)(3)(4)$, then we have $(1,2,3,4)\circ ()=(1,2,3,4)$, so we draw a red arrow from $()$ to $(1,2,3,4)$. Similarly, starting at $(1,2,3,4)$ we draw an arrow to $(1,2,3,4)\circ(1,2,3,4)=(1,3)(2,4)$. Continuing in this fashion for each permutation gives us the graph below, with two red cycles of 4.
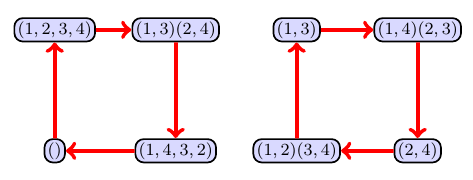
- The elements that are removed after choosing $(1,2,3,4)$ are any elements that we can get to by following a path that contains $(1,2,3,4)$. These are the 4 automorphisms in the cycle on the left.
- Now player 2 chooses $(1,2)(3,4)$. We now use a different color (I chose blue in the example below), and then at each vertex draw an arrow starting at $\sigma\in H$ and ending at $(1,2)(3,4)\circ \sigma$. The tricky part is finding a nice way to draw the graph without to many edge crossings (do you see how the outer circle flipped directions). Both of the examples below are ways to represent this graph. We can use an edge with an arrow on each end to illustrate that there is an arrow going both ways.
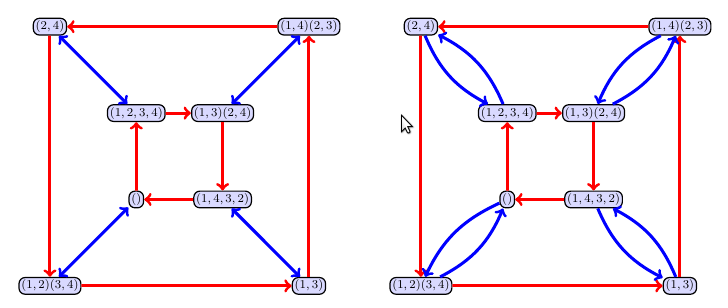
- The arrows in the graph above represent composition by either $(1,2,3,4)$ or $(1,2)(3,4)$. If you start at $(1,3)$ and want to compute $(1,2,3,4)\circ(1,2)(3,4)\circ(1,3)$, then you just have to start at $(1,3)$, follow the blue arrow to get to $(1,2)(3,4)\circ(1,3)=(1,4,3,2)$, and then follow the red arrow to get to $(1,2,3,4)\circ(1,4,3,2)$.
The mathematical program Sage can also help with the computations. The command PermutationGroup() below creates the span of the permutations listed. The command cayley_graph() creates the graph described above, but only shows the part of the graph that contains the permutations listed. Try executing the block of code below.
g1 = PermutationGroup(["(1,2,3,4)"]) #The set g1 is the span of the permutations listed. d1=g1.cayley_graph() #This creates the Cayley graph of the g1. d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) #This shows the Cayley graph. print(g1.list()) #This print a list of the elements in g1. g2 = PermutationGroup(["(1,2,3,4)", "(1,2)(3,4)"]) d2=g2.cayley_graph() d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) print(g2.list())
Problem 21 (Composing Permutations Using Disjoint Cycle Notation)
Let $R_{90}=(1,2,3,4)$ and $H=(1,2)(3,4)$.
- Express the compositions $R_{90}\circ H$ and $H\circ R_{90}$ in cycle notation. Be prepared to explain how you computed this.
- Express the compositions $R_{90}\circ (1,3)$ and $H\circ (1,3)$ in cycle notation. Can you see these products in the graph above?
- Express the composition $(1,2,4)\circ (1,4)(2,3)\circ (2,4)$ in cycle notation. Note that $(1,2,4)$ is not an automorphism of the square, but is a permutation.
- Evalute the Sage command below. In the second graph below you should see that starting at $()$ and following the colored arrows corresponding to $(2,4)$ and then $(1,4)(2,3)$ gets you to the element $(1,4,3,2)$ which is precisely the composition $(1,4)(2,3)\circ (2,4)$. In the third graph below, if you start at the identity $()$ and the follow the colored arrow corresponding to $ (2,4)$, and then $(1,4)(2,3)$, and then $(1,2,4)$, you should end up at the same spot as you did in part 3. Click evaluate again if the graph you have is hard to read (as the graph will redraw).
g1 = PermutationGroup(["(2,4)"]) #The set g1 is the span of the permutations listed. d1=g1.cayley_graph() #This creates the Cayley graph of the g1. d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) #This shows the Cayley graph. print(g1.list()) #This print a list of the elements in g1. g2 = PermutationGroup(["(2,4)","(1,4)(2,3)"]) d2=g2.cayley_graph() d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) print(g2.list()) g3 = PermutationGroup(["(2,4)","(1,4)(2,3)", "(1,2,4)"]) d3=g3.cayley_graph() d3.show(color_by_label=True, vertex_size=0.03, vertex_labels=True,figsize=8) print(g3.list())
Problem 22 (Creating Cayley Graphs Of Simple Shift Permutations)
Let's make some Cayley graphs as they relate with the game of Scoring on simple shift permutations. To get Sage to make the graphs, you'll first have to write the simple shift permutation in disjoint cycle notation. As an example, if there are 6 letters in our alphabet $X=\{1,2,3,4,5,6\}$, then we could write the simple shift $\phi_2$ as $(2,4,6)(1,3,5)$. If player 1 chooses $\sigma_1=\phi_2$ and player 2 chooses $\sigma_2=\phi_3$, then the following Sage code visually provides a graph of $\text{span}(\{\sigma_1\})$ and then $\text{span}(\{\sigma_1,\sigma_2\})$.
g1 = PermutationGroup(["(2,4,6)(1,3,5)"]) d1=g1.cayley_graph() d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) print(g1.list()) g2 = PermutationGroup(["(2,4,6)(1,3,5)","(1,4)(2,5)(3,6)"]) d2=g2.cayley_graph() d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) print(g2.list())
By hand, my first graph would contain two unconnected triangles. My second graph would look similar to the graph above.
- Suppose the alphabet is $X=\{1,2,3,4,5,6\}$. Player 1 chooses $\phi_1$. Draw the associated graph.
- Suppose the alphabet is $X=\{1,2,\ldots,10\}$. Player 1 chooses $\phi_5$. Player 2 chooses $\phi_4$. Draw the two associated graphs.
- Suppose the alphabet is $X=\{1,2,\ldots,12\}$. Player 1 chooses $\phi_5$. Draw the associated graph.
- Suppose the alphabet is $X=\{1,2,\ldots,12\}$. Player 1 chooses $\phi_6$. Player 2 chooses $\phi_2$. Player 1 then chooses $\phi_3$. Draw the three associated graphs. The first graph should consist of 6 arrows between pairs of vertices (Sage will only show you the segment connnecting $()$ and $\phi_6$). Your second graph should have 2 hexagons with arrows crossing in the middle. The last graph should connect the edges of the hexagons.
Here's a blank Sage cell that you can use to perform some computations. You'll probably want to copy code from above and make some changes.
When we create graphs with Sage, it always creates a graph of the span of the permutations given. These graphs have a lot of really nice symmetry properties, and these properties are central to abstract algebra.
Problem 23 (Permutation Scoring On S 3)
Consider the game of permutation scoring on the set $S_3$, where $S_3$ represents the set of all permutations of $X=\{1,2,3\}$. We already know that there are 6 elements in $S_3$.
- Play the game of permutation scoring on $S_3$. Play it a few times.
- Can player 1 win by choosing a single permutation in $S_3$?
- Does player $1$ have a winning strategy? What is it?
- Pick an element in $S_3$ other than the identity, and call it $\sigma$. Let $S=\text{span}(\sigma)$. What is the span of $S$?
- Repeat part 4 with a different element of $S_3$. You can use Sage to make this part fast (first compute the span of $\sigma$ with Sage. The list below the graph gives you the elements of the span. Then create a graph using these elements.
- Make a conjecture.
Definition (A Closed Set Of Permutations)
We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.
Problem 24 (The Span Of A Set Of Permutations Is Closed)
Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.
We'll be using modular arithmetic in a lot of things that we do throughout the semester. Let's invent a notation to help us talk about modular arithmetic.
Definition (The Set ZN Of Integers Mod N)
For each positive integer $n$, let $\mathbb{Z}_n=\{0,1,2,\ldots, n-1\}$ which is the same as $\mathbb{Z}_n = \{k\mod n\mid k\in \mathbb{Z}\}$. This is just the set of remainders when dividing by $n$. We'll refer to them as the integers modulo $n$, or the integers mod $n$.
Question
Take a look at the last question of The Set Of Simple Shift Permutations. Does this definition look familiar?
In previous problems, we've been using without proof some facts about modular arithmetic, namely that we can perform addition and subtraction either before or after we compute a remainder. Let's prove this is true.
Problem 25 (Modular Arithmetic Properties)
Let $n$ be a positive integer. Let $a,b\in \mathbb{Z}$.
- Show that $((a \mod n)+(b\mod n))\mod n = (a+b)\mod n$. In other words, show that the sum of the remainders has the same remainder as the original sum.
- Show that $((a \mod n)(b\mod n))\mod n = (ab)\mod n$. In other words, show that the product of the remainders has the same remainder as the original product.
Remember, you'll want to use the division algorithm to obtain quotient and remainders when dividing $a$, $b$, $ab$, and $a+b$ by $n$. You'll need to use the problem, Remainders Equal Iff Difference Is A Multiple, to complete your work.
Problem 26 (Powers With Modular Arithmetic)
- We know that $481\mod {483} =(-2)\mod {483}$. Use this fact to quickly compute $481^2\mod{483}$ without a calculator. [How can you use the $-2$ to simplify this?]
- Using the same idea, what is $481^{3}\mod{483}$ and $481^4\mod{483}$? You should be giving a positive integer less than 483 for all your answers.
- Explain why $12\cdot 16 \mod 17$ is the same as $(-5)(-1)\mod 17$.
- Now compute $14^k \pmod {17}$ without a calculator for as many values of $k$ as needed until you find a repeating pattern. See the hint below.
Let me give you a suggestion. Rather than trying to compute $14^4$, instead first compute $14^2$ by considering $(-3)^2$. To compute $(14)^3$, instead use the product $(14)^2(14)=(9)(-3)=(-8)(-3)$. Use your work from the previous power to figure out the next power. If you try to do this with brute force, it gets outrageously large really fast. If you swap from positive to negative values when the numbers get large (above 8), you should be able to do this without ever needing long division. You should find that no product ever gets above 24.
The following Sage code will compute powers with modular arithmetic. You are welcome to check your answers with this, but the whole point to the problem is to learn how to simplify the computations by hand. To compute $a^m\mod n$ you would write "power_mod($a$,$m$,$n$)."
power_mod(481, 4, 483)
Problem 27 (Matrix Encryption Mod 5)
In the Problem (Simple Matrix Encryption), we took a plain text message written in columns of a matrix $M$ and a matrix $A$ and used the product $AM$ to encode a message. Let's now combine matrix encryption with modular arithmetic to obtain a new encryption scheme. Once we have done this, we'll be one step closer to understanding modern encryption techniques. To simplify our work, let's use a small alphabet consisting of 5 letters. Instead of using the set $S=\{a,b,c,d,e\}$, let's just use numbers for our letters and we'll consider the alphabet $S=\{0,1,2,3,4\}=\mathbb{Z}_5$. Given the plain text "bad bed" or "10 31 43", we can encode it in the columns of the matrix $$M=\begin{bmatrix}1&3&4\\0&1&3\end{bmatrix}.$$ An 2 by 2 encryption key using coefficients mod 5 is a 2 by 2 matrix $A=\begin{bmatrix}a&b\\c&d\end{bmatrix}$ where $a,b,c,d\in \mathbb{Z}_5$. Here are the steps to our encryption scheme.
- First convert the plain text to a matrix $M$ where the letters are place in the matrix top to bottom, column by column.
- Take the encryption key $A$ and compute the product $AM$.
- Reduce all the entries in $AM$ mod 5. So the cipher text only consists of the numbers in $\mathbb{Z}_5$.
Answer the following questions.
- Suppose we let $A=\begin{bmatrix}4&2\\1&3\end{bmatrix}$. Why is this matrix not suitable as an encryption key? (Hint: what is the determinant, and why is that a problem?)
- Suppose we let $A=\begin{bmatrix}2&1\\4&3\end{bmatrix}$. The inverse of $A$ if we ignore modular arithmetic is $\frac{1}{2}\begin{bmatrix}3&-1\\-4&2\end{bmatrix}$. We know that we can replace $-4$ with $1$ when working modular 5. Similarly we can replace $-1$ with a positive number. We need to find the multiplicative inverse of 2 when working modular 5. Find a value $b\in \mathbb{Z}_5$ so that $2b\mod 5=1$. This number $b$ is the inverse of $2$ modular 5.
- State a matrix $B$ with coefficients in $\mathbb{Z}_5$ so that $AB$ is the identity matrix after reducing each entry mod 5. Actually perform the product by hand, and show how this matrix product reduces to the identity.
Definition (Modular Multiplicative Inverse and $U(n)$)
Let $n$ be a positive integer, and let $a\in \mathbb{Z}_n$. Then the modular multiplicative inverse of $a \mod n$ is an integer $b\in \mathbb{Z}_n$ such that $(ab)\mod n=1$. If such an integer exists, then we'll write $a^{-1}\mod n$ to represent the modular multiplicative inverse. If the context is clear, we may just refer to this as the inverse instead of the modular multiplicative inverse. We'll use the notation $U(n)$ to represent the set of elements in $\mathbb{Z}$ that have a modular multiplicative inverse. Notationaly, we write $$U(n)=\{a\in\mathbb{Z}_n\mid \text{ there exists } b\in \mathbb{Z}_n \text{ such that } (ab)\mod n=1\}.$$
The Sage code "inverse_mod(a,n)" will compute the modular multiplicative inverse of $a\mod n$ or return an error.
inverse_mod(7, 11)
Problem 28 (Computing Multiplicative Inverses For Small N)
To use modular arithmetic in matrix encryption, we must be able to find the modular multiplicative inverse of $a \mod n$. For each $n\leq 13$ and $a\in \mathbb{Z}_n$, we now compute the inverse of $a\mod n$ or explain why it does not have one.
- Why does $0\mod n$ never have an inverse?
- What is the multiplicative inverse of $1\mod n$?
- For $n=3$, what is the multiplicative inverse of $a=2$.
- For $n=4$, show that 2 does not have an inverse by computing $2\cdot 0$, $2\cdot 1$, $2\cdot 2$, and $2\cdot 3$ all modulo $4$. What is $3^{-1}\mod 4$?
- For each $n$ between 5 and 13, create a table that shows the inverse of each $a\in \mathbb{Z}_n$. List the elements of $\mathbb{Z}_n$ along the top row, and beneath each element list the multiplicative inverse, or cross off the number if there is no multiplicative inverse.
When you are done you should have a list of the elements of $U(n)$ for each $n$ up to 13, as well as the inverse of each element in $U(n)$. Do you see any patterns?
For $n=9$, you should obtain a table somewhat similar to the following table.
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $a^{-1}$ | x | 1 | 5 | x | 7 | 2 | x | 4 | 8 |
Definition (Cayley Graph Of A Span Of Permutations)
Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.
Problem 29 (Cayley Graph Patterns)
In each scenario below, you should draw a Cayley graph.
- Let $X=\mathbb{Z}$, an infinite set. Consider the permutation $\phi_1:\mathbb{Z}\to \mathbb{Z}$ defined by $\phi_1(x)=x+1$. This permutation shifts elements in $\mathbb{Z}$ right one, with no wrap around. If we let $S=\{\phi_1\}$, give a rough sketch of the Cayley graph of $\text{span}(S)$. It's a rough sketch of the graph because there are infinitely many vertices.
- How would you change your graph in part 1 if instead you used $S=\{\phi_2,\phi_3\}$, where these are shifts right 2 and 3 respectively?
- Suppose that $X$ is a set, and that $S$ contains a single automorphism $s$ of $X$. Suppose also that we know $s^6$ is the identity (so following the arrow colored $c_s$ 6 times will return us to where we started). Construct a Cayley graph of $\text{span}(S)$. Is there more than one right answer to this?
- Suppose that we know $S$ contains two elements $a$ and $b$. We also know that $a^2$ and $b^4$ are both the identity. In addition, we know that $a\circ b=b\circ a$, so if we start somewhere and follow the arrows colored $c_a$ and then $c_b$, then we should end up at the same place if we followed the arrows colored $c_b$ and then $c_a$. Construct a graph that satisfies these relationships. We'll often write this as $$\left<a,b\mid a^2=id, b^4=id, a\circ b=b\circ a\right>.$$
If $X$ is a set, and $S$ is a set of permutations of $X$, then we can create a Caley graph for the span of $S$. Here's a formal definition.
Definition (Cayley Graph Of A Span Of Permutations)
Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.
We've done this with several automorphism groups of graphs, as well as simple shift permutation groups.
Problem 30 (Cayley Graphs Of Two Automorphism Groups)
Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.

We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).
- For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
- For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.
Sometimes we can create a Cayley graph of a set of automorphisms without even knowing what the sets $X$ or $S$ are. All we need to know is how many automorphisms are in $S$, and some relationships about the automorphisms. The next problem has you examine a few more Cayley graphs.
Problem 31 (Cayley Graphs From Relations)
In each scenario below, you should draw a Cayley graph.
- Suppose that $X$ is a set, and that $S$ contains a single automorphism $s$ of $X$. Suppose also that we know $s^6$ is the identity (so following the arrow colored $c_s$ 6 times will return us to where we started). Construct a Cayley graph of $\text{span}(S)$. Is there more than one right answer to this?
- Suppose that we know $S$ contains two elements $a$ and $b$. We also know that $a^2$ and $b^4$ are both the identity. In addition, we know that $a\circ b=b\circ a$, so if we start somewhere and follow the arrows colored $c_a$ and then $c_b$, then we should end up at the same place if we followed the arrows colored $c_b$ and then $c_a$. Construct a graph that satisfies these relationships. We'll use the notation $$\left<a,b\mid a^2=id, b^4=id, a\circ b=b\circ a\right>$$ to tell us that $S=\{a,b\}$ with the relations listed after the $\mid$.
- Generalize your result above to draw a Cayley graph if instead of $b^4=id$ we have $b^k=id$.
If $X$ is a set, and $S$ is a set of permutations of $X$, then we already know how to create the span of $S$. In general, the span of $S$ will include more permutations than what we started with. However, sometimes we won't be able to obtain any new permutations by spanning $S$. When this happens, we say that the set of permutations is closed (under function composition). Here's a formal definition.
Definition (A Closed Set Of Permutations)
We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.
The next problem has you prove some relationships between a set of permutations $S$ and its span.
Problem 32 (Relationship Between S And Its Span)
Let $S$ be a set of permutations of $X$.
- Prove that $S\subseteq \text{span}(S)$. In other words, we know that $S$ is always contained in its span; the span might be larger.
- Prove that if $\text{span}(S)\subseteq S$, then $S$ is closed.
- If $T\subseteq S$, then show that $\text{span}(T)\subseteq\text{span}(S)$.
Definition (Integer Linear Combination Of Integers)
Let $a_1, a_2, \ldots, a_k$ be $k$ integers.
- An integer linear combination of these integers is an expression of the form $$c_1a_1+c_2 a_2+ \cdots+c_k a_k$$ where each coefficient $c_i$ is an integer.
- The span of the set of integers $\{a_1, a_2, \ldots, a_k\}$ is the set of all possible integer linear combinations of these integers, namely $$\text{span}(\{a_1, a_2, \ldots, a_k\})=\text{span}(a_1, a_2, \ldots, a_k)=\{c_1a_1+c_2 a_2+ \cdots+c_k a_k\mid c_i\in \mathbb{Z} \text{ for }1\leq i\leq k\}.$$ For ease of notation, we'll often leave off the set notation when spanning a set of integers.
- If the set $S$ of integers is infinite, then we still define the span of $S$ to be the set of all integer linear combinations of integers in $S$. Hence we know $x\in S$ if and only if there exists a natural number $k$ such that $x=c_1a_1+c_2 a_2+ \cdots+c_k a_k$ where $a_i\in S$ and $c_i\in \mathbb{Z}$ for $1\leq i\leq k$.
- When there are only two integers, we'll often use $a$ and $b$ as the integers, and $s$ and $t$ as the coefficients. So the set of all integer linear combinations of $a$ and $b$ is $$\text{span}(a,b) = \{sa+tb\mid s,t\in\mathbb{Z}\}.$$
Problem 33 (Integer Linear Combination Practice)
Complete the following.
- Compute the span of $3$, i.e. make a list of the elements in this set. In general, what is the span of a single integer $a$? (We know it by a different name.)
- What is $\text{span}(4,6)$? List the elements. Find a single number $a$ so that $\text{span}(a)=\text{span}(4,6)$.
- What is $\text{span}(4,5)$?
- Let $S=\{a_1,a_2,\ldots,a_k\}$ be a set of integers. Show that if $c\in \text{span}(S)$, then so is every multiple of $c$.
We've seen a lot of relationships in class about modular arithmetic, inverses mod $n$, simple shift encryption schemes, and more. The next problem makes a connection between some of these. We'll connect it to even more next time.
Problem 34 (When Does An Integer Have A Modular Multiplicative Inverse)
Let $a$ and $n$ be integers, with $n>1$. Show that the following are equivalent.
- The integer $a$ has a multiplicative inverse mod $n$
- We have $1\in \text{span}(a,n)$. In other words, we can write 1 as a linear combination of $a$ and $n$.
- We have $\text{span}(a,n)=\mathbb{Z}$. Remember that $\text{span}(a,n) = \{sa+tn\mid s,t\in\mathbb{Z}\}.$
Remember, to show that three things are equivalent you must show that each implies the other. One way to do this is show that 1 implies 2, then show that 2 implies 3, and then show that 3 implies 1. Then each implies the other.
The two problems above, together with much of our work from the previous weeks, leads us to one of the biggest theorems in number theory. We'll prove this theorem later in the semester.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Corollary (When Are Two Numbers Relatively Prime)
Two nonzero numbers $a$ and $b$ are relatively prime (i.e. their greatest common divisor is 1) if and only if there exists $s$ and $t$ such that $sa+tb=1$.
Problem 35 (Connecting Multiples And Spans Of Integers)
Suppose that $a$ and $b$ are integers.
- Prove that if $a$ is a multiple of $b$, then we must have $\text{span}(a)\subseteq\text{span}(b)$.
- Is the converse of the statement above true or false? Make sure you prove your result.
Problem 36 (Permutations of $U(n)$)
Suppose $n$ is an integer greater than 1 and let $X=U(n)$, so the set of integers mod $n$ that have a multiplicative inverse mod $n$. For each $a\in U(n)$, we can define a permutation of $U(n)$ by $f_a(x)=xa\pmod n$ for each $x\in U(n)$. This problem asks you to show that this is indeed a permutation of $U(n)$. This requires that you show the following:
- For each integer $n\geq 2$, show that if $a\in U(n)$ and $x\in U(n)$, then the product $f_a(x)=xa\pmod n\in U(n)$. This shows that $f_a:U(n)\to U(n)$ is a map from $U(n)$ to $U(n)$.
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is one-to-one. (As a reminder, one-to-one means that if $f_a(x)=f_a(y)$, then $x=y$.)
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is onto. (As a reminder, onto means that if $y\in U(n)$, then there exists $x\in U(n)$ such that $f_a(x)=y$.)
For part 2, you'll need to show that if $ax\pmod n=ay\pmod n$, then $x=y$. Here's a hint that should help you throughout the entire semester. Ask yourself, "How would I solve this if we were just working with the integers and we needed to show $ax=ay$ implies $x=y$?" Remove the word divide from your vocabulary, and replace it with "multiply by the inverse."
Problem (Bonus) (The Point Group Of A Cube)
Consider a cube with vertices located at the 8 points $(\pm 1, 1,1)$, $(\pm 1, 1,-1)$, $(\pm 1, -1,1)$, $(\pm 1, -1,-1)$, and edges that connect each vertex to the three nearest points. For example, vertex $(1,1,1)$ has three edges, one connecting to each of $(1,1,-1)$, $(1,-1,1)$, and $(-1,1,1)$. We can view this as a graph whose vertices are these 8 points, along with the 12 edges. We will let $O_h$ represent the set of automorphisms of the graph of the cube.
- How many elements are in $O_h$? Explain.
- We will say that a set $S$ of permutations of $X$ is independent if for each $s\in S$, we have $\span (S\setminus\{s\})\neq \span (S)$. In other words, every element in $S$ is not in the span of the other permutations in $S$. Find an independent set $S$ of elements in $O_h$ so that $\span(S) = O_h$.
- Use sage to draw the Cayley graph of $O_h$ using S. In addition show the Cayley graph of $O_h$ using $S\setminus\{s\}$ for each $s\in S$. The code provided below can do this for you, by adding and/or removing elements from $S$.
- Challenge: Find another set $S_2$ with a different number of elements than $S$, so that $S_2$ is also an independent set whose span is $O_h$.
S = ["(1,2,3,4)(5,6,7,8)","(1,5,8,4)(2,6,7,3)"]
g = PermutationGroup(S)
d = g.cayley_graph()
print("There are " + str(order(g)) + " elements in the graph below.")
#To see a readable list of the elements, uncomment the line below.
#print(g.list())
d.show(color_by_label=True, vertex_size=0.03, vertex_labels=True)
#We now make a graph of what happens if we remove one element.
for s in S:
T=S[:]; #This makes a copy of S
T.remove(s); #from which we remove s without affecting S.
gT=PermutationGroup(T)
print("Removing " + s + " yields " + str(order(gT)) + " elements.")
gT.cayley_graph().show(color_by_label=True, vertex_size=0.03, vertex_labels=True)
#The graph you create may be difficult to read in 2D.
#Uncomment the next line to see a 3D Cayley graph. Note, it may cause your browser to hang for a moment.
#d.show3d(color_by_label=True, vertex_size=0.03, vertex_labels=False)
For information on this group, see Wikipedia.
Problem 37 (Three Similar Cayley Graphs From Different Contexts)
This problem asks you to draw 3 Cayley graphs. Each Cayley graph should only have 4 vertices.
- Draw a Cayley graph for the set $H_4$ of simple shift permutations of $X=\{1,2,3,4\}$ using the generating set $S=\{\phi_1\}$.
- Then draw a Cayley graph for the span of the permutation $(1,4,3,2)$, which we wrote in disjoint cycle notation.
- Then draw a Cayley graph for $\{f_a\mid a\in U(5)\}$ using the generating set $S=\{f_2\}$. Remember that $f_a$ is a permutation of $U(5)$ defined by $f_a(x)=xa\pmod 5$.
- What do you notice about these Cayley graphs?
The three graphs from the previous problem look very similar, so much so that we could obtain one from the other if we just relabeled the vertex sets. This suggests that in some sense these graphs are the same. We now introduce a formal way to talk about when two graphs are the same.
Definition (Isomorphic Graphs)
Let $G$ and $H$ be two graphs, where we use $V(G)$ and $V(H)$ to denote the vertex sets. A function $f:V(G)\to V(H)$ is called an isomorphism of graphs $G$ and $H$ if $f$ is a bijection and $\{x,y\}$ is an edge of $G$ if and only if $\{f(x),f(y)\}$ is an edge of $H$ (see Wikipedia).
- We call this function $f$ an isomorphism because it "preserves the edge structure" in the graph. In general the word isomorphism refers to a bijection that preserves some kind of structure.
- If there exists an isomorphism of graphs between $G$ and $H$, then we say that $G$ and $H$ are isomorphic.
- If $G$ and $H$ are directed graphs, then an isomorphism of directed graphs would preserve the arrow structure.
- If the directed graphs $G$ and $H$ are colored, then an isomorphism also preserves the color structure, in the sense that $(a,b)$ and $(c,d)$ share the same color if and only if $(f(a),f(b))$ and $(f(c),f(d))$ share the same color.
Problem 38 (Introduction To Cayley Graph Isomorphisms)
Let $H_6 = \{\phi_0,\phi_1,\ldots,\phi_5\}$ be the set of simple shift permutations on an alphabet with 6 letters. Let $K=\{f_a\mid a\in U(7)\}$ be the set of permutations $f_a:U(7)\to U(7)$ defined by $f_a(x)=xa\pmod 7$. Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_1\}$. Then draw the Cayley graph of $K$ generated by $\{f_3\}$. Finally show that the function $g:H_6\to K$ defined by $$ g(\phi_0)=f_1, g(\phi_1)=f_3, g(\phi_2)=f_2, g(\phi_3)=f_6, g(\phi_4)=f_4, g(\phi_5)=f_5, $$ is an isomorphism of Cayley graphs.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_2, \phi_3\}$. Then draw the Cayley graph of $K$ generated by $\{f_2,f_6\}$. Do you believe these two Cayley graphs are isomorphic? You can just give a heuristic argument, rather than a formal proof.
- Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$. We've already shown this set has 6 permutations. Draw a Cayley graph of $S_3$ generated by the permutations $(1,2,3)$ and $(1,2)$. Do you think that this Cayley graph is isomorphic to any of the Cayley graphs above? Why?
Definition (Binary Operation)
Let $G$ be a set. A binary operation on $G$ is a way of combining two elements of $G$ to obtain a new element in $G$. Formally, we just say that a binary operation $*$ is function $*:G\times G\to G$, and we use the notation $a*b$ to represent the function notation $*(a,b)$.
You've been using binary operations your whole life.
Problem 39 (Binary Operation Introduction)
In which of the following scenarios do we have a binary operation on a set $G$. Justify your answers.
- Addition $a+b$ of integers.
- Multiplication $A\cdot B$ of 3 by 3 matrices.
- The dot product $\vec u\cdot \vec v$ of two dimensional vectors.
- The cross product $\vec u\times \vec v$ of three dimensional vectors.
- The scalar product $c\cdot \vec v$.
- Composition $f\circ g$ of permutations on the same set $X$.
- Composition $f\circ g$ of functions from $X$ to $Y$.
Up to this point in the semester, we've been focusing solely on sets of permutations. Every element was a function, which often required keeping track of a bunch of information that wasn't necessary. Spanning a set of permutations gave us closed sets of permutations. We found that there are 4 key properties of a set of closed permutations. Let's now drop the requirement that we have permutations, and instead focus on sets, together with a binary operation, that satisfy these 4 properties. We call a set with these properties a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
We've already seen many groups throughout the semester. Since the span of any set of permutations is closed, then every time we span a set of permutations, we end up with a group. All of the patterns you have discovered about simple shift permutations, automorphisms of graphs, and more, we will be able to transfer to your understanding of abstract groups. Let's look an example, namely a group of matrices that we used before to encrypt messages.
Problem 40 (General Linear Group Introduction)
We've used matrices mod $5$ to encrypt a simple message. The set of possible 2 by 2 matrices mod $5$ that we can use as an encryption key is an important set in cryptography. It's called a general linear group and written $\text{GL}(2,\mathbb{Z}_5)$. We can generalize this to $m$ by $m$ matrices mod $n$ and write $\text{GL}(m,\mathbb{Z}_n)$, though generally we require that $n$ be a prime. With each of the problems below, a single sentence or two is enough to answer the question.
- If we want $A$ to serve as a valid matrix for encryption, what must we require about $A$? One sentence is fine.
- If $A\in \text{GL}(2,\mathbb{Z}_5)$, show that $A^{-1}\in \text{GL}(2,\mathbb{Z}_5)$.
- If $A\in \text{GL}(2,\mathbb{Z}_5)$ and $B\in \text{GL}(2,\mathbb{Z}_5)$, why is $AB\in \text{GL}(2,\mathbb{Z}_5)$?
- Prove that if we know for some integer $k$ that $A_1,A_2,A_3,\ldots,A_k \in \text{GL}(2,\mathbb{Z}_5)$, then we know $A_1A_2A_3\cdots A_k\in \text{GL}(2,\mathbb{Z}_5)$.
- Is $\text{GL}(2,\mathbb{Z}_5)$ a group? (Which of the group properties did we not show above? Are they true?)
- Do your arguments above hold when considering $\text{GL}(m,\mathbb{Z}_n)$ for every $m,n \in \mathbb{N}$ such that $n\geq 2$? A conjecture with a reasonable justification (not a complete a proof) is fine in this part.
In the definition of a group, it said that there exists an element $e\in G$ such that $ex=xe=e$ for each $x\in G$. It refers to this element as the identity. Could there be two such elements? Similarly, could an element have two inverses? The next problem has you show that the identity and inverses are unique.
Problem 41 (The Identity And Inverses Are Unique)
Suppose that $(G,\cdot)$ is a group.
- Prove that the identity of the group is unique.
- Prove that if $x\in G$, then the inverse of $x$ is unique.
You then need to show why $e_1=e_2$. Your second proof is similar.
Problem 42 (The GCD Theorem Proof)
Prove the GCD Theorem.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Hint: If you intersect $\text{span}(a,b)$ with the natural numbers, then you can apply the well ordering principle to get the smallest positive element $d$ of this intersection. You then just have to show that this smallest positive element $d$ is the greatest common divisor. This requires that you show
- that $d$ is a common divisor, and
- that $d$ is the greatest common divisor.
Showing that $d$ divides both $a$ and $b$ is the trickiest bit. First, we know that their span is closed. When we use the division algorithm to obtain $a=qd+r$, so in particular $r=a-qd$, show that $r$ is in the span of $a$ and $b$. Once you've done this, you should be able to explain why the remainder must be zero (how large is the remainder in relation to $d$, and what did you define $d$ as?).
We've spent quite a bit of time looking at modular multiplicative inverses and the sets $\mathbb{Z}_n$ and $U(n)$. Let's take a minute and explore an encryption problem that uses these sets.
Definition (Affine Encryption Key)
Suppose we have an alphabet with $n$ letters. Set up a 1-1 correspondence between the letters in your alphabet and the integers 0 to $n-1$. As an example, we could let $n=27$ for the standard alphabet with 26 letters and a space (the 27th letter which we'll number 0), and then use the correspondence in the table below.
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
Pick an integer $m\geq n$. Then an affine encryption key is an invertible function \( f:\mathbb{Z}_m \to \mathbb{Z}_m\) defined by $$f(x)=ax+b\pmod {m}$$ for some $a,b\in\mathbb{Z}_m$.
Problem 43 (Affine Encryption Key Introduction)
If we let $m=31$, then we can use the function $f(x)=5x+12\pmod m$ to encrypt the message "save them" by (1) swapping the letters to the numbers (19,1,22,5,0,20,8,5,13) and then (2) applying $f(x)$ to each letter to obtain the encrypted numbers (14, 17, 29, 6, 12, 19, 21, 6, 15).
- Find $c,d\in \mathbb{Z}_{31}$ so that the inverse of $f$ is $f^{-1}(x)=cx+d$ where $c,d\in \mathbb{Z}_{31}$.
- If instead we let $m=27$, then find the inverses of $f(x)=2x+17\pmod{27}$ or explain why it cannot be done.
- Give an example of nonzero $a,b\in \mathbb{Z}_{27}$ so that $f(x)=ax+b\pmod{27}$ is not invertible.
You've been studying groups since you started adding integers back in grade school. Just about every idea we've encountered since the start of the semester has also been a group. Now that we have isolated the key properties that make up a group, we need to become comfortable with showing that sets with a binary operation are groups, i.e. we need to become comfortable with checking the four properties of closure, associativity, identity, and inverses.
Let's practice showing that some sets are groups by showing that $\mathbb{Z}_n$ and $U(n)$ are groups. If we already showed a key fact in a previous problem, feel free to refer to problem by name and state the fact that was proved there. We have already shown most of the reasons why the sets below are groups.
Problem 44 ($\mathbb{Z}_n$ and $U(n)$ are groups)
Show the following. You need to briefly explain why the set together with its binary operation satisfies the definition of a group.
- For each $n\geq 1$, the set $\mathbb{Z}_n$ is a group under addition mod $n$.
- For each $n\geq 2$, prove that $U(n)$ is a group under multiplication mod $n$.
Try to solve the problems above without looking up the definition of a group.
If you need to, click here to show the definition of a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
Because of how we defined groups, anytime we span a collection of permutations of a set $X$ we should get a group. The next problem has you show this. Each question can be answered by referring to things we have already shown.
Problem 45 (Spans Of Permutations Are Subgroups)
Let $X=\{1,2,3,\ldots,n\}$. Let $S_n$ be the set of all permutations of $X$ (so we know there are $n!$ such permutations).
- Show that $S_n$ is a group under function composition $\circ$.
- If $H$ is a subset of $S_n$ that is closed (under composition combinations of permutations), prove that $H$ is a group under function composition.
- Let $S$ be a nonempty subset of $S_n$. Show that $\text{span}(S)$ is a group under function composition.
In the previous problem, we saw if $S\subseteq S_n$ then $\text{span}(S)$ is a not only just a subset of the group $S_n$, but is itself a group. The operation we use in the smaller group $(\text{span}(S),\circ)$ comes from the operation we used in the larger group $(S_n,\circ)$. Because of this close connection, we call $\text{span}(S)$ a subgroup of $S_n$ and write $\text{span}(S)\leq S_n$. Let's now make a formal definition.
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
Problem 46 (The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses)
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- If $a,b\in H$, then $ab\in H$. (We say $H$ is closed under the group operation.)
- If $a\in H$, then $a^{-1}\in H$. (We say $H$ is closed under taking inverses.)
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
The following problem again asks you to make sure you are comfortable with the definitions of a binary operation and a group.
Problem 47 (Can We Use Division To Create A Group)
Let $G=\mathbb{R}$ and $H=\mathbb{R}\setminus \{0\}$.
- Show that division $a\div b$ is not a binary operationon $G$.
Definition (Binary Operation)
Let $G$ be a set. A binary operation on $G$ is a way of combining two elements of $G$ to obtain a new element in $G$. Formally, we just say that a binary operation $*$ is function $*:G\times G\to G$, and we use the notation $a*b$ to represent the function notation $*(a,b)$.
- Show that division $a\div b$ is a binary operation on $H$.
- Since division is a binary operation on $H$, determine if $(H,\div)$ is a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- Does $e=1$ satisfy the property of being an identity?
- If $x\in H$, find an inverse $x^{-1}\in H$ or explain why none exists.
- Is the operation $\div$ associative?
Definition ($|a|$ and $|G|$ - Order For Elements and Groups)
Let $G$ be a group with identity $e$, and let $g\in G$.
- The $\textdef{order}$ of $G$, denoted $|G|$, is the cardinality of $G$.
- The $\textdef{order}$ of $g$, denoted $|g|$, is the smallest positive integer $n$ such that $g^n = e$, if such an $n$ exists. If no such $n$ exists, we say $g$ has infinite order.
Definition (The Euler Phi Function)
The Euler phi function $\varphi:\mathbb{Z}\to\mathbb{Z}$ is defined by letting $\varphi(n)$ equal the order of $U(n)$.
Problem 48 (Orders Of $\mathbb{Z}_n$ And $U(n)$ And Their Elements)
We've already shown that $\mathbb{Z}_n$ under addition mod $n$ and $U(n)$ under multiplication mod $n$ are groups.
- For each $n$ between 2 and 10, compute the order of $Z_n$ and the order of each element of $\mathbb{Z}_n$. Organize your work into a table where you first make a list of the elements, and then underneath each element state the order. For example, if $n=6$ then our table would look like the one below. $$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Element}&0&1&2&3&4&5\\\hline \text{Order}&1&6&3&2&3&6\\\hline \end{array}$$
- For each $n$ between 2 and 10, compute the order of $U(n)$ (state $\varphi(n)$) and then compute the order of each element of $U(n)$. You can check your work with the sage code below. I kept the numbers under 10 because you can do these by hand (or in your head) fairly quickly. Make sure you do enough by hand that you feel comfortable with this process.
- You should have noticed that $U(8)$ and $U(10)$ both have order 4. Is there a 1-1 correspondence between these two groups that matches elements with the same order?
Here's some Sage code you can use to check your computations with $U(n)$.
for n in (2..20):
Zn = Integers(n)
Un = [x for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
show(table(["U("+str(n)+r") has order $\varphi($"+str(n)+"$)=$"+str(len(Un))+
".The elements, with orders below them, are listed below."]))
orders=[x.multiplicative_order() for x in Un] #This computes the multiplicative order of each element.
show(table([Un,orders])) #This creates a table of elements (top row) and their orders (bottom row).
Click to see the definitions of a group and subgroup, as well as the subgroup test.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
Problem 46 (The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses)
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- If $a,b\in H$, then $ab\in H$. (We say $H$ is closed under the group operation.)
- If $a\in H$, then $a^{-1}\in H$. (We say $H$ is closed under taking inverses.)
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
Problem 49 (Cancellation Laws For Groups)
Suppose $G$ is a group. Let $a,b,c\in G$. Prove that if $ca=cb$, then $a=b$. A similar proof will show that if $ac=bc$, then $a=b$.
Problem 50 (The Inverse In A Finite Group Is A Power Of The Element)
Let $G$ be finite group with $a\in G$. Prove that there exists a positive integer $k$ such that $a^k=a^{-1}$.
Problem 51 (Inverses In Groups)
Suppose that $G$ is a group with $a,b\in G$.
- Prove that the inverse of $a^{-1}$ is $a$.
- Prove that the inverse of $ab$ is $b^{-1}a^{-1}$.
- If $a_1,a_2,a_3,\ldots, a_n\in G$, state the inverse of $a_1a_2a_3\cdots a_n$. Use induction to prove your claim.
Problem 52 (Heisenberg Matrix Group)
Let $G$ be the set of all 3 by 3 matrices with entries in the real numbers of the form $$\begin{bmatrix}1&a&b\\0&1&c\\0&0&1\end{bmatrix}.$$ Prove that $G$ is group under matrix multiplication. This group is often called the Heisenberg group and is connected to the Heisenberg uncertainty principle. See page 51 in your text for an interesting historical fact.
Problem 53 (Finite Subgroup Test)
Let $G$ be a group. Suppose that $H$ is a nonempty finite subset of $G$ and that $H$ is closed under the operation of $G$ (so if $a,b\in H$, then we must have $ab\in H$). Prove that $H$ is a subgroup of $G$.
Problem 54 (The Intersection Of Two Subgroups)
Suppose that $G$ is a group and that $H$ and $K$ are subgroups of $G$. Prove that $H\cap K$ is a subgroup of $G$.
Problem 55 (The Union Of Two Subgroups)
Suppose that $G$ is a group and that $H$ and $K$ are subgroups of $G$. Is $H\cup K$ a subgroup of $G$? Either prove that is, or find a counterexample.
Definition (Abelian Group)
Let $G$ be a group. If $ab=ba$ for every $a,b\in G$ (so the group operation is commutative), then we say that $G$ is Abelian.
Definition ($Z(G)$ - Center Of A Group)
Let $G$ be a group. The center of the group, written $Z(G)$, is the set of elements $x\in G$ that commute with every element of $G$, which we can write symbolically as $$Z(G)=\{x\in G\mid gx=xg \text{ for all } g\in G\}.$$
Problem 56 (The Center Of Group Is A Subgroup)
Prove that the center $Z(G)$ of a group $G$ is a subgroup of $G$. If $G$ is Abelian, then what is $Z(G)$?
Problem 57 (Powers Of Products In An Abelian Group)
Suppose $G$ is an Abelian group. Prove that if $a,b\in G$, then $(ab)^2=a^2b^2$. Then use induction to prove that if $a,b\in G$, then $(ab)^n=a^nb^n$ for each $n\in \mathbb{N}$.
Problem 9(Simple Shift Repetition)
Let's now devise a way to not only encrypt a message, but also keep track of who has seen the message? There are several ways to do this. Let's look at an example that involves repeated application of the same encrpytion key. For this example, let's use the encryption key $\phi_4:S\to S$ (the simple shift permutation that shifts right 4).
A group of military commanders decide to send messages using a message chain. The message passes sequentially from one person to the next, where at each stage they apply the encryption key to the ciphertext before sending it on. If I want to send the plain text message $attackatdawn$, then I'd send the message $exxegoexhear$ to the person after me in the chain. This person would decipher the text using $\phi_4^{-1}$ (shift left 4), and then apply $\phi_4$ to the cipher text $exxegoexhear$ and then send the ciphertext $ibbiksibliev$ to the person after them in the chain. This would repeat until the message made it to every commander.
- You receive the cipher text $skkzgzkomnz$. What is the plain text message? How many people have seen this message?
- How many commanders can we include in this encryption scheme and still tell who sent the message?
- If we use $\phi_5$ instead of $\phi_4$, how many commanders can we include in this encryption scheme and still tell who sent the message?
- Is there an encryption key $\phi_n$ so that $\phi_n^2=\phi_0$. In other words, is there an encryption key $\phi_n$ that will only allow up to two commands to be in the chain?
Definition (Subgroup Generated By An Element)
Let $G$ be a group and $a\in G$. Then the subgroup generated by $a$ is the set $$\langle a\rangle = \{a^n\mid n\in\mathbb{Z}\},$$ where we define $a^0=e$ and $a^{-n}=(a^{-1})^n$.
Problem 58 (The Subgroup Generated By An Element Is Actually A Subgroup)
Let $G$ be a group with $a\in G$. Show that $\langle a\rangle$, using the definition above, is a subgroup of $G$.
Problem 59 (The Intersection Of Two Subgroups Of $\mathbb{Z}$)
Let $G=\mathbb{Z}$. Because the group operation is addition, remember that $a^2$ actually means $a+a$, and $a^5=a+a+a+a+a=5a$. Beware of this issue, as $a^n$ actually means $na$ because the group operation is addition when working in $\mathbb{Z}$.
- What is $\langle 2\rangle$? What is $\langle 3\rangle$? Convince yourself that $\langle 2\rangle\cap \langle 3\rangle = \langle 6\rangle$.
- What is $\langle 4\rangle$? What is $\langle 6\rangle$? Find an integer $c$ so that $\langle c\rangle=\langle 4\rangle\cap \langle 6\rangle$? Prove that your result is true.
- If $a,b\in \mathbb{Z}$, then conjecture what $c$ should equal so that $\langle c\rangle=\langle a\rangle\cap \langle b\rangle$. You don't have to prove this result (unless you'd rather prove this result than proving part 2).
Definition (The Subgroup $n\mathbb{Z}$)
For each $n\in \mathbb{N}$ we define $n\mathbb{Z}$ to be the subgroup $\langle n\rangle = \{kn\mid k\in \mathbb{Z}\}$ of the group $\mathbb{Z}$ under addition. This is just the multiples of $n$.
When we were working with simple shift permutations of the standard 26 letter alphabet, we showed that the set of all simple shift permutations, denoted $H=\{\phi_n\mid n\in\mathbb{Z}\}$, is actually a set that consists of just 26 distinct elements, namely we showed that $H=\{\phi_0,\phi_1, \ldots,\phi_{25}\}$. We can generate each of these simple shifts using $\phi_1$, and the order of $\phi_1$ is $|\phi_1|=26$. Using the language of groups, we showed that $$H =\langle \phi_1\rangle = \{\phi_0,\phi_1, \ldots,\phi_{25}\}.$$ This is true because if $n\in \mathbb{Z}$, then we can use the division algorithm to write $n=26q+r$ where $0\leq r<26$. Then we know that $$\phi_1^{n}=\phi_1^{26q+r}=\phi_1^{26q}\circ \phi_1^r = \phi_0\circ \phi_r = \phi_r.$$ This shows that $\langle \phi_1\rangle\subseteq \{\phi_0,\phi_1, \ldots,\phi_{25}\}$, and the reverse set containment is obvious by definition of $\langle \phi_1\rangle$. In addition, we know that $\phi_i= \phi_j$ if and only if $i-j$ is a multiple of $26$, which means that the 26 elements given in the list $\phi_0,\phi_1, \ldots,\phi_{25}$ are distinct. The fact that $H=\{\phi_0,\phi_1, \ldots,\phi_{25}\}$ tells us that $H$ has at most 26 elements, and the fact that each of the elements in the list $\phi_0,\phi_1, \ldots,\phi_{25}$ are distinct tells us that $H$ has exactly 26 elements.
We now generalize the above work to show that if an element of a group has order $n$, then $\langle a\rangle$ must always consist of the elements $\{e,a,a^2,\ldots, a^{n-1}\}$.
Problem 60 (Properties Of $\langle a \rangle$ When $a$ Has Finite Order)
Let $G$ be a group with $a\in G$. Suppose that the order of $a$ is $|a|=n$. Prove the following:
- We have $\langle a\rangle = \{e,a,a^2,\ldots, a^{n-1}\}$. (You are showing two sets are equal.)
- We have $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
- The order of an element equals the order of the subgroup generated by that element, namely $|a|=|\langle a\rangle|$. (How can you combine 1 and 2 to get this.)
Exercise (If $a^k=e$, Then The Order Of $a$ Divides $k$)
Suppose that $a$ is a group element with order $n$. If $a^k=e$, prove that $k$ is a multiple of $n$.
Click to see a solution.
Suppose $a^k=e$. This means $a^k=a^0$, which from the previous problem is true if and only if $k-0$ is a multiple of $n$. This shows that $k=k-0$ is a multiple of $n$.
Exercise (Properties Of An Element With Infinite Order)
Let $G$ be a group with $a\in G$. Suppose that the order of $a$ is infinite. Show that $a^i=a^j$ if and only if $i=j$, and state the order of $\langle a\rangle$.
Click to see a solution.
Suppose the order of $a$ is infinite. Then by definition this means that $a^n\neq e$ unless $n=0$. Clearly if $i=j$ then $a^i=a^j$. We only need to prove the converse of this statement. Suppose that $a^i=a^j$, and assume without loss of generality that $i\geq j$. Then $a^{i-j}=e$ (just multiply both sides on the right by $a^{-j}$). Because $a$ has infinite order, then we know $a^k\neq e$ for any positive integer $k$. Since $i-j\geq 0$ and $a^{i-j}=e$, we must have $i-j=0$. This means $i=j$.
The next problem asks you to compute the center $Z(G)$ of a nonabelian group, and the result is not trivial group. The automorphisms of the square gave us a group with 8 elements. This group consisted of 4 rotations and 4 reflections. Similarly, for any regular $n$-gon we can construct the automorphism group which will have order $2n$ and consist of $n$ rotations and $n$ reflections.
Definition (The Dihedral Groups $D_{n}$)
For each integer $n\geq 2$, we define the dihedral group on $n$ vertices, written $D_{n}$, to be automorphism group of the regular $n$-gon. This group consists of $n$ rotations and $n$ reflections, so has order $2n$.
Problem 61 (The Center Of A Dihedral Group)
Let $G=D_4$, the automorphism group of the square. Recall that $Z(G)$ is the center of the group, or the set of elements that commute with every element of the group.
- What is $\langle R_{90} \rangle$? What is $\langle R_{180} \rangle$? What is $\langle R_{270} \rangle$? What is $\langle H \rangle$?
- Does $R_{90}\in Z(G)$? Explain. (Does $R_{90}$ commute with every element in $G$? In particular, does $R_{90}H=HR_{90}$?)
- Compute the center $Z(G)$ and show that it consists of more than just $R_0$. Make sure you can explain why each element is either in $Z(G)$, or not in $Z(G)$.
Every time you seen an Exercise in the problem set, you should spend a couple minutes trying to answer the question. These questions are designed as a quick check of some facts that you should be familiar with. Come up with a solution, and then click to see the solution.
Exercise (What Is The Group Operation On The Integers)
If we want to consider $\mathbb{Z}$ as group, then which operation do we use, addition or multiplication? Why? Which is a group, is it $(\mathbb{Z},+)$ or is it $(\mathbb{Z},\cdot)$?
Click to see a solution.
The integers are a group under addition (the sum of two integers is an integer, the identity is 0, the inverse of $n$ is $-n$, and addition is associative as an axiom). For multiplication, the inverse of $2$, which is $1/2$, is not an integer so $\mathbb{Z}$ is not closed under inverses. There is no multiplicative inverse of 0 as $0x\neq 1$ for any integer $x$.
Exercise (Are The Natural Numbers A Subgroup Of The Integers)
Is $\mathbb{N}$ closed under the operation of addition? Is $\mathbb{N}$ a subgroup of $\mathbb{Z}$?
Click to see a solution.
The sum of two positive integers is a positive integer, so $\mathbb{N}$ is closed under the operation of $\mathbb{Z}$ (which is addition). However, the inverse of $2$ under addition is $-2$, but $-2\notin \mathbb{N}$. This shows that $\mathbb{N}$ is not closed under taking inverses, and hence is not a group (so not a subgroup of $\mathbb{Z}$).
Take a moment to reread the problem The Span Of A Simple Shift. In this problem, we looked at the span of various simple shift permutations. We saw many patterns that we conjectured without proof. In particular, we noticed that two simple shifts $\phi_i$ and $\phi_j$ had the same span if they had the same greatest common divisor with 12 (the size of the alphabet). It's time to prove this conjecture, as well as many more.
The following problem requires that you use the GCD theorem. If you let $d=\gcd(n,k)$, then remember that there are integers $s$ and $t$ such that $d=sn+tk$. This will be your key tool in working with the greatest common divisor.
Problem 62 ($\langle a^k\rangle = \langle a^{\gcd(k,|a|)}\rangle$)
Let $a$ be an element of order $n$ and let $k\in\mathbb{N}$. Prove that $\langle a^k\rangle = \langle a^{\gcd(k,n)}\rangle$.
Problem 63 ($|a^k| = |a|/\gcd(k,|a|)$)
Let $a$ be an element of order $n$.
- If $d$ is a divisor of $n$, then prove that $|a^d|=n/d$.
- For any $k\in \mathbb{N}$, prove that $|a^k| = n/\gcd(k,n)$.
The previous two problems are the key tools to unlocking all of our other conjectures about simple shift permutations. In particular, the order of a simple shift permutation on $n$ letters will always be a divisor of $n$. Let's first make a new definition, a cyclic group, to generalize any group that behaves like the simple shift permutations.
Definition (Cyclic Group)
Let $G$ be a group. If there exists an element $a\in G$ such that $\langle a\rangle=G$, then we say that $G$ is a cyclic group.
Exercise (Cyclic Groups Are Abelian)
Suppose that $G$ is a cyclic group. Prove that $G$ is an Abelian group.
Click to see a solution.
Since $G$ is cyclic, we know that there exists some $a\in G$ with $\langle a\rangle = G$. Let $x,y\in G$. We need to show that $xy=yx$. But we know that $x=a^m$ and $y=a^n$ for some $n,m\in \mathbb{Z}$ because $G$ is cyclic. This means that $$xy=a^ma^n=a^{m+n}=a^{n+m}=a^na^m=yx,$$ which is what we needed to show.
We need to review the definition of the order of a group.
Definition ($|a|$ and $|G|$ - Order For Elements and Groups)
Let $G$ be a group with identity $e$, and let $g\in G$.
- The $\textdef{order}$ of $G$, denoted $|G|$, is the cardinality of $G$.
- The $\textdef{order}$ of $g$, denoted $|g|$, is the smallest positive integer $n$ such that $g^n = e$, if such an $n$ exists. If no such $n$ exists, we say $g$ has infinite order.
If you feel like you need extra practice with this definition, then please complete the following exercise.
Exercise (Order Is The Smallest Positive Integer)
Suppose we know that $a^6=e$.
- Explain why this is not enough information to state the order of $a$. (Look at the definition. What are we missing?)
- In addition to knowing that $a^6=e$, someone else notices that $a^4=e$. Prove that the order of $a$ cannot be 4. In particular show that $a^2=e$, so the order of $a$ is either $2$ or $1$.
Click to see a solution.
- The order of an element is the SMALLEST positive integers $n$ such that $a^n=e$. If all we know is that $a^6=e$, then the order might be 6, or some number less.
- If we know that both $a^6=e$ and $a^4=e$, then since $6=4+2$ (the division algorithm), we know that $e=a^6=a^{4+2}=a^4a^2=ea^2=a^2$. This shows that $e=a^2$, which means the order now can at most be 2.
We know that the following facts are true if $a$ is an element or order $n$.
- $\langle a\rangle = \{e,a,a^2,\ldots, a^{n-1}\}$.
- $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
- $|a|=|\langle a\rangle|$.
- $\langle a^k\rangle = \langle a^{\gcd(k,n)}\rangle$.
- If $d$ is a divisor of $n$, then $|a^d|=n/d$.
- For any $k\in \mathbb{N}$, we have $|a^k| = n/\gcd(k,n)$.
Use these facts to prove the next problem.
Problem 64 ($\langle a^i \rangle = \langle a^j \rangle$ iff $\gcd(i,n)=\gcd(j,n)$)
Let $G$ be a group. Suppose that $a\in G$ has order $n>1$. Prove the following two facts:
- If $G$ is a cyclic group, then the order of $a$ divides the order of the group.
- We have $\langle a^i \rangle = \langle a^j \rangle$ if and only if $\gcd(i,n)=\gcd(j,n)$.
Click for a hint.
- If $G$ is cyclic, then pick a generator, say $b$. This means $G=\langle b\rangle$. Why does this mean $a=b^k$ for some $k$? Use this to show that $b$ has finite order, say $m$. Then use problem 63 with $b^k$, where $|b|=m$, rather than $a^k$ and $|a|=n$.
- Problem 63 will get you one direction, and problems 62 will get you the other.
The second fact proves the following three corollaries by letting $i=1$.
- We have $\langle a \rangle = \langle a^j \rangle$ if and only if $\gcd(n,j)=1$.
- A simple shift permutation $\phi_j$ on $n$ letters generates all simple shift permutations on $n$ letters if and only if $\gcd(n,j)=1$.
- An integer $j\in \mathbb{Z}_n$ is a generator of $\mathbb{Z}_n$ if and only if $\gcd(n,j)=1$.
What does this have to do with the problem When Does An Integer Have A Modular Multiplicative Inverse? You should see a connection between this problem and elements of $U(n)$.
We've spent a lot of time working with cyclic groups and cyclic subgroups generated by a single element. The Well ordering principle and the GCD theorem have shown up quite a bit in our work. Let's now show that any time we start with a cyclic group, then every subgroup must also be cyclic. We've already seen this fact when we consider the problem Simple Shift Repetition where we used repeated shifting to send encrypted message to several generals.
Problem 65 (Subgroups Of Cyclic Groups Are Cyclic)
Suppose that $G$ is a cyclic group generated by $a$. Suppose that $H$ is a subgroup of $G$. Prove that there exists $k\in\mathbb{Z}$ such that $H = \left<a^k\right>$. In other words, prove that $H$ is itself a cyclic group.
Click to see a hint.
How can you get the smallest positive integer $k$ such that $a^k\in H$?
We've seen several times in class that when we compute $\text{span}(a,b)$ for integers $a$ and $b$, then their span equals $\text{span}(d)$ for a single integer $d$. In particular, we've also seen that this integer $c$ is precisely $d=\gcd(a,b)$. What if instead we wanted to look at the span of $k$ integers $\{a_1,a_2,a_3,\ldots, a_k\}$. Is there a single number $d$ that has the same span? The previous problem says that YES there must be a single number that achieves this. We call this the greatest common divisor of $a_1,a_2,a_3,\ldots, a_k$. The next exercise emphasizes this.
Exercise (The Subgroups Of $\mathbb{Z}$ are $n\mathbb{Z}$)
We know that $n\mathbb{Z}$ is a subgroup of $\mathbb{Z}$ for every integer $n$. Show that these are the only subgroups of $\mathbb{Z}$. In particular this means that the span of $k$ integers, which is a subgroup of $\mathbb{Z}$, must be equal to $d\mathbb{Z}$ for some $d\in \mathbb{Z}$.
Click to see a solution.
The integers are a cyclic group, so every subgroup is also cyclic. If we let $H$ be a subgroup of $\mathbb{Z}$, then we know there exists $d\in\mathbb{Z}$ such that $H=\left<d\right>$. This shows that $H$ equals the set of multiples of $d$, which means that $H=d\mathbb{Z}$.
Definition (Symmetric Group on $X$)
Let $X$ be any set. The $\textdef{symmetric group}$ on $X$, denoted $\sym(X)$, is the set of all permutations of $X$. We denote by $S_n$ the symmetric group on $X = \{1,2,\ldots, n\}$ and call it the symmetric group of degree $n$.
Exercise (The Symmetric Group of Degree $n$ Is A Group)
Show that $S_n$ is a group under function composition.
Click to see a solution.
We've already shown this in our work earlier in the semester. Given any two permutations of $X$, their composition is a permutation of $X$ so $S_n$ is closed. We also know that function composition is associative. The identity permutation $\text{id}_X$ definded by $\text{id}_X(x)=x$ is an element of $S_n$. The inverse of $\alpha \in S_n$ is the inverse function $\alpha^{-1}$, which is again a permutation and so in $S_n$. This shows that $S_n$ satisfies the definition of being a group.
We've already seen that we can write every permutation as a product of disjoint cycles. The next problem has you show that there are other ways to write a permutations as a product. In particular, we'll show that given a cycle of length $n$, called an $n$-cycle, we can write that cycle as a product of 2-cycles, called transpositions.
Problem 65B (optional) (Every Disjoint Cycle Can Be Written As A Product Of Transpositions)
Start by convincing yourself that $(1,2,3,4,5)=(1,5)(1,4)(1,3)(1,2)$. This shows how to write a 5-cycle as a product of transpositions (2-cycles).
- Find another way to write $(1,2,3,4,5)$ as a product of transpositions. This shows that there are multiple ways to write a cycle as a product of transpositions.
- Suppose $m,n\in \mathbb{N}$ with $m\geq n$. Also suppose that $\alpha = (a_1,a_2,a_3, \ldots, a_n)\in S_m$ is a disjoint cycle. Give a way to rewrite $\alpha$ as a product of 2-cycles.
Definition ($A_n$ - Alternating Group of Degree $n$)
Let $n\in\mathbb{N}$. Suppose that $\alpha\in S_n$.
- We say that $\alpha$ is a transposition if $\alpha$ is a cycle $(a,b)$ of length 2.
- We say that $\alpha$ is an even permutation if we can write $\alpha$ as the product of an even number of transpositions. Otherwise, we say that $\alpha$ is odd.
- The alternating group of degree $n$, written $A_n$, is the subset of $S_n$ of all even permutations.
Exercise (Even Permutations)
Show that each permutation below is an even permutation.
- $(1,2)(3,4)$
- $(1,2,3)$
- $(1,2)(3,4)(1,2,3)$
- $()$
- $(1,4,3,5)(2,3,1,4,7,6)$
Click to see a solution.
With each permutation, we just have two show that when we write the permutation as a product of transpositions, that the number of them is even.
- The permutation $(1,2)(3,4)$ is already written as a product of two transpositions, so it's an even permutation.
- We can write $(1,2,3)=(1,3)(1,2)$, which is two transpositions.
- Combining the two parts above, we can write $(1,2)(3,4)(1,2,3) = (1,2)(3,4)(1,3)(1,2)$. This is a product of 4 transpositions, so the permutation is in $A_n$.
- The identity is a product of zero transpositions, which is even. Alternately, we can write the identity as the product $(1,2)(1,2)$, which is two transpositions.
- We can write $(1,4,3,5)=(1,5)(1,3)(1,4)$ and also $(2,3,1,4,7,6)=(2,6)(2,7)(2,4)(2,1)(2,3)$. This means that $$(1,4,3,5)(2,3,1,4,7,6) = (1,5)(1,3)(1,4)(2,6)(2,7)(2,4)(2,1)(2,3), $$ which is the product of 8 transpositions.
We can show that each of the permutations above is the product of an even number of transpositions, and hence an even permutation. However, there are many other ways to write each one. Could it be that some permutations can be written as a product of an even number of transpositions, and then written a different way as an odd number of permutations? We'll leave this as an open question, and come back to it if interest and/or time permits. Regardless, we can still show that the alternating group $A_n$ of degree $n$ is a subgroup of the symmetric group $S_n$. We'll do this to make sure we have some more practice with proving that subsets are subgroups.
Problem 65C (optional) (The Alternating Group Is A Subgroup Of The Symmetric Group)
Let $n\in \mathbb{N}$. Prove that $A_n$ is a subgroup of $S_n$.
- Do this using the problem The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses.
- Do this using the problem Finite Subgroup Test.
The day after the exam, we'll spend in class looking at some of the things in this link.
Definition (Group Isomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{isomorphism}$ if $f$ is a bijection and $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$. We say that $G$ and $H$ are isomorphic groups, and write $G\approx H$ if there exists an isomorphism between them.
The group $H_{26}$ of simple shift permutations on the standard 26 letter alphabet is an encryption group we have learned to work with. The group operation is function composition where the composition $\phi_{k}\circ \phi_j$ is equal to $\phi_{j+k} = \phi_{j+k+26n}$ for any integer $n$. This set is very similar to the group $\mathbb{Z}_{26}$ where the operation is addition mod 26. It's so similar, that when we've drawn Cayley graphs in class, we tend to leave off the $\phi$ and just write the subscripts. Because of this similarity, they should be isomorphic groups.
Exercise (The set of simple shift permutations on 26 letters is isomorphic to $\mathbb{Z}_{26}$.)
Prove that the function $f:H_{26}\to \mathbb{Z}_{26}$ defined by $f(\phi_j)=j$ is a group isomorphism.
Click to see a solution.
We have to show two things. We must show that the function is a bijection, and that the function preserves the group operations.
- This function is a bijection because it has an inverse, namely $f^{-1}(k)=\phi_k$.
- We now have to show that the functin perserves the group operation. To show this we compute
$$f(\phi_j\circ \phi_k) = f(\phi_{j+k})= f(\phi_{(j+k)\pmod {26}}) = (j+k)\pmod {26} = (f(\phi_j)+f(\phi_k))\pmod {26}.$$ This shows that $f(\phi_j\circ \phi_k) = (f(\phi_j)+f(\phi_k))\pmod {26}$, which means the the function preserves the group operation.
Exercise (Every Finite Cyclic Group Of Order N Is Isomorphic To Zn)
Let $H_n$ be the set of simple shift permutations on a set of $n$ letters so $H_n=\{\phi_k\mid 0\leq k\leq n\}$.
- Start by drawing the Cayley graphs of $H_7$ and $\mathbb{Z}_7$, just to make sure that the graphs are similar.
- Show that $f:H_n\to \mathbb{Z_n}$ defined by $f(\phi_k)=k$ is a group isomorphism. Remember, this means you must show that $f$ is a bijection (what's the inverse) and that $f(\phi_j\circ \phi_k) = (f(\phi_k)+f(\phi_j))\pmod n$.
- Show that if $G$ is a cyclic group of order $n$ with generator $a$, then the function $f:\mathbb{Z}_n\to G$ defined by $f(k)=a^k$ is a group isomorphism.
Click to see a solution.
The Cayley graphs of both $\mathbb{Z}_7$ and $H_7$ are simple cycles of length 7. We could even draw them inline using $$1\to 2\to 3\to 4\to 5\to 6\to 7\to 1\quad \text{and} \quad \phi_1\to \phi_2\to \phi_3\to \phi_4\to \phi_5\to \phi_6\to \phi_7\to \phi_1,$$ however, we'd need an arrow from 7 back to 1, rather than writing 1 twice. We drew these graphs together in class.
We now consider the function $f:H_n\to \mathbb{Z}_n$ defined by $f(\phi_k)=k$. Note first that we know $H_n=\{\phi_0, \phi_1,\phi_2, \ldots, \phi_{n-1}\}$. This means that given $x\in H_n$, we know $x=\phi_k$ for some integer $k$ with $0\leq k< n$. This also means that $f(x)$ is well defined, as the output definitely lies in $\mathbb{Z}_n$. To show that $f$ is an isomorphism, we must show that $f$ is a bijection and that $f$ preserves the group structure. We first show that $f$ is a bijection. Let $g:\mathbb{Z}_n\to H_n$ be defined by $g(k)=\phi_k$ for each $k\in\mathbb{Z}_n$. We then compute $f(g(k))=f(\phi_k)=k$ for each $k\in\mathbb{Z}_n$. Given $x\in H_n$, we know $x=\phi_k$ for a unique $k\in \mathbb{Z}_n$. We then compute $g(f(x))=g(f(\phi_k))=g(k)=\phi_k=x$ for each $x\in H_k$. This shows that $g$ is the inverse of $f$ and so $f$ is a bijection. We now must show that $f$ preserves the group structure. Given $x,y\in H$, we find integers $j$ and $k$ so that $x=\phi_j$ and $y=\phi_k$. Note that we know $\phi_j\circ\phi_k=\phi_{j+k}$, and we also know that $\phi_m=\phi_{m\pmod n}$ for any integer $m$. We can then compute $$f(x\circ y)=f(\phi_j\circ\phi_k)=f(\phi_{j+k})=f(\phi_{(j+k)\pmod n}) = (j+k)\pmod n = f(x)+f(y).$$
We now generalize the above result to work for any cyclic group $G$. Let $G$ be a cyclic group of order $n$ with generator $a$. Consider the function $f:\mathbb{Z}_n\to G$ defined by $f(k)=a^k$. We must show that $f$ is an isomorphism. Note that we have already shown that $G=\langle a \rangle=\{a^0, a^1, \ldots, a^{n-1}\}$ and that the $n$ elements listed to the left are distinct. This means that given any $x\in G$, there is a unique nonnegative integer $k$ that is less than $n$ such that $x=a^k$. The inverse of $f$ is the function $g:G\to \mathbb{Z}_n$ defined by $g(x)=k$ where $k$ is the unique integer with $0\leq k<n$ such that $x=a^k$. You can check that $f(g(x))=x$ and $g(f(k))=k$ for each $x\in G$ and $k\in\mathbb{Z}$ which means that $f$ is bijective as $g$ is its inverse.
We now need to show that $f$ preserves the group structure. Let $j,k\in\mathbb{Z}$. If $j+k<n$, then we know $(j+k)\pmod n=j+k$. Otherwise, we know that $(j+k)\pmod n=j+k-n$. In either case, we know that there exists an integer $q$ so that $(j+k)\pmod n=j+k+qn$. We can now compute $$ f((j+k)\pmod n) =a^{(j+k)\pmod n} =a^{j+k+qn} =a^ja^ja^{qn} =a^ja^je =a^ja^j =f(j)f(k) .$$ This shows that $f$ preserves the group structure, and complete the proof that $f$ is an isomorphism.
The previous exercise shows that any time we have a cyclic group of order $n$, then we are basically working with a structure that's very similar to $\mathbb{Z}_n$. The names of the elements may be changed, but otherwise it's basically identical. The next problem has you show that a similar fact is true for infinite cyclic groups.
Problem 66 (Every Infinite Cyclic Group Is Isomorphic to $\mathbb{Z}$)
Suppose $G$ is a cyclic group of infinite order. Prove that $ \mathbb{Z}\cong G$. In other words, produce a function $f:\mathbb{Z}\to G$ and show that $f$ is an isomorphism.
Any time we use a single element $a$ of a group and construct the set $\left<a\right>$, we are creating a cyclic group. Earlier in the semester we called this the span of a single permutation. The next problem has you practice using this notation, as well as practice computing the order of an element in various groups.
Problem 67 (SKIP) (Practice With Cyclic Subgroups)
In each part below, you are given a group. Find an integer $n$ so that the given group $G$ is isomorphic to $\mathbb{Z}_n$. If you were to create an isomorphism $f:\mathbb{Z}_n\to G$, what value would you assign to $f(1)$? The first one already has an answer.
- Let $G=\langle R_{270} \rangle$ as a subgroup of $D_{4}$, the automorphisms of a square.
- We know that $R_{270}$ has order 4, so this subgroup is isomorphic to $\mathbb{Z}_4$. To obtain an isomorphism, we'd just let $f(1)=R_{270}$, as $R_{270}$ is a generator for $\langle R_{270} \rangle = \{R_{270},R_{180},R_{90},R_{0}\}$.
- Let $G=\langle R_{30} \rangle$ as a subgroup of $D_{24}$, the automorphisms of a regular 24-gon.
- Let $G=\left<\begin{bmatrix}2&1\\1&0\end{bmatrix}\right>$ in the general linear group $\text{GL}(2,\mathbb{Z}_3)$. [Hint: Just as all the previous problems, start computing powers of this matrix until you obtain the identity.]
- Let $G=\{(),(1,2,3), (1,3,2)\}$ as a subgroup of the set of all permutations of $X=\{1,2,3\}$.
- Let $G=U(7)$. [Hint: You'll need to start by finding a generator.]
- Let $G=U(17)$.
When two groups are isomorphic, they must have the same order because the function $f$ is a bijection. However, not only do two isomorphic groups need to have the same cardinality, but in addition the bijection creates a correspondence between elements of the same order. Each group must have the same number of elements of each order, and any isomorphism must map an element of order $k$ to an element of order $k$. The next problem has you prove this.
Problem 68 (The Orders Of Elements Match In Isomorphic Groups)
Suppose that $f:G\to H$ a group isomorphism. Suppose that $f(g)=h$. Prove that the order of $g$ and the order of $h$ are the same, in other words show that $|g|=|h|$. In particular, since the only elements of order 1 in each group are the identities $e_G\in G$ and $e_H\in H$, then we must have $f(e_G)=e_H$.
Click here to see a partial proof that's missing one piece.
Suppose that $f:G\to H$ is an isomorphism and that $e_G$ and $e_H$ are the identities in $G$ and $H$ respectively. We first show that $f(e_G)=e_H$. Note that $e_Ge_G=e_G$. Apply $f$ to both sides to obtain $f(e_G)f(e_G)=f(e_G)$. Since $f(e_G)=f(e_G)e_H$, we now have $f(e_G)f(e_G)=f(e_G)\cdot e_H.$ Cancelling $f(e_G)$ from the left of both sides gives $f(e_G)=e_H$ as desired.
We now prove that if $a$ has order $n$, then $f(a)$ must have order $n$ as well. Suppose $a\in G$ has order $n$. This means that $n$ is the smallest positive integer such that $a^n=e_G$, or that $aa \cdots a=e$ (repeated $n$ times). If we apply $f$ to both sides of this equation, then we see that $f(a)f(a)\cdots f(a)=f(e_G)$. This means that $f(a)^n=f(e_G)$. Since we know $f(e_G)=e_H$, then we have shown $f(a)^n=e_H$ is the identity. This means the order of $f(a)$ must equal $n$. $\square$
What's missing? Pay close attention to the definition of order.
Problem 69 (Cayley Tables And Isomorophisms On A Group Of Order 4)
In the problem Orders Of $\mathbb{Z}_n$ And $U(n)$ And Their Elements we computed the orders of $U(n)$ of $n$ from 2 to 10. The groups $U(5)$, $U(8)$, and $U(10)$ all have order 4 (they have four elements). For $U(5)$, we can construct a multiplication table (called a Cayley table) that represents the binary operation of the group. We create this table exactly as we created the times tables in grade school, where we put the product $ab$ in the row corresponding to $a$ and the column corresponding to $b$. The table for $U(5)$ is shown below. $$\begin{array}{c|cccc} \cdot \text{ mod } 5 & 1&2&3&4 \\ \hline\hline 1 & 1&2&3&4 \\ 2 & 2&4&1&3 \\ 3 & 3&1&4&2 \\ 4 & 4&3&2&1 \\ \end{array}$$
- Construct a multiplication table, i.e. Cayley table, for $U(8)$ and $U(10)$. Which of these groups is isomorphic to $U(5)$?
- Let $G = \{a,b,c,d\}$ and $H=\{r,s,t,u\}$ and define the operation $*$ on $G$ in the table on the left below, and the operation $\times$ on $H$ by the table on the right below. $$ \begin{array}{c|cccc} * & a&b&c&d \\ \hline\hline a & a&b&c&d \\ b & b&d&a&c \\ c & c&a&d&b \\ d & d&c&b&a \\ \end{array} \quad\quad\quad \begin{array}{c|cccc} \times & r&s&t&u \\ \hline\hline r & t&u&r&s \\ s & u&t&s&r \\ t & r&s&t&u \\ u & s&r&u&t \\ \end{array}.$$ For each group, which element is the identity element? Which group is isomorphic to $U(8)$?
- Let $K=\{1,-1,i,-i\}$, which is a subset of the complex numbers (recall that $i=\sqrt{-1}$ and $i^2=-1$). Construct a multiplication table for $K$, and show that $K$ is isomorphic to one of the groups above.
To show that two groups are isomorphic, we must show that there is a bijection between them that preserves the group structures. In linear algebra, we encounter maps that preserve the group structure, but are not necessarily bijections. We called such maps linear transformations in linear algebra. In a general group setting, we call these maps homomorphisms. Here's a formal definition.
Definition (Group Homomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{homomorphism}$ if $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$.
When we want to know if a matrix is invertible, or serves as a valid encryption key, we can discover this by computing the determinant. If the determinant of the matrix is non zero, has a multiplicative inverse, then we can invert this matrix. We shows this was true as well even when working with matrix encryption mod $n$.
Problem 70 (The Determinant Map Is A Homomorphism)
Let $n$ be an integer greater than 1, and consider the general linear group $\text{GL}(2,\mathbb{Z}_n)$ of two by two invertible matrices mod $n$. Let $f$ be the determinant map $f:\text{GL}(2,\mathbb{Z}_n)\to U(n)$ defined by $f(A)=\det A$, i.e. defined by $$f\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)= (ad-bc)\pmod n.$$ Show that $f$ is a homomorphism. Prove this result by direct computation, rather than by claiming it was already shown to be true in a previous course.
The set of matrices that have determinant one is a special group of matrices. We can use this group of matrices to learn quite a bit about all matrices. Here's a formal definition.
Definition (Special Linear Group $\text{SL}(m,\mathbb{Z}_n)$)
We have already defined the general linear group $\text{GL}(m,\mathbb{Z}_n)$ to be the set of $m$ by $m$ invertible matrices with coefficients in $\mathbb{Z}_n$, together with the binary operation of matrix multiplication mod $n$. The set of matrices in $\text{GL}(m,\mathbb{Z}_n)$ that have determinant 1 is called the special linear group, and we write $$\text{SL}(m,\mathbb{Z}_n)=\left\{ a\in \text{GL}(m,\mathbb{Z}_n) \mid \det(a)=1 \right\}.$$
Problem 71 (The Special Linear Group Is A Subgroup Of The General Linear Group)
Prove that $\text{SL}(m,\mathbb{Z}_n)$ is a subgroup of $\text{GL}(m,\mathbb{Z}_n)$. Why is the set of matrices whose determinant equals 2 not a subgroup of the general linear group?
Let's start with two small groups $G$ and $H$, and from them create a larger group by using the Cartesian product $G\times H = \{(g,h)\mid g\in G, h\in H\}$. To turn this into a group, we'll just use the group operation independently on each component. What we need to do today is to show this actually gives a group, learn how to graph such a group, and then analyze how we find the order of an element $(g,h)$ in the product $G\times H$ if we know the orders of $g$ and $H$ in their respective groups. First, let's get a formal definition. Feel free to read along in chapter 8 of your text.
Definition (External Direct Products $G\times H$ or $G\oplus H$)
Suppose that $G$ and $H$ are both groups. The cartesian product $G\times H$ is the set $$G\times H = \{(g,h)\mid g\in G, h\in H\}.$$ The external product of $G$ and $H$ is this Cartesian product $G\times H$ together with the group operation $(g_1,h_1)\cdot(g_2,h_2)=(g_1g_2,h_1h_2)$. We'll use the notation $G\times H$ of $G\oplus H$ to talk about the external direct product of $G$ and $H$. We can also define the external direct product of $n$ groups. The definition is analagous, where instead of having two components, we now have $n$ components, and we multiply two elements of the external direct product by performing the product componentwise.
The first thing you should do is convince yourself that the external direct product is actually a group. This is a straightforward exercise that you should make sure you can do.
Exercise (The External Direct Product $G\oplus H$ is a Group of order $|G||H|$)
Prove that the external direct product $G\oplus H$ or $G\times H$ is a group. If both groups are finite, then show that the order of the external direct product is $|G||H|$.
Click to see a solution.
Let $G$ and $H$ be groups. The binary operation $(g,h)\times(a,b) = (ga,hb)$ is associative as we can compute $$((g,h)(a,b))(m,n)=(ga,hb)(m,n) = ((ga)m,(hb)n)$$ and similarly $$(g,h)((a,b)(m,n))=(g,h)(am,bn) = (g(am),h(bn)).$$ These two quantities are equal because the operation in both $G$ and $H$ is associative. The identity in $G\times H$ is simply $(e_g,e_H)$, and the inverse of $(g,h)$ is $(g^{-1},h^{-1})$. I'll let you show that these satisfy the requirements to be the identity and inverse.
If $G$ has order $|G|$ and $H$ has order $|H|$, and both are finite, then there are clearly $|G|$ choices for the first component, and $|H|$ choices for the second component. Hence the total number of elements in $G\times H$ is precisely $|G\times H|=|G||H|$.
Given a subgroup of $G$ and a subgroup of $H$, we can quickly create a subgroup of $G\times H$. This is what the next problem asks you to show. If you'd like a fun challenge, then prove that the converse of the following problem is true, or produce a counter example. Namely, if $C$ is a subgroup of $G\times H$, must it be true that $C=A\times B$ for some $A\leq G$ and $B\leq H$. First complete all the problems on this list, and then tackle this challenge.
Problem 72 (An External Direct Product Of Subgroups Is A Subgroup Of An External Direct Product)
Show that if $A$ is a subgroup of $G$ and $B$ is a subgroup of $H$, then $A\times B$ is subgroup of $G\times H$.
The next exercise has you compute the orders of a few elements in some external direct products, as it prepares you to tackle the problem after.
Exercise (Practice With Orders In External Direct Products)
In each part below, you are given an element $(g,h)$ and a group $G\oplus H$. Compute the order of $g$ in $G$, the order of $h$ in $H$, and the order of $(g,h)\in G\oplus H$.
- $(1,2)\in \mathbb{Z}_2\times\mathbb{Z}_3$
- $(1,2)\in \mathbb{Z}_6\times\mathbb{Z}_4$
- $(1,2)\in \mathbb{Z}_6\times\mathbb{Z}_8$
- $(10,20)\in \mathbb{Z}_{4000}\times\mathbb{Z}_{600}$
Click to see a solution.
- We know $|1| = 2$ and $|2|=3$, and we can compute $(1,2)^k$ for each $k$ from $1$ to $6$ to obtain the sequence $((1,2),(0,1),(1,0),(0,2),(1,1),(0,0))$. This shows that $|(1,2)|=6$.
- We know $|1| = 6$ and $|2|=2$, and we can compute $(1,2)^k$ for each $k$ from $1$ to $6$ to obtain the sequence $((1,2),(2,0),(3,2),(4,0),(5,2),(0,0))$. This shows that $|(1,2)|=6$.
- We know $|1| = 6$ and $|2|=4$. Computing $(1,2)^k$ for each $k$ from $1$ to $12$ will show that the order is 12. Alternately, notice that in the product $(1,2)^k$, the first component will only equal 0 when $k$ is multiple of 6. Similarly, the second component will only be 0 when $k$ is a multiple of $4$. The number 12 is the smallest number for which both components will equal 0.
- We know $|10| = 400$ and $|20|=30$. In the product $(10,20)^k$, the first component will only equal 0 when $k$ is multiple of 400, and the second component will only be 0 when $k$ is a multiple of $30$. The least common multiple of 400 and 30 is 1200, which is the order of $(10, 20)$
Did you see in the exercise that the order of $(g,h)$ is the least common multiple of $|g|$ and $|h|$? The next problem has you prove this fact in general.
Problem 73 (The Order Of An Element In An External Direct Product Is The Least Common Multiple Of The Orders Of The Elements)
If $g\in G$ has order $n$ and $h\in H$ has order $m$, prove that the order of $(g,h)$ in $G\times H$ is the least common multiple of $n$ and $m$.
Given $m,n\geq 2$, how many elements are in $GL(2,\mathbb{Z}_n)$? In other words, how many different matrix encryption keys are there, given the size of the matrix and what coefficients we'll allow. This is a nontrivial problem, but its answer provides a key to knowing how to decrypt a message by brute force. We'll find that knowing something about the special linear groups will help us answer this question. First, let's make an observation that should simplify some computations if we assume that $n$ is prime.
Exercise (The Order Of $U(p)$ When $p$ Is Prime)
If $p$ is a prime, then what is the order of $U(p)$? In other words, what is the Euler $\varphi$ function at $p$, namely what is $\varphi(p)$.
Click to see a solution.
If $p$ is prime, then every positive integer less than $p$ is relatively prime to $p$. This means that $U(p)=\{1,2,3,4,\ldots, p-1\}$, which means $|U(p)|=p-1$. The Euler $\varphi$ function is just the number of elements in $U(n)$, so we have $\varphi(p)=p-1$ for primes $p$.
If $n$ is not prime, then the set $U(n)$ does not contain every positive integer less than $n$, which makes it harder to work with $U(n)$ when $n$ is not prime.
Problem 74 (Conjecturing The Order Of General Linear Groups)
Let's focus on 2 by 2 matrices with entries in $\mathbb{Z}_p$ where $p$ is a prime. So we let $p$ be a prime and consider $G = \text{GL}(2,\mathbb{Z}_p)$.
- Here is a list of all 81 of the 2 by 2 matrices with entries in $\mathbb{Z}_3$. Underneath that list you'll see the determinant of each matrix has already been computed for you. How many matrices have determinant 1, in other words how many matrices are in $\text{SL}(2,\mathbb{Z}_3)$. How many matrices are invertible, i.e. how many matrices are in $\text{GL}(2,\mathbb{Z}_3)$? What patterns did you use to help you count?
n=3 matrices=[]; for i in [0..n-1]: for j in [0..n-1]: tempmatrices=[] for k in [0..n-1]: for l in [0..n-1]: tempmatrices.append(matrix(2,2,[i,j,k,l])) matrices.append(tempmatrices) show(table(matrices)) dets=[]; for i in [0..n-1]: for j in [0..n-1]: tempdets=[] for k in [0..n-1]: for l in [0..n-1]: tempdets.append(matrix(2,2,[i,j,k,l]).det().mod(n)) dets.append(tempdets) show(table(dets))
- This sage code below repeats the above with $n=5$. Use this to count how many matrices have determinant 1 (are in $\text{SL}(2,\mathbb{Z}_5)$) and then how many are invertible (are in $\text{GL}(2,\mathbb{Z}_5)$). What patterns did you use to help you count?
n=5 #Change this number as needed. matrices=[]; for i in [0..n-1]: for j in [0..n-1]: tempmatrices=[] for k in [0..n-1]: for l in [0..n-1]: tempmatrices.append(matrix(2,2,[i,j,k,l])) matrices.append(tempmatrices) #show(table(matrices)) #Uncomment this line (remove the #) if you want to see all the matrices. dets=[]; for i in [0..n-1]: for j in [0..n-1]: tempdets=[] for k in [0..n-1]: for l in [0..n-1]: tempdets.append(matrix(2,2,[i,j,k,l]).det().mod(n)) dets.append(tempdets) show(table(dets))
- You can modify the sage code above to let $n=7, 11, 13,$ etc. How many matrices are in $\text{SL}(2,\mathbb{Z}_7)$ and $\text{GL}(2,\mathbb{Z}_7)$? What patterns did you use to help you count?
- If $p$ is a prime, make a conjecture about the order of $\text{SL}(2,\mathbb{Z}_p)$ and the order of $\text{GL}(2,\mathbb{Z}_p)$. You do not have to prove your conjecture.
You should have noticed in the problem Conjecturing The Order Of General Linear Groups that the number of matrices with determinant 1 always equals the number of matrices with a fixed determinant $k$. What we would like to do next is find a nice way to prove this. To do so, we first need to talk about the product of a set and an element. This will allow us to take any matrix $a$ and multiply it by each matrix with determinant 1 to obtain all matrices whose determinants match $a$. Here's the formal definition of the product of a set and an element.
Definition (The Product Of A Set And An Element)
Let $H$ be a subset of a group $G$ and let $a\in G$. Then we define the product $Ha$ and $aH$ to be the sets $$Ha = \{ha \mid h\in H\}\quad \text{and}\quad aH=\{ah\mid h\in H\}.$$ If the group $G$ is Abelian, then we generally use the operation $+$ instead of $\cdot$, and so we'll write $H+a$ instead of $Ha$ and we'll write $a+H$ instead of $aH$. However, since the operation is commutative, we know that $a+h=h+a$, and so we have $$H+a = \{h+a \mid h\in H\} = \{a+h\mid h\in H\}=a+H.$$
Problem 75 (The Set Product $Ha$ Preserves Determinants)
Let $m=2$ and let $p$ be a prime (it could be any integer, but $U(p)$ is easier to understand when $p$ is prime). Let $H=\text{SL}(2,\mathbb{Z}_p)$ and $G=\text{GL}(2,\mathbb{Z}_p)$. Let $a\in G$, so $a$ is a 2 by 2 invertible matrix. Recall that the set $Ha$ is the set $$Ha=\{ha\mid h\in H\},$$ so to obtain an element in $Ha$, we just take a matrix $h$ with determinant 1 and then multiply it on the right by the matrix $a$.
- Let $b\in GL(2,\mathbb{Z}_p)$. Prove that $b\in Ha$ if and only if $\det(b)=\det(a)$.
- When you prove if $b\in Ha$ then $\det(b)=\det(a)$, you'll show that every matrix in $Ha$ has the same determinant as $a$.
- When you prove if $\det(b)=\det(a)$ then $b\in Ha$, you'll show that every matrix with the same determinant as $a$ must be in $Ha.$
- Prove that the function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection. (What is the inverse of multiplying on the right by $a$?)
- Explain why $|H|=|Ha|$, in other words the number of matrices whose determinant equals 1 is the same as the number of matrices whose determinant equals $\det(a)$.
Now that we've got a little practice with homomorphisms, we need to prove some general facts about them. In particular, it would be nice to know how homomorphisms interact with the identity, and how they interact with inverse. For the determinant map, we know that the determinant of the identity is 1, which means that the determinant of the identity matrix is the identity in $U(p)$. The homomorphism mapped the identity to the identity. In addition, if the determinant of a matrix $A$ is $k$, then the determinant of the inverse of $A$ is $k^{-1}$. This shows that the determinant of an inverse is the inverse of the determinant. The next problem has you show that these two facts are true for any homomorphism.
Problem 76 (Homomorphisms Preserve The Identity And Inverses)
Suppose that $f:G\to H$ is a homomorphism, and that $e_G$ and $e_H$ are the identities of $G$ and $H$ respectively.
- Prove that $f(e_G)=e_H$.
- In addition show that $f(a^{-1})=(f(a))^{-1}$.
Click to see a hint.
You know that $e_Ge_G=e_G$. How does $f(e_Ge_G)=f(e_G)$ help you know that $f(e_G)=e_H$? Remember to use the fact that $f$ is a homomorphism.
To show that $f$ preserves inverses, think about how you can prove that the determinant of an inverse is the inverse of the determinant. If we have two matrices $A$ and $B$ then we know that $|AB|=|A||B|$. If we know that $B=A^{-1}$, then we have $AA^{-1}=I$ and so we have $|A||A^{-1}|=|I|=1$. Since we know that $|A||A^{-1}|=1$, we can just multiply both sides on the left by $|A|^{--1}$ to get $|A^{-1}|=|A|^{-1}$. If you mimic this process with an arbitrary homomorphism, you should find the solution for any homomorphism. Just replace $|A|$ with $f(a)$. What you did in linear algebra is the key to the more generalized notion of a homomorphism.
Recall the determinant map. The special linear group was the set of things that got mapped to the identity in $U(p)$. In Linear algebra, you looked at linear transformations and defined the kernel of the linear transformation to be the set of vectors that mapped to zero. This is precisely the set of vectors that mapped to the additive identity. The set of vectors which map to the identity is a special set, that we now define to be the kernel of a homomorphism. The kernel is the center, or core, of a seed, and we'll soon see that understanding the kernel of a homomorphism is central, or core, to understanding most problems in mathematics. Please ask me in class to discuss applications of this idea that you have seen in other courses. You've been studying the kernel of a homomorphism for quite a while, without every putting a name to it.
Definition (Kernel Of A Homomorphism)
The kernel of a homomorphism $f:G\to H$ is the set of elements in $G$ that are mapped to the identity $e_H\in H$. In symbols, we'll write the kernel of $f$ as $$\ker(f)=f^{-1}(e_H) = \{g\in G\mid f(g)=e_H\}.$$
For any prime $p$, if we let let $G=GL(2,\mathbb{Z}_p)$ and we consider the homomorphism $f:G\to U(p)$ which is the determinant map, then we've already shown that the kernel of the determinant map, namely $f^{-1}(1)$, is the special linear group $SL(2,\mathbb{Z}_p)$. The kernel of the map was a subgroup of $G$. The next problem has you show this result in general, namely that the kernel of any homomorphism $f:G\to H$ is always a subgroup of $G$. Your proof should be almost identical to what you did for the special linear group.
Problem 77 (The Kernel Of A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism and that $e_H$ is the identity in $H$. Prove that the kernel of $f$, namely $\ker f$ or $f^{-1}(e_H)$, is a subgroup of $G$.
For the rest of today, we'll be looking at the set products $aH$ and $Ha$ and what they physical mean in Cayley graphs. Once we can see these sets in Cayley graphs, we'll have a very visual way to describe the remainder of the ideas in this course. The sets $aH$ and $Ha$ are so crucial to the rest of this course that they have been given a name and are referred to as cosets. Here is a formal definition
Definition (Cosets $Ha$ and $aH$)
Let $G$ be a group and let $H$ be a subgroup of $G$. Let $a\in G$. We say that the set product $aH$ is a left coset of $H$ and the set product $Ha$ is a right coset of $H$. Remember that when the group is Abelian and we use the symbol $+$ to represent the group operation, then we write $a+H$ for the left cosets and $H+a$ for the right cosets.
We have already seen cosets when working with matrices that have the same determinant. We've also seen cosets already when working with modular arithmetic. This next exercise has you practice this.
Exercise (Practice With Cosets Of $3\mathbb{Z}$)
Let $G=\mathbb{Z}$ and let $H=3\mathbb{Z}$, the multiples of $3$.
- List the elements of $0+H$, $1+H$, $2+H$, $3+H$, $4+H$, $5+H$, $17+H$, and $-11+H$.
- How many different sets did you get?
Click to see a solution.
We know that $H=\{\ldots,-6, -3, 0, 3, 6, \ldots\}$. Adding 1 to each entry gives $H=\{\ldots,-5, -2, 1, 4, 7, \ldots\}$, which is the same as the set of integers whose remainder is 1 after dividing by 3. Similarly we have $$\begin{align} 0+H &= \{\ldots,-6, -3, 0, 3, 6, \ldots\}, \\ 1+H &= \{\ldots,-5, -2, 1, 4, 7, \ldots\}, \\ 2+H &= \{\ldots,-4, -1, 2, 5, 8, \ldots\}, \\ 3+H &= \{\ldots,-3, 0, 3, 6, 9, \ldots\} = \{\ldots,-6, -3, 0, 3, 6, \ldots\} = 0+H,\\ 4+H &= \{\ldots,-2, 1, 4, 7, 10, \ldots\} = \{\ldots,-5, -2, 1, 4, 7, \ldots\} = 1+H,\text{ and}\\ 5+H &= \{\ldots,-1, 2, 5, 8, 11, \ldots\} = \{\ldots,-4, -1, 2, 5, 8, \ldots\} = 2+H. \end{align}$$ In our computations above, we see that $k+H$ is equivalent to $k\pmod 3+H$. Since $17\pmod 3=2$ and $-11\pmod 3=1$, we have that $17+H = 2+H$ and we also have $-11+H = 1+H$.
There are only three different cosets. The cosets are $0+H$, $1+H$, and $2+H$. Every other coset is equal to one of these.
Definition (Identification Graph Using Cosets)
Let $G$ be a group, and let $\mathcal{G}=(G,S)$ be the Cayley graph of $G$ using the elements in $S$ to construct the colored arrows. Let $H$ be a subgroup of $G$. The identification graph of $G$ using the right cosets of $H$ is a colored directed graph such that
- The set of vertices is the set of right cosets $\{Ha\mid a\in G\}$, and
- We draw a colored arrow from the coset $Ha$ to the coset $Hb$ if and only if there exists a colored arrow $(c,d)$ with $c\in Ha$ and $d\in Hb$ in the original Cayley graph.
If instead of using right cosets, we used left cosets $aH$ as the vertices, then we'd call the graph the identification graph of $G$ using the left cosets of $H$.
The identification graphs just described will generally be a smaller graphs than the original graph. Sometimes those graphs will themselves be Cayley graphs, and sometimes they won't. One of our goals right now is to determine under which conditions we'll obtain a Cayley graph after computing an identification graph.
Problem 78 (Exercise - Solution provided) (Practice With Identification Graphs On An Abelian Group)
Let $G = U(15)$. Consider the subgroups $A=\left<4\right> = \{1,4\}$ and $B= \left<14\right> = \{1,14\}$. We'll use the set $S=\{7,11\}$ to draw the Cayley graph of $G$.
- Start by drawing the Cayley graph of $G$ with generators in $S$. You can check your answer with the Sage code at the end of this problem.
- For each $g\in G$, compute the right cosets $Ag$ of $A$. Draw the identification graph of $G$ using right cosets of $A$. You should get a graph with 4 vertices (each vertex should have two numbers in it). The graph should look like the Cayley graph of $U(8)$ using the generating set $S=\{3,5\}$, shown in the sage code below.
- For each $g\in G$, compute the left cosets $gA$ of $A$. Draw the identification graph of $G$ using left cosets of $A$.
- For each $g\in G$, compute the right cosets $Bg$ of $B$. Draw the identification graph of $G$ using right cosets of $B$. Again you should get a graph with 4 vertices, however your graph should not be the same as that in part 2. You should obtain something similar to the graph of $U(10)$ using the generating set $S=\{3,9\}$, shown in the sage code below. Click "Evaluate" a few times as the way the computer displays this graph can change.
- For each $g\in G$, compute the left cosets $gB$ of $B$. Draw the identification graph of $G$ using left cosets of $B$.
- Why are the answer to 2 and 3 the same? Why are the answers to 4 and 5 the same?
n=15
S=[7,11]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
n=8
S=[3,5]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
n=10
S=[3,9]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
Problem 79 (Exercise - Solution Provided) (Practice With Identification Graphs On A Non Abelian Group)
Let $G$ be the automorphisms of the square, i.e. the dihedral group of order 8. Consider the subgroups $A=\left<R_{180}\right> = \{R_0,R_{180}\}$ and $B= \left<H\right> = \{R_0,H\}$. We'll use the set $S=\{R_{90}, V\}$ to draw the Cayley graph of $G$.
- Start by drawing the Cayley graph of $G$ with generators in $S$. You can check your answer with the Sage code at the end of this problem.
- For each $g\in G$, compute the right cosets $Ag$ of $A$. Draw the identification graph of $G$ using right cosets of $A$.
- For each $g\in G$, compute the left cosets $gA$ of $A$. Draw the identification graph of $G$ using left cosets of $A$.
- For each $g\in G$, compute the right cosets $Bg$ of $B$. Draw the identification graph of $G$ using right cosets of $B$.
- For each $g\in G$, compute the left cosets $gB$ of $B$. Draw the identification graph of $G$ using left cosets of $B$.
- Make a conjecture about what happens with identification graphs when $gA=Ag$.
R90="(1,2,3,4)" V="(1,4)(2,3)" S=[R90,V] G=PermutationGroup(S) G.cayley_graph().show(color_by_label=True)
Problem 80 (When Does $H=Ha$)
Let $H$ be a nonempty subset of a group $G$. Prove that $H$ is a subgroup of $G$ if and only if $Ha=H$ for every $a\in H$.
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Let's now turn our attention back to homomorphisms. We'll see very soon that there is a big connection between homomorphisms and cosets. For today, let's just focus on some more properties of homomorphisms, namely that homomorphisms preserve subgroups. If you've forgotten the definition of the image of a set under a function, then here is a reminder.
Definition (Definition.The image of a function $f(A)$)
Let $f:G\to H$ be a function and let $A$ be subset of $G$. Recall that the image of $A$ under $f$ is the set $$f(A)=\{f(a)\mid a\in A\}.$$
If the set $A$ is a subgroup, then we would expect that a homomorphism maps the subgroup $A$ to a subgroup of $H$. This is precisely what the next problem asks you to show.
Problem 81 (The Image Of A Subgroup Under A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism. Let $A$ be a subgroup of $G$. Show that $f(A)$ is a subgroup of $H$.
We now generalize some facts that we learned about the determinant map. We have already shown that the determinant map breaks up the set of possible matrices into equally sized cosets, where each coset consists of matrices of the same determinant. The next problem has you show that this property was not dependent on the determinant map, rather it has to do with the fact that the special linear group is a subgroup, and nothing more. You should find that your work on the problem The Set Product $Ha$ Preserves Determinants can almost be copied directly over to solve the next problem.
Problem 82 (Properties Of Cosets)
Let $G$ be a group, and let $H$ be a subgroup of $G$. Let $a,b \in G$. Prove the following:
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
We've seen that when we create an identification graph of $G$ using right cosets of $H$, we sometimes get a Cayley graph, and we sometimes don't. Today, we'll be focusing on the question, "When is an identification graph of $G$ using cosets of $H$ another Cayley graph?" To answer this question, we'll need to explore the properties of cosets in depth.
When working with the determinant map $f:GL(2,\mathbb{Z}_p)\to U(p)$, we have already shown that the kernel of this map is the special linear group $K=SL(2,\mathbb{Z}_p)$. We've also shown that the coset $Ka$ equals the set of all matrices whose determinant matches the determinant of $a$. Another way to say this is that $Ka$ equals the set of values $b\in G(2,\mathbb{Z}_p)$ such that $f(b)=f(a)$. A similar argument would show that $aK$ is the exact same set, which means we have $Ka=aK$. The next problem has you show that for any homomorphism $f:G\to H$ with kernel $K$, we always have $Ka=aK$ and that $Ka$ equals the set of $b\in G$ such that $f(b)=f(a)$.
Problem 83 (The Right And Left Cosets Of The Kernel Are Equal)
Suppose that $f:G\to H$ is a homomorphism. Let $K$ be the kernel of $f$ and let $a\in G$. Prove the following:
- The right coset $Ka$ equals the set of values $b\in G$ such that $f(b)=f(a)$, or symbolically we have $$Ka = \{b\in G\mid f(b)=f(a)\} = f^{-1}(f(a)).$$
- The left coset $aK$ equals the same set $\{b\in G\mid f(b)=f(a)\}$, which means the left and right cosets are the same or $Ka=aK$.
In the previous problem, we saw that any time $K$ is the kernel of a homomorphism, we can talk about left or right cosets and obtain the exact same result, namely $Ka=aK$ for every $a\in G$. Any time a subgroup of $G$ satisfies this result, we'd like to have a special name for that subgroup. We call these subgroups normal.
Definition (Normal Subgroup $N\trianglelefteq G$)
We say that a subgroup $N$ of $G$ is a normal subgroup of $G$ if for each $a\in G$ the right coset $Na$ and left coset $aN$ are equal, so we have $Na=aN$ for every $a\in G$. We write $N\trianglelefteq G$ to mean that $N$ is a normal subgroup of $G$.
Before we can move too much farther, we need to prove some additional properties about cosets. We have already shown the following for a subgroup $H$ of the group $G$ with $a,b\in G$:
- We know $a\in Ha$.
- We know $Ha=H$ if and only if $a\in H$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
Let's add to this list of properties.
Problem 84 (Properties Of Cosets Part Two)
Let $H$ be a subgroup of $G$. Let $a,b\in G$. Prove the following facts about cosets.
- We have $Ha=Hb$ if and only if $ab^{-1}\in H$.
- We must have $Ha=Hb$ or $Ha\cap Hb=\emptyset$.
- We have $Ha=aH$ if and only if $aHa^{-1}=H$.
We've already seen all of these properties before when studying modular arithmetic. Let $G=\mathbb{Z}$ and let $H=n\mathbb{Z}$ for some $n\in\mathbb{N}$. The cosets of $H$ are $r+n\mathbb{Z}$ for $0\leq r<n$.
- The first property above states that $a+n\mathbb{Z}=b+n\mathbb{Z}$ if and only if $a-b\in n\mathbb{Z}$. Wait, this just says two numbers have the same remainder if and only if their difference is a multiple of $n$.
- The second property above states that either $a$ and $b$ have the same remainder, or they don't. It basically states that remainders are unique.
- The third property is trivial for $\mathbb{Z}$ because $\mathbb{Z}$ is an Abelian group and we always know $a+n\mathbb{Z}=n\mathbb{Z}+a$.
Problem 85 (The Set Product Is A Binary Operation On Cosets Of Normal Subgroups)
Suppose that $N$ is a normal subgroup of $G$. Let $a,b\in G$, and consider the two cosets $Na$ and $Nb$. Show that the set product $(Na)(Nb)$ is again a coset of $N$, and that we have $(Na)(Nb)=N(ab)$.
This shows that the set product is a binary operation on right cosets (and left cosets) of a normal subgroup $N$.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1an_2b$, then you should be able to write this, after some work, in either the form $n_3ab$ or the form $abn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
The next theorem should come as no surprise. We've already shown that given any subgroup $H$ of $G$, that every element of $H$ is in one of the cosets of $H$. We've also shown that the cosets of $H$ are disjoint. These two facts together show that we can partition $G$ into a disjoint union of cosets of $H$. We also know that the size of each coset matches the order of $H$. So if we have $r$ disjoint cosets $Ha_1$, $Ha_2$, $Ha_3$, ..., $Ha_r$, all of which have the same number of elements, then we should be able to use this information to show that the order of $H$ divides the order of the group. This fact is called Lagrange's theorem.
Problem 86 (Lagrange's Theorem Proof)
Prove Lagrange's Theorem.
Theorem (Lagrange's Theorem)
Suppose that $G$ is a finite group and that $H$ is a subgroup of $G$. Then the order of $H$ divides the order of $G$. In particular, we know that $|G|/|H|$ equals the number of distinct right (or left) cosets of $H$ in $G$.
We now have shown that the $|G|/|H|$ is precisely the number of cosets of $H$ there are in $G$. From a Cayley graph perspective, this is how many copies of $H$ are visible in the graph, as they are translated throughout the graph. The number of such cosets is called the index of $H$ in $G$, and written $|G:H|$.
Definition (Index of $H$ in $G$, or $|G:H|$)
If $H$ is a subgroup of $G$, then the index of $H$ in $G$, written $|G:H|$, is the number of distinct right (or left) cosets of $H$. Because of Lagrange's theorem, we know that $|G:H|=|G|/|H|$.
We'll now return to looking at when the left and right cosets of a subgroup agree, namely we'll be looking at normal subgroups. Let's first get ourselves a collection of subgroups that are normal.
Problem 87 (Some Normal Subgroups)
Prove the following facts.
- If $G$ is Abelian, then every subgroup of $G$ is normal.
- The center $Z(G)$ of any group $G$ is always a normal subgroup of $G$.
We are now ready to define a new group using the cosets of a normal subgroup. If $N$ is a normal subgroup of $G$, then we've already shown that the binary operation on the collection of cosets, defined by $(Na)(Nb)=N(ab)$, is well defined. Is this binary operation enough to forma a group? To say yes, we need to show that the operation is associative, that there is there an identity coset, and that every coset has an inverse coset. We're now ready to prove that the collection of cosets of a normal subgroup is actually a group, and we call this the factor group of $G$ by $N$, or the quotient group of $G$ by $N$, and we write $G/N$ to talk about this group of cosets.
Definition (Factor Group or Quotient Group of $G$ by $N$, or $G/N$)
Let $G$ be a group. Let $N$ be a normal subgroup of $G$. Then we define the factor group of $G$ by $N$, or the quotient group of $G$ by $N$, to be the set $G/N = \{Na\mid a\in G\}$, i.e the collection of right cosets of $N$ using the set product $(Na)(Nb)=N(ab)$ as the binary operation.
Problem 88 (The Quotient Group $G/N$ Is A Group)
Let $G$ be a group and let $N$ be a normal subgroup of $G$. Prove that the set $G/N$ is actually a group under the operation of coset products.
The next problem helps you refresh your memory about the definitions of homomorphism and order of an element. The problem has you show that if $f$ is a homomorphism from $G$ to $H$, then while $f$ may not preserve the order of elements in $a$, it has to send an element of order $n$ to an element whose order divides $n$. This must happen on an element by element basis. So if we know something about the order of $f(a)$, then we know that $|a|$ must be a multiple of $|f(a)|$.
Problem 89 (The order of $a$ is a multiple of the order of $f(a)$, or $|a|=k|f(a)|$)
Suppose that $f:G\to H$ is a homomorphism. Prove that if $a\in G$ has order $n$, show that $|f(a)|$ divides $n$, i.e. show that $|a|$ is a multiple of $|f(a)|$.
In addition to homomorphisms interacting nicely with elements and orders, even more can be said. In particular, if you know that there are $n$ things that map to the indentity $e$ in the codomain, then the homomorphism must carry exactly $n$ elements from the domain to each element of the codomain. For this reason, we say that a homomorphism is an $n$-to-one map. If you look back at last week's problems, you should see somewhere that we showed a result very similar to this, namely when we showed that the kernel of $f$ is a normal subgroup. Please look back at that problem before tackling this one.
Problem 90 (A homomorphism is an $n$-to-one map)
Let $f:G\to H$ be a homomorphism.
- Suppose that $\ker f$ has order $n$. If we know that $f(g)=h$ for some $g\in G$, prove that there are exactly $n$ different elements in $G$ that map to $h$, so we know that the preimage of $h$, namely $f^{-1}(h)$, is a set with $n$ elements. This shows that $f$ is an $n$-to-one map.
- Prove that $f$ is injective if and only if the kernel of $f$ is trivial, i.e. $\ker f = \{e\}$.
- Prove that if $f$ is surjective and the kernel of $f$ is trivial, then $f$ is an isomorphism.
Here are some comment's about these problems.
- This should follow without any additional work from a previous problem. Just figure out which problem.
- This is why in linear algebra we know that $A\vec x = b$ has a single solution if and only if the only solution to $A\vec x=\vec 0$ is $\vec x= 0$, which means the columns of $A$ are linearly independent. Finding the kernel, or null space, is crucial in linear algebra.
- This is why in linear algebra we know that when the kernel of a square matrix is trivial, then the matrix is invertible.
We now know that a homomorphism is an $n$-to-one map. This fact is basically a directly result of the fact that the kernel of a homomorphism is normal. The next exercise shows that every normal subgroup is the kernel of some homomorphism. This shows that studying normal subgroups is precisely equivalent to studying kernels of homomorphisms. We've actually been using the result below without every stating it formally. Given a Cayley graph, we can easily build a map from the Cayley graph to the corresponding identification graph using right cosets of $N$ by sending $a$ to $Na$. This exercise just has you shows that this map is indeed a homomorphism whose kernel is $N$.
Exercise (A Subgroup Is Normal If And Only If It Is The Kernel Of Some Homomorphism)
Prove that $N$ is a normal subgroup of $G$ if and only if $N$ is the kernel of some homomorphism $f:G\to H$ from $G$ to another group $H$.
Click to see a solution.
We already know that if $N$ is the kernel of a homomorphism, then it is normal. So one direction of this if and only if proof is complete.
If we know $N$ is normal, then we can let $H=G/N$ and define $f:G\to H$ by $f(g)=Ng$. This map is a homomorphism because we already showed that $f(ab)=N(ab)=(Na)(Nb) = f(a)f(b)$ when we showed that the set product is a binary operation on cosets of a normal subgroup. The kernel of this map is the set of elements $g\in G$ such that $f(g)=N$. This is precise the set of $g\in G$ such that $Ng=N$ which is true if and only if $g\in N$ by the properties of cosets. Hence the kernel of this map is $N$.
This next problem has you practice using Lagrange's theorem. Both facts in the problem should follow immediately from applying Lagrange's theorem and another observation. These facts are often considered corollaries of Lagrange's theorem.
Problem 91 (The Order Of An Element Divides The Order Of A Group)
Let $G$ be a finite group. Use Lagrange's theorem to prove the following two corollaries.
- Let $a\in G$. The order of $a$ divides the order of $G$.
- If $|G|=p$ for some prime $p$, then $G$ is cyclic.
We are now ready to state and prove what mathematicians call the first isomorphism theorem. We've seen the following result several times before, without every fully stating it. When we consider the dihedral group of order 8 and let $N$ be the set of rotations, the identification graph looked a lot like $\mathbb{Z}_2$. The map $f:D_8\to \mathbb{Z}_2$ defined by $f(g)=0$ if $g$ is a rotation and $f(g)=1$ if $g$ is a flip, is a homomorphism from $D_8$ to $\mathbb{Z}_2$. The kernel of this homomorphism is precisely the rotations $N$. So the factor group $G/N$ consists of two cosets and is isomorphic to $\mathbb{Z}_2$. We now formally state the first isomorphism theorem.
Here's a formal statement of the first isomorphism theorem. It's slightly different than the text's, and we'll talk about why it's different in class. The version in the text involves more notation, but is essentially equivalent to this version. The key you need to proving this theorem comes from some of the earlier problems today (which problem has you show that something is an isomorphism?).
Problem 92 (The First Isomorphism Theorem Proof)
Prove the First Isomorphism Theorem.
Theorem (The First Isomorphism Theorem)
Let $f:G\to H$ be a surjective homomorphism with kernel $K$. Because we know that $f(x)=f(y)$ for any $y\in Kx$ (elements in the same coset of the kernel have the same image under $f$), then we can define a map $\phi:G/K\to H$ by defining $\phi(Kg)=f(g)$. This map $\phi$ is always an isomorphism.
We'll start using this theorem almost every day from here on out, as this is one of the biggest ideas in abstract algebra. For now, just make sure you can prove it.
Exercise (The Integers Under Addition Are Isomorphic To The Positive Integers Under Multiplication)
The set $\mathbb{R}^+$ is the set of positive real numbers. Consider the two groups $G=(\mathbb{R},+)$ and $H=(\mathbb{R}^{+},\cdot)$. Show that these two groups are isomorphic by showing that the exponential function $f(x)=\exp(x)$ is a group isomorphism.
Click to see a solution.
You could prove this by showing that the map is a homomorphism, and that it is a bijection by producing the inverse (namely $g(x)=\ln x$) and proving that it is an inverse. We've already done this in class.
Let's instead use the first isomorphism theorem. We know that $\exp(a+b)=\exp(a)\exp(b)$ high school algebra, so $f$ is a homomorphism. Given $y\in \mathbb{R}^{+}$, we let $x=\ln y$ and then $\exp(x)=y$, so the map is surjective. The only value such that $f(x)=1$ is $x=0$, so the kernel is $K=\ker f = \{0\}$. We could stop here and note that this means $f$ is 1 to 1, i.e. injective, and hence a bijection. Alternately, we could notice that $G/K=G$ (the identification graph of $G/K$ is the same as $G$ since $|K|=1$) and the first isomorphism theorem states that $f:G/K\to H$ is an isomorphism.
One of the reasons we care about factor groups is that we can often determine information about large, possibly hard to explore groups, by taking information from the factor group and pulling it back to the larger group. We know that the map $f:G\to G/N$ defined by $f(g)=Ng$ is a homomorphism, so we can often obtain information about $G$ by using this homomorphism to pull back information from $G/N$. The next problem has you show an example of this, namely that if you can find an element of order $k$ in $G/N$, then there must be an element of this order as well in $G$. Your work from last time should make this problem quite fast, provided you remember that $\langle a\rangle$ is a cyclic group, and as such is isomorphic to $\mathbb{Z}_{|a|}$, which we understand quite well.
Problem 93 (If A Factor Group $G/N$ Has An Element Of Order $k$ Then So Does $G$)
Suppose that $N$ is a normal subgroup of a finite group $G$ and that $Na$ has order $k$ as an element of $G/N$. Prove the following two facts.
- The order of $a$ in $G$ is a multiple of the order of $Na$ in $G/N$.
- There exists an element $b\in G$ that has order $k=|Na|$.
In other words, if a factor group has an element of order $k$, the the original group before factoring must have an element of order $k$ as well.
We have already shown that $Ha=aH$ for every $a\in G$ if and only if $aHa^{-1}=H$ for every $a\in G$. So one way to prove that a subgroup is normal is to prove that $aHa^{-1}=H$ for every $a\in G$. However, this requires that for each $a\in G$ you show both $aHa^{-1}\subseteq H$ and $H\subseteq aHa^{-1}$. The next problem simplifies this process even more. It says that if you know $aHa^{-1}\subseteq H$, then the other set inclusion must follow immediately.
Problem 94 (The Normal Subgroup Test)
Suppose that $G$ is a group and $H$ is a subgroup of $G$. Prove that $H$ is a normal subgroup of $G$ if and only if $xHx^{-1}\subseteq H$ for all $x\in G$.
How does normality behave when we look at subgroups? The following problem has you show that if you know $N$ is normal in $G$, and $N$ lies in some subgroup $B$ of $G$, then $N$ must be normal in $B$ as well. However, if we know $N$ is normal in $B$, and $B$ is normal in $G$, this does not guarantee that $N$ is normal in $G$. In symbols, we have $N\leq B\leq G$ and $N\trianglelefteq G$ implies $N\trianglelefteq B$, but we cannot say that $N\trianglelefteq B\trianglelefteq G$ implies $N\trianglelefteq G$. Being normal in a large group is enough to pass down to subgroups, but being normal in a subgroup is not enough to force normality in a larger group.
Problem 95 (Subgroups And Normality)
Suppose that $G$ is a group and that $A\leq B\leq G$.
- If $A$ is normal in $G$, prove that $A$ is normal in $B$.
- If $A$ is normal in $B$ and $B$ is normal in $G$, must $A$ be normal in $G$? Find a counter example to this.
The next problem has you show that when you compute factor groups, lots of properties pass immediately from $G$ to $G/N$. In particular, if $G$ is Abelian then $G/N$ is Abelian. Also, if $G$ is cyclic, then $G/N$ is cyclic. Many other properties follow as well.
Problem 96 (Factor Groups Preserve Being Cyclic And Abelian)
Suppose that $N$ is a normal subgroup of $G$.
- If $G$ is cyclic, prove that $G/N$ is cyclic.
- If $G$ is Abelian, prove that $G/N$ is Abelian.
The previous problem is an application of the bigger idea connected to homomorphism. Namely that the image of an Abelian group is Abelian, and the image of a cyclic group is cyclic.
Problem 97 (Images Of Abelian And Cyclic Groups)
Let $f:G\to H$ be a homomorphism. We have already shown that the image of $f$, written $f(G)$, is a subgroup of $H$.
- Prove that if $G$ is Abelian, then $f(G)$ is Abelian.
- Prove that if $G$ is cyclic, then $f(G)$ is cyclic.
How do the properties of Abelian and cyclic behave when combined with external direct products?
Problem 98 (External Direct Products Of Abelian And Cyclic Groups)
Suppose that $G$ and $H$ are groups.
- Prove or disprove: If both $G$ and $H$ are Abelian, then $G\oplus H$ is Abelian.
- Prove or disprove: If $G\oplus H$ is Abelian,then both $G$ and $H$ are Abelian.
- Prove or disprove: If both $G$ and $H$ are cyclic, then $G\oplus H$ is cyclic.
- Prove or disprove: If $G\oplus H$ is cyclic, then both $G$ and $H$ are cyclic.
The next problem has you prove Fermat's little lemma. We already conjectured this earlier in the semester when we noticed that if $p$ is a prime, then regardless of which $a$ we pick from $U(p)$, we must always have $a^{p-1}=1$. Sometimes, this is the order of $a$, whereas sometimes it is not. First, let's look at another conjecture we made earlier in the semester, to get us back into thinking about the $U$ groups.
Exercise (The Last Element Of UN Is Always Its Own Inverse)
Pick an integer $n$ greater than 1. Prove that $(n-1)\in U(n)$ is always its own multiplicative inverse.
Click to see a solution.
Notice that $(n-1)\pmod n = (-1)\pmod n$, which means $(n-1)^2\pmod n = (-1)^\pmod n = 1\pmod n$. This shows that the order of $n-1$ is 2, and also that $n-1$ is its own inverse.
Problem 99 (Fermat's Little Lemma)
Let $G$ be a finite group. Use Lagrange's theorem to prove the following two corollaries.
- We have $a^{|G|}=e$ for every $a\in G$.
- [Fermat's Little Lemma] Let $p$ be a prime and suppose $a\in U(p)$. Then we must have $a^p\pmod p=a$. (Hint: What is the order of $U(p)$?)
Using Fermat's little lemma and/or Lagrange's theorem, you should be able to rapidly prove the next result.
Exercise (The Order Of A In UP Divides P-1)
Let $p$ be a prime. Let $a\in U(p)$. Then $|a|$ divides $p-1$.
Click to see a solution.
There are several ways to prove this result.
- Since we know $a^p\pmod p = a$, we konw $a^{p-1}\pmod p = 1$. We know that $a^k=e$ in any group only when $k$ is a multiple of the order of $|a|$, so this means $k=p-1$ is a multiple of $|a|$.
- We now that $|U(p)|=p-1$. Hence every subgroup of $U(n)$, in particular $\left<a\right>$, must have an order that divides $p-1$. Since we know $|a|=|\left<a\right>|$, we know that $|a|$ divides $p-1$.
Because we are working with homomorphisms quite a bit in our work, we see the notation $f(g)=g$ quite a bit. We have also seen the notation $f^{-1}(h)$, but because homomomorphisms are not necessarily injective, this is not the inverse of $f$ applied to $h$. We have to remember that when we write $f^{-1}(h)$ we are talking about a set, namely the set of all $x\in G$ such that $f(x)=h$. We are not talking about a single $g$ so that $f(g)=h$. The notation $f^{-1}(h)$ represents the preimage (or inverse image) of $\{h\}$ under $f$. Here's a reminder of the formal definition.
Definition (Preimage Or Inverse Image)
If $f:A\to B$ and $C\subseteq B$, then the preimage of $C$ under $f$ is the set of all $a\in A$ such that $f(a)\in C$, and we write the preimage of $C$ under $f$ as $$f^{-1}(C)=\{a\in A\mid f(a)\in C\}.$$ When $C=\{c\}$ contains a single element, we often write the preimage of $C$ under $f$ as $f^{-1}(c)$ instead of using the more formal cumbersome notation $f^{-1}(\{c\})$.
Preimages and subgroups interact in a very nice way, namely homomorphisms preserve subgroups when computing inverse images. Next time we'll show that preimages preserve normality.
Problem 100 (The Preimage Of A Subgroup Under A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism. Let $B$ be a subgroup of $H$. Let $A$ be the preimage of $B$, namely $$A=f^{-1}(B)=\{g\in G\mid f(g)\in B\}.$$ Show that $A$ is a subgroup of $G$.
Problem 101 (Homomorphisms Preserve Normal Subgroups)
Suppose that $f:G\to H$ is a homomorphism. Use The Normal Subgroup Test to prove the following:
- If $N$ is normal in $G$, then $f(N)$ is normal in $f(G)$.
- If $B$ is normal in $H$, then $f^{-1}(B)$ is normal in $G$.
At this point, we've proved quite a large collection of facts about homomorphisms and what they preserve. I strongly suggest that you look at pages 202-204 of your text to see a list of these properties. Then read the remarks on page 204.
The following two facts follow immediately from using the properties of homomorphisms. The first fact shows that any time you have a subgroup that contains half the elements of the group, that subgroup must be a normal subgroup.
Problem 102 (Subgroups Of Index 2 Are Normal)
Suppose that $H$ is a subgroup of $G$ with index $|G:H|=2$. Recall that the index of $H$ in $G$ is the number of distinct cosets of $H$ in $G$.
- Build a surjective homomorphism from $G$ to $\mathbb{Z}_2$.
- Show that $H$ is normal in $G$.
This next fact shows that any time you have subgroup in a factor group $G/N$, it corresponds to a subgroup $H$ in $G$ that contains $N$.
Problem 103 (Subgroups Of A Quotient Group Correspond To Subgroups Of The Original Group)
Suppose that $N$ is a normal subgroup of $G$ and that $B$ is a subgroup of $G/N$. Prove the following:
- There exists a subgroup $H\leq G$ such that $H/N=B$.
- If we know that $n=|N|$ and $m=|B|$ (so $n$ is the order of $N$ in $G$, and $m$ is the order of $B$ in $G/N$), then $G$ must have a subgroup $H$ of order $nm$.
As a suggestion, consider the homomorphism $f:G\to G/N$ given by $f(g)=Ng$ and use some properties of homomorphisms.
To tackle the next problem, you'll want to rely on the fact that $|(g,h)|=\text{lcm}(|g|,|h|)$, together with the fact that two integers are relatively prime if and only if their product is their least common multiple.
Problem 104 (A Direct Product Of Cyclic Groups Is Cyclic If And Only If The Groups Have Relatively Prime Orders)
Suppose that $G$ and $H$ are finite cyclic groups. Prove that $G\oplus H$ is cyclic if and only if $|G|$ and $|H|$ are relatively prime.
Exercise (A Direct Product Of Cyclic Groups Is Cyclic If And Only If The Groups Have Relatively Prime Orders)
Use induction to extend the previous result to the external direct product of $n$ cyclic groups. So prove that if $G_1,G_2,\ldots,G_n$ are $n$ cyclic groups, then $G_1\oplus G_2\oplus \cdots\oplus G_n$ is cyclic if and only if $|G_i|$ and $|G_j|$ are relatively prime when $i\neq j$.
Click to see a hint.
This exercise require that you use induction on an "if $p$ then $q$" statement. In addition, the $q$ part of the statement involves an if and only if. You must be very careful how you tackle this problem.
Problem 105 (An Isomorphism From $U(st)$ To $U(s)\oplus U(t)$ When $s$ And $t$ Are Relatively Prime)
Recall that $\varphi$, the Euler-phi function is defined by $\varphi(n)=|U(n)|$, the order of $U(n)$. Suppose $n=st$ where $s$ and $t$ are relatively prime. In this problem you'll show that $\varphi(st)=\varphi(s)\varphi(t)$.
- Show that $f:U(st)\to U(s)\oplus U(t)$ defined by $f(x)=(x\mod s,x\mod t)$ is an isomorphism.
- Why does $\varphi(st)=\varphi(s)\varphi(t)$ when $s$ and $t$ are relatively prime?
- Use the results above to compute $\varphi(17\cdot 19)$ and $\varphi(15\cdot 63)$.
It's time to use the power of factor groups, together with induction, to prove the first of many powerful theorems that apply to finite groups. The key lies in the fact that the order of a factor group $G/N$ will always be less than the order of $G$, provided $N$ is not trivial. This means that if we use induction on the order of a group, then if we can use a factor group to pull back information to a larger group, induction will provide us with precisely the tool we need to prove some really powerful theorems about groups.
The next theorem is often called Cauchy's theorem (for Abelian groups). The more general version of Cauchy's theorem states that if $p$ is a prime that divides the order of the group, then $G$ must have an element of order $p$. Because it's an Abelian group, every subgroup is normal, which means we can quickly create factor groups any time we obtain a subgroup. If we remove the Abelian condition, then we have to prove that a subgroup is normal before we can create a factor group. The Abelian condition is a simplifying assumption, which can be removed with much more work.
Problem 106 (Abelian Groups Have An Element Of Order $p$ For Every Prime That Divides The Order Of The Group)
Let $G$ be an Abelian group and let $p$ be a prime. Prove that if $p$ divides the order of $G$, then there exists $a\in G$ with order $p$.
Hint: This problem is done by induction on the order of $G$.
For each integer $k\geq 2$, let $P(k)$ be the statement, "For every positive integer $n<k$, if $|G|=n$ and $p$ divides $|G|$ then $G$ has an element of order $p$." Use induction to prove that $P(k)$ is a true statement for every integer $k\geq 2$. This will require you to do two things.
- Is the statement $P(2)$ true? Is the statement $P(3)$ true?
- If you assume for some specific $k\geq 2$ that the statement $P(k)$ is true, then prove that the statement $P(k+1)$ is true. To prove $P(k+1)$ is a true statement, you have to prove that if $n<k+1$ and $|G|$ has order $n$ with $p$ dividing $G$, then $G$ has an element of order $p$. This is quite a lot of facts to prove. However, the induction assumption should prove every single one of them instantly except for when $n=k$. So you must show that if $|G|=k$ and $p$ divides $|G|$, then $G$ has an element of order $p$. You know for sure that $G$ has an element of some order other than 1, say $m=|a|$, which means that it has an element $b$ of some prime order $q$ (why?). If $q=p$ we're done. Otherwise, consider the factor group $G/\left<b\right>$. What is the order of $G/\left<b\right>$? Does $p$ divide $G/\left<b\right>$? What does the induction assumption then tell you? How does problem 103 help?
For more problems, see AllProblems

