Please Login to access more options.
Problem 7 (Automorphisms Of A Square 2)
Again consider the graph $\mathcal{G} = (V,E)$ shown below with vertex set $V = \{1,2,3,4\}$ and edges $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$
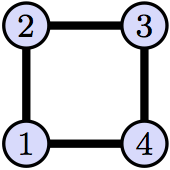
Recall that set of all automorphisms of $\mathcal{G}$ is written $\aut(\mathcal{G})$. We listed all the elements in this set in problem AutomorphismsOfASquare. Determine if each statement below is true or false. Make sure you justify your answers.
- There is an automorphism $a\in \aut(\mathcal{G})$ such that $a^2=a\circ a$ (the composition) is the identity automorphism, but $a$ is not the identity.
- There is an $a\in \aut(\mathcal{G})$ such that $a^3=a\circ a\circ a$ is the identity but $a$ is not the identity.
- There is an $a\in \aut(\mathcal{G})$ such that every other $b\in \aut(\mathcal{G})$ is of the form $b=a^n$ for some $n$. [Hint: for each element in $\aut(G)$, find the smallest $n$ such that $a^n=id_V$. ]
- For every $a,b\in \aut(\mathcal{G})$, we have $a\circ b = b\circ a$.
The following pages link to this page.
