20170915

Please Login to access more options.

Today

Definition (Permutation)

Let $X$ be a set. A $\textdef{permutation}$ of $X$ is a bijection from $X$ to $X$, so it's a function from $X$ into $X$ that is both one-to-one and onto. We can think of a permutation of $X$ as a way of rearranging the elements in $X$. The identity permutation is the permutation $id_X:X\to X$ defined by $id_X(x)=x$.

Problem 5 (Number Of Permutations)

Given finite set $X$ with $n$ elements, how many permutations are there of $X$?

• Show that if $X=\{1\}$, then there is only one permutation of $X$.
• Show that if $X=\{1,2\}$, then there are two permutations of $X$. List them.
• Make a list of all permutations of $X=\{1,2,3\}$, and then of $X=\{1,2,3,4\}$. What pattern do you see?
• Make a conjecture about the number of permutation of $X$ if $|X|=n$. Then prove your conjecture.

Definition (Automorphism Of A Graph)

An $\textdef{automorphism of a graph}$ is a permutation $\sigma$ of the set of vertices such that two vertices $x$ and $y$ form an edge if and only if $\sigma(x)$ and $\sigma(y)$ form an edge. The $\textdef{automorphism group of a graph}$ is the set of all automorphisms of the graph. If $\mathcal{G}$ is a graph, its automorphism group is denoted $\aut(\mathcal{G})$.

Problem 6 (Automorphisms Of A Square)

Consider the graph $\mathcal{G} = (V,E)$ drawn below. The vertex set is $V = \{1,2,3,4\}$ and the set of edges is $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$

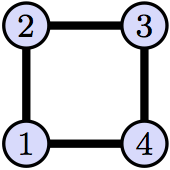
Write down all the automorphisms of $\mathcal{G}$ (there are more than 4, but less than 10). Explain how you know you have listed every automorhpism of $\mathcal{G}$.

This problem continues in AutomorphismsOfASquare2.

Problem 7 (Automorphisms Of A Square 2)

Again consider the graph $\mathcal{G} = (V,E)$ shown below with vertex set $V = \{1,2,3,4\}$ and edges $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$

Recall that set of all automorphisms of $\mathcal{G}$ is written $\aut(\mathcal{G})$. We listed all the elements in this set in problem AutomorphismsOfASquare. Determine if each statement below is true or false. Make sure you justify your answers.

1. There is an automorphism $a\in \aut(\mathcal{G})$ such that $a^2=a\circ a$ (the composition) is the identity automorphism, but $a$ is not the identity.
2. There is an $a\in \aut(\mathcal{G})$ such that $a^3=a\circ a\circ a$ is the identity but $a$ is not the identity.
3. There is an $a\in \aut(\mathcal{G})$ such that every other $b\in \aut(\mathcal{G})$ is of the form $b=a^n$ for some $n$. [Hint: for each element in $\aut(G)$, find the smallest $n$ such that $a^n=id_V$. ]
4. For every $a,b\in \aut(\mathcal{G})$, we have $a\circ b = b\circ a$.

Problem 8 (Automorphisms Of A Directed Square)

Consider the directed graph $\mathcal{G} = (V,A)$ shown below with vertex set $V = \{1,2,3,4\}$ and arrows (directed edges) $$A = \{(1,2),(2,3),(3,4),(4,1)\}.$$

1. How would you define an automorphism of a directed graph?
2. List all the automorphisms of this directed graph. You should have 4.
3. Is there is an automorphism $a\in \aut(\mathcal{G})$ such that $a^2=a\circ a$ (the composition) is the identity automorphism, but $a$ is not the identity?
4. Is there is an $a\in \aut(\mathcal{G})$ such that $a^3=a\circ a\circ a$ is the identity but $a$ is not the identity?
5. Is there is an $a\in \aut(\mathcal{G})$ such that every other $b\in \aut(\mathcal{G})$ is of the form $b=a^n$ for some $n$?
6. For every $a,b\in \aut(\mathcal{G})$, do we have $a\circ b = b\circ a$?

Problem 9(Simple Shift Repetition)

Let's now devise a way to not only encrypt a message, but also keep track of who has seen the message? There are several ways to do this. Let's look at an example that involves repeated application of the same encrpytion key. For this example, let's use the encryption key $\phi_4:S\to S$ (the simple shift permutation that shifts right 4).

A group of military commanders decide to send messages using a message chain. The message passes sequentially from one person to the next, where at each stage they apply the encryption key to the ciphertext before sending it on. If I want to send the plain text message $attackatdawn$, then I'd send the message $exxegoexhear$ to the person after me in the chain. This person would decipher the text using $\phi_4^{-1}$ (shift left 4), and then apply $\phi_4$ to the cipher text $exxegoexhear$ and then send the ciphertext $ibbiksibliev$ to the person after them in the chain. This would repeat until the message made it to every commander.

1. You receive the cipher text $skkzgzkomnz$. What is the plain text message? How many people have seen this message?
2. How many commanders can we include in this encryption scheme and still tell who sent the message?
3. If we use $\phi_5$ instead of $\phi_4$, how many commanders can we include in this encryption scheme and still tell who sent the message?
4. Is there an encryption key $\phi_n$ so that $\phi_n^2=\phi_0$. In other words, is there an encryption key $\phi_n$ that will only allow up to two commands to be in the chain?

Problem 10 (Cryptography Reading Assignment)

Download the free open source book Abstract Algebra: Theory and Applications by Thomas W. Judson. See http://abstract.ups.edu/. (For a direct link use http://abstract.ups.edu/download/aata-20160809.pdf .)

1. Read pages 76-81. This is chapter 7, Introduction to Cryptography. It's OK if you don't understand all the notation.
2. Come with at least three questions about parts of the reading you would like to understand more about.

It's OK if you don't understand all of the reading. He uses some theorems and notation that we have not yet covered. If you want to know more about how some of the things worked in the reading, please make sure you ask a question.

Once we have a set of permutations, we'd like to be able to combine them to get new permutations. The previous problem used repetition on simple shift permutations of the alphabet to obtain additional permutations. The next problem has you show that the composition of any finite collection of permutations on a set is always a permutation.

Theorem (The Composition Of Permutations Is A Permutation)

Let $X$ be a set. Suppose that $\sigma_1, \sigma_2, \ldots,\sigma_k$ are permutations of $X$. Then the composition $\sigma_1\circ \sigma_2\circ \ldots\circ \sigma_k$ is a permutation of $X$.

Problem 11 (The Composition Of Permutations Is A Permutation)

Prove theorem (The Composition Of Permutations Is A Permutation). As some reminders, you may use the following facts that you proved in either Math 301 or Math 340. You may use these facts without proof.

• The composition of two injective functions is injective.
• The composition of two surjective functions is surjective.
• A function is a bijection if it is both injective (1 to 1) and surjective (onto). Hence, the composition of two bijective functions is a bijection.
• You might find induction helps you get from a composition of two bijective functions is bijective to the composition of $n$ bijective functions is bijective.

Remember, anytime you see a new theorem, definition, idea, etc., start by making an example, and a non example. If someone in class wants to see an example, I'd love to have you share your work there.

Problem 12 (Do We Need The Associative Law)

In this problem, your job is to explain each step in the process of solving $2x=3$ for $x$. Try to break each part of your computation down into the most basic processes. The only two operations we have on the real numbers are addition and multiplication. Subtraction and division are inverse operations, so rather than saying "divide by 2", you would multiply by the multiplicative inverse of 2. As always, write your solution using complete sentences.

• If you did not use the associative law of multiplication in your work, then go back through your work. It should be there somewhere.
• Did you use the commutative law of multiplication in your work? If you did, make sure you pinpoint where you did. It is possible to solve this problem without the commutative law.
• You might try to justify this as follows:
  First divide both sides of $2x=3$ by 2. Then cancel the 2's on the left side of the equation and we have $x=3/2$.

For more problems, see AllProblems