Please Login to access more options.
Problem 30 (Cayley Graphs Of Two Automorphism Groups)
Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.
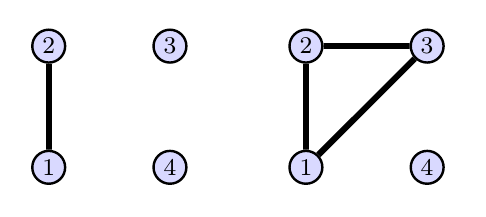
We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).
- For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
- For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.
The following pages link to this page.
