Please Login to access more options.

---

Today

« October 2017 »
Sun	Mon	Tue	Wed	Thu	Fri	Sat
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

---

If $X$ is a set, and $S$ is a set of permutations of $X$, then we can create a Caley graph for the span of $S$. Here's a formal definition.

Definition (Cayley Graph Of A Span Of Permutations)

Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:

1. The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
2. Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
3. For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.

Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.

We've done this with several automorphism groups of graphs, as well as simple shift permutation groups.

Problem 30 (Cayley Graphs Of Two Automorphism Groups)

Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.

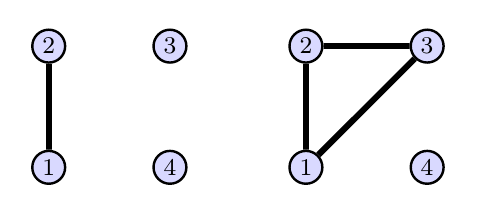
We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).

1. For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
2. For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.

---

If $X$ is a set, and $S$ is a set of permutations of $X$, then we already know how to create the span of $S$. In general, the span of $S$ will include more permutations than what we started with. However, sometimes we won't be able to obtain any new permutations by spanning $S$. When this happens, we say that the set of permutations is closed (under function composition). Here's a formal definition.

Definition (A Closed Set Of Permutations)

We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.

The next problem has you prove some relationships between a set of permutations $S$ and its span.

Problem 32 (Relationship Between S And Its Span)

Let $S$ be a set of permutations of $X$.

1. Prove that $S\subseteq \text{span}(S)$. In other words, we know that $S$ is always contained in its span; the span might be larger.
2. Prove that if $\text{span}(S)\subseteq S$, then $S$ is closed.
3. If $T\subseteq S$, then show that $\text{span}(T)\subseteq\text{span}(S)$.

---

Definition (Integer Linear Combination Of Integers)

Let $a_1, a_2, \ldots, a_k$ be $k$ integers.

• An integer linear combination of these integers is an expression of the form $$c_1a_1+c_2 a_2+ \cdots+c_k a_k$$ where each coefficient $c_i$ is an integer.
• The span of the set of integers $\{a_1, a_2, \ldots, a_k\}$ is the set of all possible integer linear combinations of these integers, namely $$\text{span}(\{a_1, a_2, \ldots, a_k\})=\text{span}(a_1, a_2, \ldots, a_k)=\{c_1a_1+c_2 a_2+ \cdots+c_k a_k\mid c_i\in \mathbb{Z} \text{ for }1\leq i\leq k\}.$$ For ease of notation, we'll often leave off the set notation when spanning a set of integers.
• If the set $S$ of integers is infinite, then we still define the span of $S$ to be the set of all integer linear combinations of integers in $S$. Hence we know $x\in S$ if and only if there exists a natural number $k$ such that $x=c_1a_1+c_2 a_2+ \cdots+c_k a_k$ where $a_i\in S$ and $c_i\in \mathbb{Z}$ for $1\leq i\leq k$.
• When there are only two integers, we'll often use $a$ and $b$ as the integers, and $s$ and $t$ as the coefficients. So the set of all integer linear combinations of $a$ and $b$ is $$\text{span}(a,b) = \{sa+tb\mid s,t\in\mathbb{Z}\}.$$

Problem 33 (Integer Linear Combination Practice)

Complete the following.

1. Compute the span of $3$, i.e. make a list of the elements in this set. In general, what is the span of a single integer $a$? (We know it by a different name.)
2. What is $\text{span}(4,6)$? List the elements. Find a single number $a$ so that $\text{span}(a)=\text{span}(4,6)$.
3. What is $\text{span}(4,5)$?
4. Let $S=\{a_1,a_2,\ldots,a_k\}$ be a set of integers. Show that if $c\in \text{span}(S)$, then so is every multiple of $c$.

---

We've seen a lot of relationships in class about modular arithmetic, inverses mod n, simple shift encryption schemes, and more. The next problem makes a connection between some of these. We'll connect it to even more next time.

Problem 34 (When Does An Integer Have A Modular Multiplicative Inverse)

Let $a$ and $n$ be integers, with $n>1$. Show that the following are equivalent.

1. The integer $a$ has a multiplicative inverse mod $n$
2. We have $1\in \text{span}(a,n)$. In other words, we can write 1 as a linear combination of $a$ and $n$.
3. We have $\text{span}(a,n)=\mathbb{Z}$. Remember that $\text{span}(a,n) = \{sa+tn\mid s,t\in\mathbb{Z}\}.$

Remember, to show that three things are equivalent you must show that each implies the other. One way to do this is show that 1 implies 2, then show that 2 implies 3, and then show that 3 implies 1. Then each implies the other.

---

The two problems above, together with much of our work from the previous weeks, leads us to one of the biggest theorems in number theory. We'll prove this theorem later in the semester.

Theorem (The GCD Theorem)

Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.

Corollary (When Are Two Numbers Relatively Prime)

Two nonzero numbers $a$ and $b$ are relatively prime (i.e. their greatest common divisor is 1) if and only if there exists $s$ and $t$ such that $sa+tb=1$.

Problem 35 (Connecting Multiples And Spans Of Integers)

Suppose that $a$ and $b$ are integers.

1. Prove that if $a$ is a multiple of $b$, then we must have $\text{span}(a)\subseteq\text{span}(b)$.
2. Is the converse of the statement above true or false? Make sure you prove your result.

---

Problem 36 (Permutations of $U(n)$)

Suppose $n$ is an integer greater than 1 and let $X=U(n)$, so the set of integers mod $n$ that have a multiplicative inverse mod $n$. For each $a\in U(n)$, we can define a permutation of $U(n)$ by $f_a(x)=xa\pmod n$ for each $x\in U(n)$. This problem asks you to show that this is indeed a permutation of $U(n)$. This requires that you show the following:

1. For each integer $n\geq 2$, show that if $a\in U(n)$ and $x\in U(n)$, then the product $f_a(x)=xa\pmod n\in U(n)$. This shows that $f_a:U(n)\to U(n)$ is a map from $U(n)$ to $U(n)$.
2. Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is one-to-one. (As a reminder, one-to-one means that if $f_a(x)=f_a(y)$, then $x=y$.)
3. Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is onto. (As a reminder, onto means that if $y\in U(n)$, then there exists $x\in U(n)$ such that $f_a(x)=y$.)

---

Problem 37 (Three Similar Cayley Graphs From Different Contexts)

This problem asks you to draw 3 Cayley graphs. Each Cayley graph should only have 4 vertices.

1. Draw a Cayley graph for the set $H_4$ of simple shift permutations of $X=\{1,2,3,4\}$ using the generating set $S=\{\phi_1\}$.
2. Then draw a Cayley graph for the span of the permutation $(1,4,3,2)$, which we wrote in disjoint cycle notation.
3. Then draw a Cayley graph for $\{f_a\mid a\in U(5)\}$ using the generating set $S=\{f_2\}$. Remember that $f_a$ is a permutation of $U(5)$ defined by $f_a(x)=xa\pmod 5$.
4. What do you notice about these Cayley graphs?

---

The three graphs from the previous problem look very similar, so much so that we could obtain one from the other if we just relabeled the vertex sets. This suggests that in some sense these graphs are the same. We now introduce a formal way to talk about when two graphs are the same.

Definition (Isomorphic Graphs)

Let $G$ and $H$ be two graphs, where we use $V(G)$ and $V(H)$ to denote the vertex sets. A function $f:V(G)\to V(H)$ is called an isomorphism of graphs $G$ and $H$ if $f$ is a bijection and $\{x,y\}$ is an edge of $G$ if and only if $\{f(x),f(y)\}$ is an edge of $H$ (see Wikipedia).

• We call this function $f$ an isomorphism because it "preserves the edge structure" in the graph. In general the word isomorphism refers to a bijection that preserves some kind of structure.
• If there exists an isomorphism of graphs between $G$ and $H$, then we say that $G$ and $H$ are isomorphic.
• If $G$ and $H$ are directed graphs, then an isomorphism of directed graphs would preserve the arrow structure.
• If the directed graphs $G$ and $H$ are colored, then an isomorphism also preserves the color structure, in the sense that $(a,b)$ and $(c,d)$ share the same color if and only if $(f(a),f(b))$ and $(f(c),f(d))$ share the same color.

Problem 38 (Introduction To Cayley Graph Isomorphisms)

Let $H_6 = \{\phi_0,\phi_1,\ldots,\phi_5\}$ be the set of simple shift permutations on an alphabet with 6 letters. Let $K=\{f_a\mid a\in U(7)\}$ be the set of permutations $f_a:U(7)\to U(7)$ defined by $f_a(x)=xa\pmod 7$. Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$.

1. Draw the Cayley graph of $H_6$ generated by $\{\phi_1\}$. Then draw the Cayley graph of $K$ generated by $\{f_3\}$. Finally show that the function $g:H_6\to K$ defined by $$ g(\phi_0)=f_1, g(\phi_1)=f_3, g(\phi_2)=f_2, g(\phi_3)=f_6, g(\phi_4)=f_4, g(\phi_5)=f_5, $$ is an isomorphism of Cayley graphs.
2. Draw the Cayley graph of $H_6$ generated by $\{\phi_2, \phi_3\}$. Then draw the Cayley graph of $K$ generated by $\{f_2,f_6\}$. Do you believe these two Cayley graphs are isomorphic? You can just give a heuristic argument, rather than a formal proof.
3. Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$. We've already shown this set has 6 permutations. Draw a Cayley graph of $S_3$ generated by the permutations $(1,2,3)$ and $(1,2)$. Do you think that this Cayley graph is isomorphic to any of the Cayley graphs above? Why?

---

---

For more problems, see AllProblems