Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
October 2
Please complete the following problem, carried over from last time.
Problem 28 (Computing Multiplicative Inverses For Small N)
To use modular arithmetic in matrix encryption, we must be able to find the modular multiplicative inverse of $a \mod n$. For each $n\leq 13$ and $a\in \mathbb{Z}_n$, we now compute the inverse of $a\mod n$ or explain why it does not have one.
- Why does $0\mod n$ never have an inverse?
- What is the multiplicative inverse of $1\mod n$?
- For $n=3$, what is the multiplicative inverse of $a=2$.
- For $n=4$, show that 2 does not have an inverse by computing $2\cdot 0$, $2\cdot 1$, $2\cdot 2$, and $2\cdot 3$ all modulo $4$. What is $3^{-1}\mod 4$?
- For each $n$ between 5 and 13, create a table that shows the inverse of each $a\in \mathbb{Z}_n$. List the elements of $\mathbb{Z}_n$ along the top row, and beneath each element list the multiplicative inverse, or cross off the number if there is no multiplicative inverse.
When you are done you should have a list of the elements of $U(n)$ for each $n$ up to 13, as well as the inverse of each element in $U(n)$. Do you see any patterns?
For $n=9$, you should obtain a table somewhat similar to the following table.
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $a^{-1}$ | x | 1 | 5 | x | 7 | 2 | x | 4 | 8 |
If $X$ is a set, and $S$ is a set of permutations of $X$, then we can create a Caley graph for the span of $S$. Here's a formal definition.
Definition (Cayley Graph Of A Span Of Permutations)
Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.
We've done this with several automorphism groups of graphs, as well as simple shift permutation groups.
Problem 30 (Cayley Graphs Of Two Automorphism Groups)
Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.
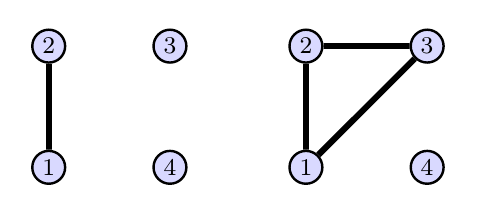
We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).
- For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
- For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.
The set $X$ does not have to be finite to draw a Cayley graph, nor does $\text{span}(S)$.
Problem (An Infinite Cayley Graph)
In each scenario below, you should draw a Cayley graph.
- Let $X=\mathbb{Z}$, an infinite set. Consider the permutation $\phi_1:\mathbb{Z}\to \mathbb{Z}$ defined by $\phi_1(x)=x+1$. This permutation shifts elements in $\mathbb{Z}$ right one, with no wrap around. If we let $S=\{\phi_1\}$, give a rough sketch of the Cayley graph of $\text{span}(S)$. It's a rough sketch of the graph because there are infinitely many vertices.
- How would you change your graph in part 1 if instead you used $S=\{\phi_2,\phi_3\}$, where these are shifts right 2 and right 3 respectively?
Sometimes we can create a Cayley graph of a set of automorphisms without even knowing what the sets $X$ or $S$ are. All we need to know is how many automorphisms are in $S$, and some relationships about the automorphisms. The next problem has you examine a few more Cayley graphs.
Problem 31 (Cayley Graphs From Relations)
In each scenario below, you should draw a Cayley graph.
- Suppose that $X$ is a set, and that $S$ contains a single automorphism $s$ of $X$. Suppose also that we know $s^6$ is the identity (so following the arrow colored $c_s$ 6 times will return us to where we started). Construct a Cayley graph of $\text{span}(S)$. Is there more than one right answer to this?
- Suppose that we know $S$ contains two elements $a$ and $b$. We also know that $a^2$ and $b^4$ are both the identity. In addition, we know that $a\circ b=b\circ a$, so if we start somewhere and follow the arrows colored $c_a$ and then $c_b$, then we should end up at the same place if we followed the arrows colored $c_b$ and then $c_a$. Construct a graph that satisfies these relationships. We'll use the notation $$\left<a,b\mid a^2=id, b^4=id, a\circ b=b\circ a\right>$$ to tell us that $S=\{a,b\}$ with the relations listed after the $\mid$.
- Generalize your result above to draw a Cayley graph if instead of $b^4=id$ we have $b^k=id$.
If $X$ is a set, and $S$ is a set of permutations of $X$, then we already know how to create the span of $S$. In general, the span of $S$ will include more permutations than what we started with. However, sometimes we won't be able to obtain any new permutations by spanning $S$. When this happens, we say that the set of permutations is closed (under function composition). Here's a formal defintion.
Definition (A Closed Set Of Permutations)
We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.
The next problem has you prove some relationships between a set of permutations $S$ and its span.
Problem 32 (Relationship Between S And Its Span)
Let $S$ be a set of permutations of $X$.
- Prove that $S\subseteq \text{span}(S)$. In other words, we know that $S$ is always contained in its span; the span might be larger.
- Prove that if $\text{span}(S)\subseteq S$, then $S$ is closed.
- If $T\subseteq S$, then show that $\text{span}(T)\subseteq\text{span}(S)$.
In linear algebra, we looked at collections of vectors, and then spanned them to obtain vector spaces. Every vector space was the span of a collection of vectors. Every vector in the vector space could be written as a linear combination of the vectors used to span the span. In addition, a vector space is closed under linear combinations. This means that span of a vector space is itself. We've defined the exact same structure, but now with permutations of $X$. The next problem asks you to show that the span of a set of permutations is closed.
Problem 24 (The Span Of A Set Of Permutations Is Closed)
Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.
[Hint: You might want to let $H=\text{span}(S)$. We then need to show that $H=\text{span}(H)$, or that $\text{span}(S) = \text{span}(H)$. From the previous problem we already know that $H\subseteq \text{span}(H)$. We just need to show that $\text{span}(H)\subseteq \text{span}(S)$. So we need to show if $\sigma\in \text{span}(H)$ (it's a permutation combination of elements in $H$), then we must have $\sigma\in \text{span}(S)$ (it's a permutation combination of elements in $S$). You'll probably find yourself writing something along the lines of $\sigma = \sigma_1^{k_1}\circ \sigma_2^{k_2}\circ \cdots \sigma_n^{k_n}$ where $\sigma_i\in H$ and then have to express each $\sigma_k$ in terms of something else. ]
Definition (Integer Linear Combination Of Integers)
Let $a_1, a_2, \ldots, a_k$ be $k$ integers.
- An integer linear combination of these integers is an expression of the form $$c_1a_1+c_2 a_2+ \cdots+c_k a_k$$ where each coefficient $c_i$ is an integer.
- The span of the set of integers $\{a_1, a_2, \ldots, a_k\}$ is the set of all possible integer linear combinations of these integers, namely $$\text{span}(\{a_1, a_2, \ldots, a_k\})=\text{span}(a_1, a_2, \ldots, a_k)=\{c_1a_1+c_2 a_2+ \cdots+c_k a_k\mid c_i\in \mathbb{Z} \text{ for }1\leq i\leq k\}.$$ For ease of notation, we'll often leave off the set notation when spanning a set of integers.
- If the set $S$ of integers is infinite, then we still define the span of $S$ to be the set of all integer linear combinations of integers in $S$. Hence we know $x\in S$ if and only if there exists a natural number $k$ such that $x=c_1a_1+c_2 a_2+ \cdots+c_k a_k$ where $a_i\in S$ and $c_i\in \mathbb{Z}$ for $1\leq i\leq k$.
- When there are only two integers, we'll often use $a$ and $b$ as the integers, and $s$ and $t$ as the coefficients. So the set of all integer linear combinations of $a$ and $b$ is $$\text{span}(a,b) = \{sa+tb\mid s,t\in\mathbb{Z}\}.$$
Problem 33 (Integer Linear Combination Practice)
Complete the following.
- Compute the span of $3$, i.e. make a list of the elements in this set. In general, what is the span of a single integer $a$? (We know it by a different name.)
- What is $\text{span}(4,6)$? List the elements. Find a single number $a$ so that $\text{span}(a)=\text{span}(4,6)$.
- What is $\text{span}(4,5)$?
- Let $S=\{a_1,a_2,\ldots,a_k\}$ be a set of integers. Show that if $c\in \text{span}(S)$, then so is every multiple of $c$.
We've seen a lot of relationships in class about modular arithmetic, inverses mod n, simple shift encryption schemes, and more. The next problem makes a connection between some of these. We'll connect it to even more next time.
Problem 34 (When Does An Integer Have A Modular Multiplicative Inverse)
Let $a$ and $n$ be integers, with $n>1$. Show that the following are equivalent.
- The integer $a$ has a multiplicative inverse mod $n$
- We have $1\in \text{span}(a,n)$. In other words, we can write 1 as a linear combination of $a$ and $n$.
- We have $\text{span}(a,n)=\mathbb{Z}$. Remember that $\text{span}(a,n) = \{sa+tn\mid s,t\in\mathbb{Z}\}.$
Remember, to show that three things are equivalent you must show that each implies the other. One way to do this is show that 1 implies 2, then show that 2 implies 3, and then show that 3 implies 1. Then each implies the other.
The two problems above, together with much of our work from the previous two weeks, leads us to one of the biggest theorems in number theory. We'll prove these next time.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Corollary (When Are Two Numbers Relatively Prime)
Two nonzero numbers $a$ and $b$ are relatively prime (i.e. their greatest common divisor is 1) if and only if there exists $s$ and $t$ such that $sa+tb=1$.
October 4
The first few problems we will work on are carry overs from Wednesday. Here they are:
Problem 28 (Computing Multiplicative Inverses For Small N)
To use modular arithmetic in matrix encryption, we must be able to find the modular multiplicative inverse of $a \mod n$. For each $n\leq 13$ and $a\in \mathbb{Z}_n$, we now compute the inverse of $a\mod n$ or explain why it does not have one.
- Why does $0\mod n$ never have an inverse?
- What is the multiplicative inverse of $1\mod n$?
- For $n=3$, what is the multiplicative inverse of $a=2$.
- For $n=4$, show that 2 does not have an inverse by computing $2\cdot 0$, $2\cdot 1$, $2\cdot 2$, and $2\cdot 3$ all modulo $4$. What is $3^{-1}\mod 4$?
- For each $n$ between 5 and 13, create a table that shows the inverse of each $a\in \mathbb{Z}_n$. List the elements of $\mathbb{Z}_n$ along the top row, and beneath each element list the multiplicative inverse, or cross off the number if there is no multiplicative inverse.
When you are done you should have a list of the elements of $U(n)$ for each $n$ up to 13, as well as the inverse of each element in $U(n)$. Do you see any patterns?
For $n=9$, you should obtain a table somewhat similar to the following table.
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $a^{-1}$ | x | 1 | 5 | x | 7 | 2 | x | 4 | 8 |
If $X$ is a set, and $S$ is a set of permutations of $X$, then we can create a Caley graph for the span of $S$. Here's a formal definition.
Definition (Cayley Graph Of A Span Of Permutations)
Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.
We've done this with several automorphism groups of graphs, as well as simple shift permutation groups.
Problem 30 (Cayley Graphs Of Two Automorphism Groups)
Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.

We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).
- For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
- For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.
If $X$ is a set, and $S$ is a set of permutations of $X$, then we already know how to create the span of $S$. In general, the span of $S$ will include more permutations than what we started with. However, sometimes we won't be able to obtain any new permutations by spanning $S$. When this happens, we say that the set of permutations is closed (under function composition). Here's a formal defintion.
Definition (A Closed Set Of Permutations)
We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.
The next problem has you prove some relationships between a set of permutations $S$ and its span.
Problem 32 (Relationship Between S And Its Span)
Let $S$ be a set of permutations of $X$.
- Prove that $S\subseteq \text{span}(S)$. In other words, we know that $S$ is always contained in its span; the span might be larger.
- Prove that if $\text{span}(S)\subseteq S$, then $S$ is closed.
- If $T\subseteq S$, then show that $\text{span}(T)\subseteq\text{span}(S)$.
To show that $S\subseteq \text{span}(S)$ we must show that if $\sigma\in S$, then we have $\sigma\in \text{span}(S)$. So let $\sigma\in S$. The definition of span is $$\text{span}(S)=\{\sigma_1^{n_1}\circ \sigma_2^{n_2}\circ \cdots \circ \sigma_k^{n_k}\mid k\in \mathbb{N}, \text{ with } \sigma_i\in S \text{ and } n_i\in \mathbb{Z} \text{ for } i\in \{1,2,\ldots,k\}\ \}.$$ We need to show that we can pick a $k$ and then some values of $\sigma_i\in S$ and $n_i\in \mathbb{Z}$ so that $$\sigma= \sigma_1^{n_1}\circ \sigma_2^{n_2}\circ \cdots \circ \sigma_k^{n_k}.$$ If we let $k=1$, and we let $\sigma_1=\sigma$ and we let $n_1=1$, then we have $$\sigma= \sigma^{1}.$$ This shows that we can write $\sigma$ as a permutation combination of permutations in $S$, and hence $\sigma\in \text{span}(S)$. Because we've show that if $\sigma\in S$, then we have $\sigma\in \text{span}(S)$, this means that $S\subseteq \text{span}(S)$.
In linear algebra, we looked at collections of vectors, and then spanned them to obtain vector spaces. Every vector space was the span of a collection of vectors. Every vector in the vector space could be written as a linear combination of the vectors used to span the span. In addition, a vector space is closed under linear combinations. This means that span of a vector space is itself. We've defined the exact same structure, but now with permutations of $X$. The next problem asks you to show that the span of a set of permutations is closed.
Problem 24 (The Span Of A Set Of Permutations Is Closed)
Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.
Hint: You might want to let $H=\text{span}(S)$. We then need to show that $H=\text{span}(H)$, or that $\text{span}(S) = \text{span}(H)$. From the previous problem we already know that $H\subseteq \text{span}(H)$. We just need to show that $\text{span}(H)\subseteq \text{span}(S)$. So we need to show if $\sigma\in \text{span}(H)$ (it's a permutation combination of elements in $H$ namely $$\sigma = \sigma_1^{n_1}\circ \sigma_2^{n_2}\circ \cdots \circ \sigma_k^{n_k}$$ where $k\in \mathbb{N}$ with $\sigma_i\in H$ and $n_i\in \mathbb{Z}$ for $i\in \{1,2,\ldots,k\}$), then we must have $\sigma\in \text{span}(S)$ (it's a permutation combination of elements in $S$). Can you explain why each $\sigma_i$ above can be written as a permutation combination of elements in $S$?
Definition (Integer Linear Combination Of Integers)
Let $a_1, a_2, \ldots, a_k$ be $k$ integers.
- An integer linear combination of these integers is an expression of the form $$c_1a_1+c_2 a_2+ \cdots+c_k a_k$$ where each coefficient $c_i$ is an integer.
- The span of the set of integers $\{a_1, a_2, \ldots, a_k\}$ is the set of all possible integer linear combinations of these integers, namely $$\text{span}(\{a_1, a_2, \ldots, a_k\})=\text{span}(a_1, a_2, \ldots, a_k)=\{c_1a_1+c_2 a_2+ \cdots+c_k a_k\mid c_i\in \mathbb{Z} \text{ for }1\leq i\leq k\}.$$ For ease of notation, we'll often leave off the set notation when spanning a set of integers.
- If the set $S$ of integers is infinite, then we still define the span of $S$ to be the set of all integer linear combinations of integers in $S$. Hence we know $x\in S$ if and only if there exists a natural number $k$ such that $x=c_1a_1+c_2 a_2+ \cdots+c_k a_k$ where $a_i\in S$ and $c_i\in \mathbb{Z}$ for $1\leq i\leq k$.
- When there are only two integers, we'll often use $a$ and $b$ as the integers, and $s$ and $t$ as the coefficients. So the set of all integer linear combinations of $a$ and $b$ is $$\text{span}(a,b) = \{sa+tb\mid s,t\in\mathbb{Z}\}.$$
Problem 33 (Integer Linear Combination Practice)
Complete the following.
- Compute the span of $3$, i.e. make a list of the elements in this set. In general, what is the span of a single integer $a$? (We know it by a different name.)
- What is $\text{span}(4,6)$? List the elements. Find a single number $a$ so that $\text{span}(a)=\text{span}(4,6)$.
- What is $\text{span}(4,5)$?
- Let $S=\{a_1,a_2,\ldots,a_k\}$ be a set of integers. Show that if $c\in \text{span}(S)$, then so is every multiple of $c$.
We've seen a lot of relationships in class about modular arithmetic, inverses mod n, simple shift encryption schemes, and more. The next problem makes a connection between some of these. We'll connect it to even more next time.
Problem 34 (When Does An Integer Have A Modular Multiplicative Inverse)
Let $a$ and $n$ be integers, with $n>1$. Show that the following are equivalent.
- The integer $a$ has a multiplicative inverse mod $n$
- We have $1\in \text{span}(a,n)$. In other words, we can write 1 as a linear combination of $a$ and $n$.
- We have $\text{span}(a,n)=\mathbb{Z}$. Remember that $\text{span}(a,n) = \{sa+tn\mid s,t\in\mathbb{Z}\}.$
Remember, to show that three things are equivalent you must show that each implies the other. One way to do this is show that 1 implies 2, then show that 2 implies 3, and then show that 3 implies 1. Then each implies the other.
We've seen two parts of this in class. The only part left is to show that (3) implies (1). So if $\text{span}(S)=\mathbb{Z}$, show that $a$ has a modular multiplicative inverse. We'll finish this up in small groups.
Problem 15(Division Algorithm Proof)
Prove the Division algorithm.
Problem 36 (Permutations of $U(n)$)
Suppose $n$ is an integer greater than 1 and let $X=U(n)$, so the set of integers mod $n$ that have a multiplicative inverse mod $n$. For each $a\in U(n)$, we can define a permutation of $U(n)$ by $f_a(x)=xa\pmod n$ for each $x\in U(n)$. This problem asks you to show that this is indeed a permutation of $U(n)$. This requires that you show the following:
- For each integer $n\geq 2$, show that if $a\in U(n)$ and $x\in U(n)$, then the product $f_a(x)=xa\pmod n\in U(n)$. This shows that $f_a:U(n)\to U(n)$ is a map from $U(n)$ to $U(n)$.
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is one-to-one. (As a reminder, one-to-one means that if $f_a(x)=f_a(y)$, then $x=y$.)
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is onto. (As a reminder, onto means that if $y\in U(n)$, then there exists $x\in U(n)$ such that $f_a(x)=y$.)
October 7
Problem 35 (Connecting Multiples And Spans Of Integers)
Suppose that $a$ and $b$ are integers.
- Prove that if $a$ is a multiple of $b$, then we must have $\text{span}(a)\subseteq\text{span}(b)$.
- Is the converse of the statement above true or false? Make sure you prove your result.
Problem (Inverting Function Composition)
Let $f:A\to B$, $g:B\to C$, and $h:C\to D$ be bijections.
- Show that the inverse of $g\circ f$ is $f^{-1}\circ g^{-1}$. See the note below if you forgot how to prove something is the inverse.
- What is the inverse of $h\circ g\circ f$? Remember to justify your claim.
Remember that you can show a function $k:B\to A$ is the inverse of $f:A\to B$ by showing that $f\circ k=id_B$ is the identity on $B$ and that $k\circ f=id_A$ is the identity on $A$. This means you must show that $f(k(b))=b$ for every $b\in B$, and that $k(f(a))=a$ for every $a\in A$.
This problem was on the list Friday, and I'll repeat it here now.
Problem 36 (Permutations of $U(n)$)
Suppose $n$ is an integer greater than 1 and let $X=U(n)$, so the set of integers mod $n$ that have a multiplicative inverse mod $n$. For each $a\in U(n)$, we can define a permutation of $U(n)$ by $f_a(x)=xa\pmod n$ for each $x\in U(n)$. This problem asks you to show that this is indeed a permutation of $U(n)$. This requires that you show the following:
- For each integer $n\geq 2$, show that if $a\in U(n)$ and $x\in U(n)$, then the product $f_a(x)=xa\pmod n\in U(n)$. This shows that $f_a:U(n)\to U(n)$ is a map from $U(n)$ to $U(n)$.
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is one-to-one. (As a reminder, one-to-one means that if $f_a(x)=f_a(y)$, then $x=y$.)
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is onto. (As a reminder, onto means that if $y\in U(n)$, then there exists $x\in U(n)$ such that $f_a(x)=y$.)
For part 2, you'll need to show that if $ax\pmod n=ay\pmod n$, then $x=y$. Here's a hint that should help you throughout the entire semester. Ask yourself, "How would I solve this if we were just working with the integers and we needed to show $ax=ay$ implies $x=y$?" Remove the word divide from your vocabulary, and replace it with "multiply by the inverse."
Problem 37 (Three Similar Cayley Graphs From Different Contexts)
This problem asks you to draw 3 Cayley graphs. Each Cayley graph should only have 4 vertices.
- Draw a Cayley graph for the set $H_4$ of simple shift permutations of $X=\{1,2,3,4\}$ using the generating set $S=\{\phi_1\}$.
- Then draw a Cayley graph for the span of the permutation $(1,4,3,2)$, which we wrote in disjoint cycle notation.
- Then draw a Cayley graph for $\{f_a\mid a\in U(5)\}$ using the generating set $S=\{f_2\}$. Remember that $f_a$ is a permutation of $U(5)$ defined by $f_a(x)=xa\pmod 5$.
- What do you notice about these Cayley graphs?
The three graphs from the previous problem look very similar, so much so that we could obtain one from the other if we just relabeled the vertex sets. This suggests that in some sense these graphs are the same. We now introduce a formal way to talk about when two graphs are the same.
Definition (Isomorphic Graphs)
Let $G$ and $H$ be two graphs, where we use $V(G)$ and $V(H)$ to denote the vertex sets. A function $f:V(G)\to V(H)$ is called an isomorphism of graphs $G$ and $H$ if $f$ is a bijection and $\{x,y\}$ is an edge of $G$ if and only if $\{f(x),f(y)\}$ is an edge of $H$ (see Wikipedia).
- We call this function $f$ an isomorphism because it "preserves the edge structure" in the graph. In general the word isomorphism refers to a bijection that preserves some kind of structure.
- If there exists an isomorphism of graphs between $G$ and $H$, then we say that $G$ and $H$ are isomorphic.
- If $G$ and $H$ are directed graphs, then an isomorphism of directed graphs would preserve the arrow structure.
- If the directed graphs $G$ and $H$ are colored, then an isomorphism also preserves the color structure, in the sense that $(a,b)$ and $(c,d)$ share the same color if and only if $(f(a),f(b))$ and $(f(c),f(d))$ share the same color.
Problem 38 (Introduction To Cayley Graph Isomorphisms)
Let $H_6 = \{\phi_0,\phi_1,\ldots,\phi_5\}$ be the set of simple shift permutations on an alphabet with 6 letters. Let $K=\{f_a\mid a\in U(7)\}$ be the set of permutations $f_a:U(7)\to U(7)$ defined by $f_a(x)=xa\pmod 7$. Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_1\}$. Then draw the Cayley graph of $K$ generated by $\{f_3\}$. Finally show that the function $g:H_6\to K$ defined by $$ g(\phi_0)=f_1, g(\phi_1)=f_3, g(\phi_2)=f_2, g(\phi_3)=f_6, g(\phi_4)=f_4, g(\phi_5)=f_5, $$ is an isomorphism of Cayley graphs.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_2, \phi_3\}$. Then draw the Cayley graph of $K$ generated by $\{f_2,f_6\}$. Do you believe these two Cayley graphs are isomorphic? You can just give a heuristic argument, rather than a formal proof.
- Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$. We've already shown this set has 6 permutations. Draw a Cayley graph of $S_3$ generated by the permutations $(1,2,3)$ and $(1,2)$. Do you think that this Cayley graph is isomorphic to any of the Cayley graphs above? Why?
We'll also be looking at the proofs to the two problems that we did not get to from last time. I'll repeat them here. Focus on the five problems above.
Problem 24 (The Span Of A Set Of Permutations Is Closed)
Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.
Problem 15(Division Algorithm Proof)
Prove the Division algorithm.
I will have some problems up for Wednesday before I head home today. If you want to work ahead some, please do.
October 9
Problem 35 (Connecting Multiples And Spans Of Integers)
Suppose that $a$ and $b$ are integers.
- Prove that if $a$ is a multiple of $b$, then we must have $\text{span}(a)\subseteq\text{span}(b)$.
- Is the converse of the statement above true or false? Make sure you prove your result.
We only need to show the last part of this. The first half was done in class. I'll have 4 different people finish this up in smaller groups.
Problem (Inverting Function Composition)
Let $f:A\to B$, $g:B\to C$, and $h:C\to D$ be bijections.
- Show that the inverse of $g\circ f$ is $f^{-1}\circ g^{-1}$. See the note below if you forgot how to prove something is the inverse.
- What is the inverse of $h\circ g\circ f$? Remember to justify your claim.
Remember that you can show a function $k:B\to A$ is the inverse of $f:A\to B$ by showing that $f\circ k=id_B$ is the identity on $B$ and that $k\circ f=id_A$ is the identity on $A$. This means you must show that $f(k(b))=b$ for every $b\in B$, and that $k(f(a))=a$ for every $a\in A$.
Problem 36 (Permutations of $U(n)$)
Suppose $n$ is an integer greater than 1 and let $X=U(n)$, so the set of integers mod $n$ that have a multiplicative inverse mod $n$. For each $a\in U(n)$, we can define a permutation of $U(n)$ by $f_a(x)=xa\pmod n$ for each $x\in U(n)$. This problem asks you to show that this is indeed a permutation of $U(n)$. This requires that you show the following:
- For each integer $n\geq 2$, show that if $a\in U(n)$ and $x\in U(n)$, then the product $f_a(x)=xa\pmod n\in U(n)$. This shows that $f_a:U(n)\to U(n)$ is a map from $U(n)$ to $U(n)$.
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is one-to-one. (As a reminder, one-to-one means that if $f_a(x)=f_a(y)$, then $x=y$.)
- Given $n\geq 2$ and $a\in U(n)$, show that $f_a$ is onto. (As a reminder, onto means that if $y\in U(n)$, then there exists $x\in U(n)$ such that $f_a(x)=y$.)
For part 2, you'll need to show that if $ax\pmod n=ay\pmod n$, then $x=y$. Here's a hint that should help you throughout the entire semester. Ask yourself, "How would I solve this if we were just working with the integers and we needed to show $ax=ay$ implies $x=y$?" Remove the word divide from your vocabulary, and replace it with "multiply by the inverse."
The three graphs from the previous problem look very similar, so much so that we could obtain one from the other if we just relabeled the vertex sets. This suggests that in some sense these graphs are the same. We now introduce a formal way to talk about when two graphs are the same.
Definition (Isomorphic Graphs)
Let $G$ and $H$ be two graphs, where we use $V(G)$ and $V(H)$ to denote the vertex sets. A function $f:V(G)\to V(H)$ is called an isomorphism of graphs $G$ and $H$ if $f$ is a bijection and $\{x,y\}$ is an edge of $G$ if and only if $\{f(x),f(y)\}$ is an edge of $H$ (see Wikipedia).
- We call this function $f$ an isomorphism because it "preserves the edge structure" in the graph. In general the word isomorphism refers to a bijection that preserves some kind of structure.
- If there exists an isomorphism of graphs between $G$ and $H$, then we say that $G$ and $H$ are isomorphic.
- If $G$ and $H$ are directed graphs, then an isomorphism of directed graphs would preserve the arrow structure.
- If the directed graphs $G$ and $H$ are colored, then an isomorphism also preserves the color structure, in the sense that $(a,b)$ and $(c,d)$ share the same color if and only if $(f(a),f(b))$ and $(f(c),f(d))$ share the same color.
Problem 38 (Introduction To Cayley Graph Isomorphisms)
Let $H_6 = \{\phi_0,\phi_1,\ldots,\phi_5\}$ be the set of simple shift permutations on an alphabet with 6 letters. Let $K=\{f_a\mid a\in U(7)\}$ be the set of permutations $f_a:U(7)\to U(7)$ defined by $f_a(x)=xa\pmod 7$. Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_1\}$. Then draw the Cayley graph of $K$ generated by $\{f_3\}$. Finally show that the function $g:H_6\to K$ defined by $$ g(\phi_0)=f_1, g(\phi_1)=f_3, g(\phi_2)=f_2, g(\phi_3)=f_6, g(\phi_4)=f_4, g(\phi_5)=f_5, $$ is an isomorphism of Cayley graphs.
- Draw the Cayley graph of $H_6$ generated by $\{\phi_2, \phi_3\}$. Then draw the Cayley graph of $K$ generated by $\{f_2,f_6\}$. Do you believe these two Cayley graphs are isomorphic? You can just give a heuristic argument, rather than a formal proof.
- Let $S_3$ be the set of all permutations on $X=\{1,2,3\}$. We've already shown this set has 6 permutations. Draw a Cayley graph of $S_3$ generated by the permutations $(1,2,3)$ and $(1,2)$. Do you think that this Cayley graph is isomorphic to any of the Cayley graphs above? Why?
Just as we defined a set of permutations to be closed under composition combinations of permutations, we can define a set of integers to be closed under integer linear combinations of integers. We'll say that a nonempty set $S$ of integers is closed (under integer linear combinations) if the span of the set $S$ equals the original set $S$, so again we have $S=\text{span}(S)$. The proof of the following fact should be very similar to one you have already shown.
Problem 39 (The Span Of A Set Of Integers Is Closed)
Let $S$ be a nonempty set of integers. Prove that $\text{span}(S)$ is closed under integer linear combinations.
Problem 39.5 (Function Composition Is Associative)
Let $f:A\to B$, $g:B\to C$, and $h:C\to D$ be functions. Recall that $g\circ f:A\to C$ is a new function defined by $(g\circ f)(x) = g(f(x))$, i.e. first put $x$ into $f$ to obtain $f(x)$ and then put $f(x)$ into $g$ to obtain $g(f(x))$.
Prove that function composition is associative, i.e. show that $h\circ (g\circ f)=(h\circ g)\circ f$.
Remember, to show that two functions $p:X\to Y$ and $q:V\to W$ are equal, you must show that they (1) have the same domains $X=V$, (2) they have the same codomains $Y=W$, and (3) that $p(x)=q(x)$ for each $x\in X$.
Click to see a solution.
First note that $h\circ (g\circ f)$ and $(h\circ g)\circ f$ have the same domain $A$ and codomain $D$. All we must show now is that $(h\circ (g\circ f))(x)=((h\circ g)\circ f)(x)$ for every $x\in A$. Let $x\in A$. We then compute $$(h\circ (g\circ f))(x) = h((g\circ f)(x)) = h(g(f(x))).$$ We can also compute $$((h\circ g)\circ f)(x) = (h\circ g)(f(x)) = h(g(f(x))).$$ This proves that $(h\circ (g\circ f))(x)=((h\circ g)\circ f)(x)$, as desired.
Problem 40 (Properties Of Closed Sets Of Permutations)
Let $H$ be a nonempty closed set of permutations of a set $X$.
- Show that the identity function $id_X$ is in $H$.
- Show that if $\sigma\in H$, then so is $\sigma^{-1}$.
- Show that if $\alpha\in H$ and $\beta\in H$, then $\alpha\circ \beta\in H$.
- Show that if $\alpha,\beta,\gamma\in H$, then $\alpha\circ (\beta\circ \gamma) = (\alpha\circ \beta)\circ \gamma$.
There are several problems already up for Friday. I'll try to always have a few problems up ahead of time.
October 11
We've talked about automorphisms of graphs and directed graphs. We can similarly define automorphisms of colored directed graphs.
Definition (Automorphism Of A Colored Directed Graph)
Let $\mathcal{G}=(V,C,A)$ be a colored directed graph, where the vertex set is $V$ and the list of colored arrows is $A$, where each arrow in the list $A$ is assigned a unique color from $C$. An automorphism of a directed colored graph is a permutation $\sigma:V\to V$ of the vertex set such that $(x,y)$ is an arrow colored $c\in C$ if and only if $(\sigma(x),\sigma(y))$ is an arrow colored $c$. In other words, it's a permutation of $H$ that preserves the arrow and color structure of the graph.
A Cayley graph is a colored directed graph. We've drawn many Cayley graphs and noticed that they are highly symmetric. Every point has the same number of arrows leaving (and entering). Any pattern we see at one vertex appears at every other vertex. If you were to stand at any vertex and look outwards, the graph would appear the same from every point. This next problem has you show this. You'll show that if $s$ is one of the permutations used to create arrows, then the map $f_s:H\to H$ defined by $f_s(\sigma)=\sigma\circ s$ is an automorphism of the Cayley graph. Once you've shown that the graph looks the same by following one arrow, you can repeatedly apply this process to show that the graph looks the same by following any sequence of arrows.
Problem 41 (Translating By An Arrow In A Cayley Graph Is An Automorphism)
Let $X$ be a set and let $S$ be a set of permutations of $X$. Let $H=\text{span}(S)$ and let $\mathcal{G}$ be the Cayley graph $(H,S)$, so we know $(x,y)$ is an arrow colored $c_t$ where $t\in S$ if and only if $y=t \circ x$. Pick an element $s\in S$ (one of the elements used to create arrows). Prove that the function $f_s:H\to H$ defined by $f_s(\sigma)=\sigma\circ s$ is an automorphism of the Cayley graph. You must show the following three things:
- The function $f_s$ is a permutation. (State the inverse and show it is the inverse.)
- If $(x,y)$ is an arrow colored $c_t$, then $(f_s(x),f_s(y))$ is an arrow colored $c_t$. In other words, if $t\circ x=y$, then explain why $t\circ f_s(x) = f_s(y)$.
- If $(f_s(x),f_s(y))$ is an arrow colored $c_t$, then $(x,y)$ is an arrow colored $c_t$.
Problem (Closed Under Function Composition)
Suppose that $H$ is a set of permutations of $X$. Suppose also that if $\alpha,\beta\in H$, then we must have $\alpha\circ \beta\in H$. Use induction to prove that for every $n\in \mathbb{N}$, if we know $\sigma_1,\sigma_2,\ldots,\sigma_n\in H$, then we must have $$\sigma_1\circ\sigma_2\circ\cdots\circ\sigma_n\in H.$$
In the previous problem we assumed that if if $\alpha,\beta\in H$, then we must have $\alpha\circ \beta\in H$. Any time a set $H$ of permutations satisfies this, we say that the set $H$ is closed under composition. Similarly we say that set is closed under taking inverse if $\alpha\in H$ implies $\alpha^{-1}\in H$. We've been saying that a set of permutations is closed (under composition combinations of permutation) when the set contains any composition combination of permutations of the set. This next problems shows a simpler way to prove that a set is closed, and it requires showing only that the set is closed under composition and closed under taking inverses.
Problem (Characterizing Closed Sets Of Permutations)
Let $H$ be a set of permutations of a set $X$. Suppose that $H$ satisifies the following 4 properties.
- The identity function $id_X$ is in $H$.
- If $\sigma\in H$, then so is $\sigma^{-1}$.
- If $\alpha\in H$ and $\beta\in H$, then so is $\alpha\circ \beta\in H$.
- If $\alpha,\beta,\gamma\in H$, then we have $\alpha\circ (\beta\circ \gamma) = (\alpha\circ \beta)\circ \gamma$.
Prove that $H$ is closed.
Definition (Binary Operation)
Let $G$ be a set. A binary operation on $G$ is a way of combining two elements of $G$ to obtain a new element in $G$. Formally, we just say that a binary operation $*$ is function $*:G\times G\to G$, and we use the notation $a*b$ to represent the function notation $*(a,b)$.
You've been using binary operations your whole life.
Problem 39 (Binary Operation Introduction)
In which of the following scenarios do we have a binary operation on a set $G$. Justify your answers.
- Addition $a+b$ of integers.
- Multiplication $A\cdot B$ of 3 by 3 matrices.
- The dot product $\vec u\cdot \vec v$ of two dimensional vectors.
- The cross product $\vec u\times \vec v$ of three dimensional vectors.
- The scalar product $c\cdot \vec v$.
- Composition $f\circ g$ of permutations on the same set $X$.
- Composition $f\circ g$ of functions from $X$ to $Y$.
Up to this point in the semester, we've been focusing solely on sets of permutations. Every element was a function, which often required keeping track of a bunch of information that wasn't necessary. Spanning a set of permutations gave us closed sets of permutations. We found that there are 4 key properties of a set of closed permutations. Let's now drop the requirement that we have permutations, and instead focus on sets, together with a binary operation, that satisfy these 4 properties. We call a set with these properties a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
We've already seen many groups throughout the semester. In the problem Characterizing Closed Sets Of Permutations, we showed that any closed set of permutations is a group. Since the span of any set of permutations is closed, then every time we span a set of permutations, we end up with a group. All of the patterns you have discovered about simple shift permutations, automorphisms of graphs, and more, we will be able to transfer to your understanding of abstract groups. Let's look an example, namely a group of matrices that we used before to encrypt messages.
Problem 40 (General Linear Group Introduction)
We've used matrices mod $5$ to encrypt a simple message. The set of possible 2 by 2 matrices mod $5$ that we can use as an encryption key is an important set in cryptography. It's called a general linear group and written $\text{GL}(2,\mathbb{Z}_5)$. We can generalize this to $m$ by $m$ matrices mod $n$ and write $\text{GL}(m,\mathbb{Z}_n)$, though generally we require that $n$ be a prime. With each of the problems below, a single sentence or two is enough to answer the question.
- If we want $A$ to serve as a valid matrix for encryption, what must we require about $A$? One sentence is fine.
- If $A\in \text{GL}(2,\mathbb{Z}_5)$, show that $A^{-1}\in \text{GL}(2,\mathbb{Z}_5)$.
- If $A\in \text{GL}(2,\mathbb{Z}_5)$ and $B\in \text{GL}(2,\mathbb{Z}_5)$, why is $AB\in \text{GL}(2,\mathbb{Z}_5)$?
- Prove that if we know for some integer $k$ that $A_1,A_2,A_3,\ldots,A_k \in \text{GL}(2,\mathbb{Z}_5)$, then we know $A_1A_2A_3\cdots A_k\in \text{GL}(2,\mathbb{Z}_5)$.
- Is $\text{GL}(2,\mathbb{Z}_5)$ a group? (Which of the group properties did we not show above? Are they true?)
- Do your arguments above hold when considering $\text{GL}(m,\mathbb{Z}_n)$ for every $m,n \in \mathbb{N}$ such that $n\geq 2$? A conjecture with a reasonable justification (not a complete a proof) is fine in this part.
In the definition of a group, it said that there exists an element $e\in G$ such that $ex=xe=e$ for each $x\in G$. It refers to this element as the identity. Could there be two such elements? Similarly, could an element have two inverses? The next problem has you show that the identity and inverses are unique.
Problem 41 (The Identity And Inverses Are Unique)
Suppose that $(G,\cdot)$ is a group.
- Prove that the identity of the group is unique.
- Prove that if $x\in G$, then the inverse of $x$ is unique.
You then need to show why $e_1=e_2$. Your second proof is similar.
Problem 42 (The GCD Theorem Proof)
Prove the GCD Theorem.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Hint: If you intersect $\text{span}(a,b)$ with the natural numbers, then you can apply the well ordering principle to get the smallest positive element $d$ of this intersection. You then just have to show that this smallest positive element $d$ is the greatest common divisor. This requires that you show
- that $d$ is a common divisor, and
- that $d$ is the greatest common divisor.
To show that $d$ divides both $a$ and $b$, use the division algorithm to obtain $a=qd+r$, and explain why the remainder must be zero. Then you must show that if $c$ is any other common divisor, then $d$ is greater, so $d\geq c$.
October 14
Problem (Write up an induction proof)
Please make sure you write up a final draft induction proof for the problem Closed Under Function Composition. Use complete sentences, just as you would on the wiki. You are welcome to type it up on the wiki (in which case you can use copy/paste to get the LaTeX code). Make sure you bring a copy to class (hand written or typed), and hand it in. I want to read your proofs and help you each improve. Make sure that whatever words you use are your own. DO NOT LOOK at someone else's proof, as then I won't be able to give you feedback about your writing.
Click to show the problem.
Problem (Closed Under Function Composition)
Suppose that $H$ is a set of permutations of $X$. Suppose also that if $\alpha,\beta\in H$, then we must have $\alpha\circ \beta\in H$. Use induction to prove that for every $n\in \mathbb{N}$, if we know $\sigma_1,\sigma_2,\ldots,\sigma_n\in H$, then we must have $$\sigma_1\circ\sigma_2\circ\cdots\circ\sigma_n\in H.$$
This does not replace your week 4 write up, so you'll need to pick a different problem and write it up by Wednesday.
Problem (Review two problems from last time)
We did not have time in class to review the solutions to the following problems:
- Characterizing Closed Sets Of Permutations
- The Identity And Inverses Are Unique - You'll find solutions to this in chapter 2 of your text.
A ton of you had these, so if you did, please move on. If you did not yet get these, please spend some time with them before proceeding. If you are unable to get them, then assume they are true and keep working on the problem set.
Click to show these problems.
Problem (Characterizing Closed Sets Of Permutations)
Let $H$ be a set of permutations of a set $X$. Suppose that $H$ satisifies the following 4 properties.
- The identity function $id_X$ is in $H$.
- If $\sigma\in H$, then so is $\sigma^{-1}$.
- If $\alpha\in H$ and $\beta\in H$, then so is $\alpha\circ \beta\in H$.
- If $\alpha,\beta,\gamma\in H$, then we have $\alpha\circ (\beta\circ \gamma) = (\alpha\circ \beta)\circ \gamma$.
Prove that $H$ is closed.
Problem 41 (The Identity And Inverses Are Unique)
Suppose that $(G,\cdot)$ is a group.
- Prove that the identity of the group is unique.
- Prove that if $x\in G$, then the inverse of $x$ is unique.
Let's start today by analyzing a new type of encryption that we have not yet introduced. We've spent quite a bit of time looking at modular multiplicative inverses and the sets $\mathbb{Z}_n$ and $U(n)$. Let's take a minute and explore an encryption problem that uses these sets.
Definition (Affine Encryption Key)
Suppose we have an alphabet with $n$ letters. Set up a 1-1 correspondence between the letters in your alphabet and the integers 0 to $n-1$. As an example, we could let $n=27$ for the standard alphabet with 26 letters and a space (the 27th letter which we'll number 0), and then use the correspondence in the table below.
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
Pick an integer $m\geq n$. Then an affine encryption key is an invertible function \( f:\mathbb{Z}_m \to \mathbb{Z}_m\) defined by $$f(x)=ax+b\pmod {m}$$ for some $a,b\in\mathbb{Z}_m$.
Problem 43 (Affine Encryption Key Introduction)
If we let $m=31$, then we can use the function $f(x)=5x+12\pmod m$ to encrypt the message "save them" by (1) swapping the letters to the numbers (19,1,22,5,0,20,8,5,13) and then (2) applying $f(x)$ to each letter to obtain the encrypted numbers (14, 17, 29, 6, 12, 19, 21, 6, 15).
- Find $c,d\in \mathbb{Z}_{31}$ so that the inverse of $f$ is $f^{-1}(x)=cx+d$ where $c,d\in \mathbb{Z}_{31}$.
- If instead we let $m=27$, then find the inverses of $f(x)=2x+17\pmod{27}$ or explain why it cannot be done.
- Give an example of nonzero $a,b\in \mathbb{Z}_{27}$ so that $f(x)=ax+b\pmod{27}$ is not invertible.
You've been studying groups since you started adding integers back in grade school. Just about every idea we've encountered since the start of the semester has also been a group. Now that we have isolated the key properties that make up a group, we need to become comfortable with showing that sets with a binary operation are groups, i.e. we need to become comfortable with checking the four properties of closure, associativity, identity, and inverses.
Let's practice showing that some sets are groups by showing that $\mathbb{Z}_n$ and $U(n)$ are groups. If we already showed a key fact in a previous problem, feel free to refer to problem by name and state the fact that was proved there. We have already shown most of the reasons why the sets below are groups.
Problem 44 ($\mathbb{Z}_n$ and $U(n)$ are groups)
Show the following. You need to briefly explain why the set together with its binary operation satisfies the definition of a group.
- For each $n\geq 1$, the set $\mathbb{Z}_n$ is a group under addition mod $n$.
- For each $n\geq 2$, prove that $U(n)$ is a group under multiplication mod $n$.
Try to solve the problems above without looking up the definition of a group.
If you need to, click here to show the definition of a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
Because of how we defined groups, anytime we span a collection of permutations of a set $X$ we should get a group. The next problem has you show this. Each question can be answered by referring to things we have already shown. Feel free to look at the pages September and October for a list of all the problems we have solved each day. If you have not yet printed the work we are doing, I would suggest that you print a copy for reference as you work on new problems.
Problem 45 (Spans Of Permutations Are Subgroups)
Let $X=\{1,2,3,\ldots,n\}$. Let $S_n$ be the set of all permutations of $X$ (so we know there are $n!$ such permutations).
- Show that $S_n$ is a group under function composition $\circ$.
- If $H$ is a subset of $S_n$ that is closed (under composition combinations of permutations), prove that $H$ is a group under function composition.
- Let $S$ be a nonempty subset of $S_n$. Show that $\text{span}(S)$ is a group under function composition.
In the previous problem, we saw if $S\subseteq S_n$ then $\text{span}(S)$ is a not only just a subset of the group $S_n$, but is itself a group. The operation we use in the smaller group $(\text{span}(S),\circ)$ comes from the operation we used in the larger group $(S_n,\circ)$. Because of this close connection, we call $\text{span}(S)$ a subgroup of $S_n$ and write $\text{span}(S)\leq S_n$. Let's now make a formal definition.
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
In the proof of problem Characterizing Closed Sets Of Permutations, we did not need to use the first and fourth properties listed to show that the set of permutations $H$ was closed. The next problem replicates this, but now in terms of subgroups instead of in terms of closed sets of permutations.
Problem 46 (The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses)
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- If $a,b\in H$, then $ab\in H$. (We say $H$ is closed under the group operation.)
- If $a\in H$, then $a^{-1}\in H$. (We say $H$ is closed under taking inverses.)
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
October 16
The following problem again asks you to make sure you are comfortable with the definitions of a binary operation and a group. Thanks to Justin for coming by my office and asking some questions that led to the creation of this problem. Thanks to all of you for your consistent daily effort. I'm really enjoying being your teacher. Keep up the great work.
Problem 47 (Can We Use Division To Create A Group)
Let $G=\mathbb{R}$ and $H=\mathbb{R}\setminus \{0\}$.
- Show that division $a\div b$ is not a binary operationon $G$.
Definition (Binary Operation)
Let $G$ be a set. A binary operation on $G$ is a way of combining two elements of $G$ to obtain a new element in $G$. Formally, we just say that a binary operation $*$ is function $*:G\times G\to G$, and we use the notation $a*b$ to represent the function notation $*(a,b)$.
- Show that division $a\div b$ is a binary operation on $H$.
- Since division is a binary operation on $H$, determine if $(H,\div)$ is a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- Does $e=1$ satisfy the property of being an identity?
- If $x\in H$, find an inverse $x^{-1}\in H$ or explain why none exists.
- Is the operation $\div$ associative?
Just as we spanned sets of permutations, we can span subsets of a group. After defining this, we'll show that spanning a subset of a group always gets you a subgroup of the group. This should be analogous to the fact that spanning a subset of permutations leads to a closed set of permutations.
Definition (The Subgroup Generated By A Subset)
Let $G$ be a group. Suppose that $S$ is a subset of $G$.
- A word from the alphabet $S$ is a product of the form $$x=s_1s_2\cdots s_k$$ where for each $i$ either $s_i\in S$ or $s_i^{-1}\in S$.
- The subgroup generated by $S$ is the set of words from the alphabet $S$, namely $$\left<S\right> = \{s_1s_2\cdots s_k\mid k\in \mathbb{N} \text{ and either $s_i\in S$ or $s_i^{-1}\in S$ for each } i\in\{1,2,\ldots, k\}\}.$$
- If $H=\left<S\right>$, then we say that $H$ is the subgroup generated by $S$, or that $S$ is a generating set for $H$.
- If $S=\{a\}$, then we'll write $\left<a\right>$ instead of $\left<\{a\}\right>$. We call $\left<a\right>$ the subgroup generated by $a$.
We call $\left<S\right>$ the subgroup of $G$ generated by $S$, but we have not yet shown this is in fact a subgroup. The next problem has you verify this, so that we can definitely refer to $\langle S\rangle$ as a subgroup.
Problem 51 (The Subgroup Generated By S Is Actually A Subgroup)
Let $G$ be a group and $S$ be a nonempty subset of $G$. Prove that $\left<S\right>$ is a subgroup of $G$.
Definition ($|a|$ and $|G|$ - Order For Elements and Groups)
Let $G$ be a group with identity $e$, and let $g\in G$.
- The $\textdef{order}$ of $G$, denoted $|G|$, is the cardinality of $G$.
- The $\textdef{order}$ of $g$, denoted $|g|$, is the smallest positive integer $n$ such that $g^n = e$, if such an $n$ exists. If no such $n$ exists, we say $g$ has infinite order.
Definition (The Euler Phi Function)
The Euler phi function $\varphi:\mathbb{Z}\to\mathbb{Z}$ is defined by letting $\varphi(n)$ equal the order of $U(n)$.
Problem 48 (Orders Of $\mathbb{Z}_n$ And $U(n)$ And Their Elements)
We've already shown that $\mathbb{Z}_n$ under addition mod $n$ and $U(n)$ under multiplication mod $n$ are groups.
- For each $n$ between 2 and 10, compute the order of $Z_n$ and the order of each element of $\mathbb{Z}_n$. Organize your work into a table where you first make a list of the elements, and then underneath each element state the order. For example, if $n=6$ then our table would look like the one below. $$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Element}&0&1&2&3&4&5\\\hline \text{Order}&1&6&3&2&3&6\\\hline \end{array}$$
- For each $n$ between 2 and 10, compute the order of $U(n)$ (state $\varphi(n)$) and then compute the order of each element of $U(n)$. You can check your work with the sage code below. I kept the numbers under 10 because you can do these by hand (or in your head) fairly quickly. Make sure you do enough by hand that you feel comfortable with this process.
- You should have noticed that $U(8)$ and $U(10)$ both have order 4. Is there a 1-1 correspondence between these two groups that matches elements with the same order?
Here's some Sage code you can use to check your computations with $U(n)$.
for n in (2..20):
Zn = Integers(n)
Un = [x for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
show(table(["U("+str(n)+r") has order $\varphi($"+str(n)+"$)=$"+str(len(Un))+
".The elements, with orders below them, are listed below."]))
orders=[x.multiplicative_order() for x in Un] #This computes the multiplicative order of each element.
show(table([Un,orders])) #This creates a table of elements (top row) and their orders (bottom row).
Definition (Group Isomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{isomorphism}$ if $f$ is a bijection and $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$. We say that $G$ and $H$ are isomorphic groups, and write $G\approx H$ if there exists an isomorphism between them.
When two groups are isomorphic, they must have the same order because the function $f$ is a bijection. However, not only do two isomorphic groups need to have the same cardinality, but in addition the bijection creates a correspondence between elements of the same order. Each group must have the same number of elements of each order, and any isomorphism must map an element of order $k$ to an element of order $k$. The next problem has you prove this.
Problem 68 (The Orders Of Elements Match In Isomorphic Groups)
Suppose that $f:G\to H$ a group isomorphism. Suppose that $f(g)=h$. Prove that the order of $g$ and the order of $h$ are the same, in other words show that $|g|=|h|$. In particular, since the only elements of order 1 in each group are the identities $e_G\in G$ and $e_H\in H$, then we must have $f(e_G)=e_H$.
Click here to see a partial proof that's missing one piece.
Suppose that $f:G\to H$ is an isomorphism and that $e_G$ and $e_H$ are the identities in $G$ and $H$ respectively. We first show that $f(e_G)=e_H$. Note that $e_Ge_G=e_G$. Apply $f$ to both sides to obtain $f(e_G)f(e_G)=f(e_G)$. Since $f(e_G)=f(e_G)e_H$, we now have $f(e_G)f(e_G)=f(e_G)\cdot e_H.$ Cancelling $f(e_G)$ from the left of both sides gives $f(e_G)=e_H$ as desired.
We now prove that if $a$ has order $n$, then $f(a)$ must have order $n$ as well. Suppose $a\in G$ has order $n$. This means that $n$ is the smallest positive integer such that $a^n=e_G$, or that $aa \cdots a=e$ (repeated $n$ times). If we apply $f$ to both sides of this equation, then we see that $f(a)f(a)\cdots f(a)=f(e_G)$. This means that $f(a)^n=f(e_G)$. Since we know $f(e_G)=e_H$, then we have shown $f(a)^n=e_H$ is the identity. This means the order of $f(a)$ must equal $n$. $\square$
What's missing? Pay close attention to the definition of order.
Click here to see a partial proof that's missing one piece.
Suppose that $f:G\to H$ is an isomorphism and that $e_G$ and $e_H$ are the identities in $G$ and $H$ respectively. Suppose $a\in G$ has order $n$. This means that $n$ is the smallest positive integer such that $a^n=e_G$, or that $aa \cdots a=e$ (repeated $n$ times). If we apply $f$ to both sides of this equation, then we see that $f(a)f(a)\cdots f(a)=f(e_G)$. This means that $f(a)^n=f(e_G)$. If we knew that $f(e_G)=e_H$, then this means that the order of $f(g)$ must equal $n$ because then $f(g)^n=e_H$ is the identity.
We now show that $f(e_G)=e_H$. First note that $e_Ge_G=e_G$. Apply $f$ to both sides to obtain $f(e_G)f(e_G)=f(e_G)$. Since $f(e_G)=f(e_G)e_H$, we now have $f(e_G)f(e_G)=f(e_G)\cdot e_H.$ Cancelling $f(e_G)$ from the left of both sides (in other words multiplying by the inverse of $f(e_G)$ and simplifying) gives $f(e_G)=e_H$ as desired. $\square$
What's missing? Pay close attention to the definition of order.
We used Cayley graphs to give us a visual representation of the span of a set of permutations. Similarly, we can use Cayley graphs to help us visualize groups. The definition is very similar.
Definition (Cayley Graph Of A Group)
Let $G$ be a group that is generated by a set $S$. The Cayley graph of $G$ generated by $S$, which we'll write as $(G,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $G$. Each vertex corresponds to an element of the group.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $g$, we draw the colored arrow $(g ,s g)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(g,g)$ at each vertex.
If the Cayley graphs of two groups are isomorphic, we would expect the groups to be isomorphic as well. We'll prove this eventually, but for now let's just use this fact to start sorting out isomorphic groups. The next problem has you look at 60+ Cayley graphs and visually start sorting groups.
Problem (Cayley Graphs and Isomorphisms between $\mathbb{Z}_n$ and $U(m)$)
In this problem, we will construct Cayley graphs of $\mathbb{Z}_n$ and $U(n)$ for many values of $n$. Our goal is to build a table of groups, where each row of the table consists of isomorphic groups.
- Start by drawing the Cayley graphs of $\mathbb{Z}_2$, $\mathbb{Z}_3$, $\mathbb{Z}_4$, and $\mathbb{Z}_5$ using $x=1$ as the generator. What pattern do you notice?
- If you wanted to draw the Cayley graph of $\mathbb{Z}_{50}$ using $x=1$ as the generator, what would your graph look like?
- If $\mathbb{Z}_n\cong\mathbb{Z}_m$, what do you know about $n$ and $m$?
- The two blocks of sage code below will draw Cayley graphs of $U(n)$ for each $n$ from 2 to 60. Evaluate each block of code now.
for n in (2..30): Zn = Integers(n) Un = [x for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un show(table(["U("+str(n)+") has order "+str(len(Un))+ ".The elements, with orders below them, are listed below."])) orders=[x.multiplicative_order() for x in Un] #This computes the multiplicative order of each element. show(table([Un,orders])) #This creates a table of elements (top row) and their orders (bottom row). Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un S=Zn.unit_gens() CG=DiGraph([Un,lambda i,j:False]) for k in S: CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k]) for u,v,l in CGk.edges(): CGk.set_edge_label(u,v,k) CG.add_edges(CGk.edge_iterator()) CG.graphplot(color_by_label=True,edge_labels=True).show()for n in (31..60): Zn = Integers(n) Un = [x for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un show(table(["U("+str(n)+") has order "+str(len(Un))+ ".The elements, with orders below them, are listed below."])) orders=[x.multiplicative_order() for x in Un] #This computes the multiplicative order of each element. show(table([Un,orders])) #This creates a table of elements (top row) and their orders (bottom row). Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un S=Zn.unit_gens() CG=DiGraph([Un,lambda i,j:False]) for k in S: CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k]) for u,v,l in CGk.edges(): CGk.set_edge_label(u,v,k) CG.add_edges(CGk.edge_iterator()) CG.graphplot(color_by_label=True,edge_labels=True).show() - For each $n$ between 2 and 60, use a Cayley graph to determine if $U(n)$ is isomorphic to $U(m)$ for some $m<n$. Place your results in a table. If $U(n)$ is not isomorphic to any previous group on your table, put it in the left column of the table as a new row. Otherwise, place $U(n)$ to the right of the corresponding $U(m)$ to which it is isomorphic. If $U(n)$ has a single generator, add the appropriate $\mathbb{Z}_m$ to your table as well. Each row in your table should consists of isomorphic groups, and groups on different rows should not be isomorphic to each other. I've already done up through $U(12)$ in the table below, but I suggest you start at $U(2)$ and check that the table below is correct. $$\begin{array}{|c|c|}
\hline
\text{Group}&\text{Isomorphic Groups}\\ \hline
U(2)&\mathbb{Z}_1, \\
U(3)&\mathbb{Z}_2, U(4), U(6),\\
U(5)&\mathbb{Z}_4, U(10), \\
U(7)&\mathbb{Z}_6, U(9), \\
U(8)&U(12)\\
U(11)&\mathbb{Z}_{10} \\
\vdots&\vdots\\
\end{array}
$$
- When you encounter a graph that is not generated by a single element, compare it to previous graphs that you've already seen. How could you make the new graph by combining previous graphs? For example, the graph of $U(8)$ looks like a bunch of graphs of $\mathbb{Z}_2$. The graph of $U(15)$ looks like two copies of $\mathbb{Z}_4$ connected with $\mathbb{Z}_2$'s. The first 5 new graphs (not generated by a single element) that you should encounter after $U(12)$ are at 15, 21, 24, 32, and 33.
We've made tons of conjectures about patterns we've seen in $Z_n$ and $U(n)$. It's time to prove them and start using them as facts, instead of conjectures. For example, we've already noticed that something has a multiplicative modular inverse mod $n$ if and only if it is relative prime to $n$. In problem .... (click to expand), we showed that .... The following problem provides the key tool to proving most of the conjectures we've made. While you'll find the proof to this in chapter 0 of the text, please try doing it without reading the proof. We'll use this theorem to prove most of our conjectures on Friday.
Problem 42 (The GCD Theorem Proof)
Prove the GCD Theorem.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Hint: If you intersect $\text{span}(a,b)$ with the natural numbers, then you can apply the well ordering principle to get the smallest positive element $d$ of this intersection. You then just have to show that this smallest positive element $d$ is the greatest common divisor. This requires that you show
- that $d$ is a common divisor, and
- that $d$ is the greatest common divisor.
To show that $d$ divides both $a$ and $b$, use the division algorithm to obtain $a=qd+r$, and explain why the remainder must be zero. Then you must show that if $c$ is any other common divisor, then $d$ is greater, so $d\geq c$.
The definition of $\langle S\rangle$ above is very similar to our definition of span that we used earlier. It's missing the exponents that we had in our definition of the span. The next problem has you show that including the powers or not gives us the same thing.
Problem 66 (The Subgroup Generated By S Equals The Span Of S)
Let $G$ be a group. Suppose that $S$ is a subset of $G$. To parallel our definition of the span of a set of permutations, we could have defined the span of $S$ to be $$\text{span}(S)= \{t_1^{n_1}t_2^{n_2}\cdots t_j^{n_j}\mid j\in \mathbb{N} \text{ and $t_i\in S$ with $n_i\in \mathbb{Z}$ for each } i\in\{1,2,\ldots, j\}\}.$$ Instead we defined the subgroup generated by $\langle S \rangle$ to be $$\left<S\right> = \{s_1s_2\cdots s_k\mid k\in \mathbb{N} \text{ and either $s_i\in S$ or $s_i^{-1}\in S$ for each } i\in\{1,2,\ldots, k\}\}.$$ Using the definitions above, prove that these two sets are the same, so prove $\text{span}(S)=\left<S\right>$. In other words, prove that the subgroup generated by $S$ and the span of $S$ are precisely one and the same.
October 18
For Friday, the problems below are to help you practice with the group axioms. Spend 15 minutes on each problem. Make sure you are ready to come to class to present a few of each, and hopefully all. Each problem has a fairly short answer.
In class, we'll split up into small groups and take turns presenting. If you have not presented in class very much, you need to make sure you are ready to present Friday.
Click to see the definitions of a group and subgroup, as well as the subgroup test.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
Problem 46 (The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses)
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- If $a,b\in H$, then $ab\in H$. (We say $H$ is closed under the group operation.)
- If $a\in H$, then $a^{-1}\in H$. (We say $H$ is closed under taking inverses.)
Definition (Subgroup)
Let $(G,\cdot)$ be a group, and let $H$ be a nonempty subset of $G$. Then $H$ is called a $\textdef{subgroup}$ of $G$ if the following hold:
- $\textbf{[Closure]}$ for all $h,k\in H$ we have $h\cdot k\in H$, and
- $(H,\cdot)$ is a group.
When $H$ is a subgroup of $G$, we write $H\le G$. Any subgroup of $G$ that is not equal to $G$ itself we call a $\textdef{proper subgroup}$. The subset of $G$ consisting of just the identity we call the $\textdef{trivial subgroup}$.
Problem 49 (Cancellation Laws For Groups)
Suppose $G$ is a group. Let $a,b,c\in G$. Prove that if $ca=cb$, then $a=b$. A similar proof will show that if $ac=bc$, then $a=b$.
Problem 50 (The Inverse In A Finite Group Is A Power Of The Element)
Let $G$ be finite group with $a\in G$. Prove that there exists a positive integer $k$ such that $a^k=a^{-1}$.
Problem 51 (Inverses In Groups)
Suppose that $G$ is a group with $a,b\in G$.
- Prove that the inverse of $a^{-1}$ is $a$.
- Prove that the inverse of $ab$ is $b^{-1}a^{-1}$.
- If $a_1,a_2,a_3,\ldots, a_n\in G$, state the inverse of $a_1a_2a_3\cdots a_n$. Use induction to prove your claim.
Problem 52 (Heisenberg Matrix Group)
Let $G$ be the set of all 3 by 3 matrices with entries in the real numbers of the form $$\begin{bmatrix}1&a&b\\0&1&c\\0&0&1\end{bmatrix}.$$ Prove that $G$ is group under matrix multiplication. This group is often called the Heisenberg group and is connected to the Heisenberg uncertainty principle. See page 51 in your text for an interesting historical fact.
Problem 53 (Finite Subgroup Test)
Let $G$ be a group. Suppose that $H$ is a nonempty finite subset of $G$ and that $H$ is closed under the operation of $G$ (so if $a,b\in H$, then we must have $ab\in H$). Prove that $H$ is a subgroup of $G$.
Problem 54 (The Intersection Of Two Subgroups)
Suppose that $G$ is a group and that $H$ and $K$ are subgroups of $G$. Prove that $H\cap K$ is a subgroup of $G$.
Problem 55 (The Union Of Two Subgroups)
Suppose that $G$ is a group and that $H$ and $K$ are subgroups of $G$. Is $H\cup K$ a subgroup of $G$? Either prove that is, or find a counterexample.
Definition (Abelian Group)
Let $G$ be a group. If $ab=ba$ for every $a,b\in G$ (so the group operation is commutative), then we say that $G$ is Abelian.
Definition ($Z(G)$ - Center Of A Group)
Let $G$ be a group. The center of the group, written $Z(G)$, is the set of elements $x\in G$ that commute with every element of $G$, which we can write symbolically as $$Z(G)=\{x\in G\mid gx=xg \text{ for all } g\in G\}.$$
Problem 56 (The Center Of Group Is A Subgroup)
Prove that the center $Z(G)$ of a group $G$ is a subgroup of $G$. If $G$ is Abelian, then what is $Z(G)$?
Problem 57 (Powers Of Products In An Abelian Group)
Suppose $G$ is an Abelian group. Prove that if $a,b\in G$, then $(ab)^2=a^2b^2$. Then use induction to prove that if $a,b\in G$, then $(ab)^n=a^nb^n$ for each $n\in \mathbb{N}$.
October 21
Problem (Problems from the past)
We already have people ready to present these problems. If you have not yet completed them, please spend 10 minutes tops with each. Don't let yourself get bogged down with completing each of these before class, but make sure that you at least have spent 10 minutes with each (otherwise the discussion in class is pointless).
Click to see the problems.
Problem 47 (Can We Use Division To Create A Group)
Let $G=\mathbb{R}$ and $H=\mathbb{R}\setminus \{0\}$.
- Show that division $a\div b$ is not a binary operationon $G$.
Definition (Binary Operation)
Let $G$ be a set. A binary operation on $G$ is a way of combining two elements of $G$ to obtain a new element in $G$. Formally, we just say that a binary operation $*$ is function $*:G\times G\to G$, and we use the notation $a*b$ to represent the function notation $*(a,b)$.
- Show that division $a\div b$ is a binary operation on $H$.
- Since division is a binary operation on $H$, determine if $(H,\div)$ is a group.
Definition (Group)
Let $G$ be a nonempty set, and let $*$ be a binary operation on $G$, which means for every $x,y\in G$ we have $x*y\in G$ $\textbf{[Closure]}$. The structure $\mathbb{G} = (G,*)$ is called a $\textdef{group}$ if the following hold.
- $\textbf{[Associativity]}$ For all $x,y,z\in G$ we have $(x* y)* z = x* (y* z)$.
- $\textbf{[Identity]}$ There is an $e\in G$ such that for all $x\in G$ we have $x * e = e* x = x$.
- $\textbf{[Inverses]}$ For all $x\in G$ there is a $y\in G$ such that $x* y = y* x = e$.
We usually simply write $G$ when referring to the entire structure $\mathbb{G}=(G,*)$. The element $e$ from the second point is called the $\textdef{identity}$. The element $y$ from the third point is called the $\textdef{inverse}$ of $x$ and is usually denoted $x^{-1}$. One often simply writes $xy$ in place of $x*y$, and for every positive integer $n$, we'll write $x^n$ as shorthand for $x* x* \cdots * x$ ($n$ times).
- Does $e=1$ satisfy the property of being an identity?
- If $x\in H$, find an inverse $x^{-1}\in H$ or explain why none exists.
- Is the operation $\div$ associative?
Problem 48 (Orders Of $\mathbb{Z}_n$ And $U(n)$ And Their Elements)
We've already shown that $\mathbb{Z}_n$ under addition mod $n$ and $U(n)$ under multiplication mod $n$ are groups.
- For each $n$ between 2 and 10, compute the order of $Z_n$ and the order of each element of $\mathbb{Z}_n$. Organize your work into a table where you first make a list of the elements, and then underneath each element state the order. For example, if $n=6$ then our table would look like the one below. $$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Element}&0&1&2&3&4&5\\\hline \text{Order}&1&6&3&2&3&6\\\hline \end{array}$$
- For each $n$ between 2 and 10, compute the order of $U(n)$ (state $\varphi(n)$) and then compute the order of each element of $U(n)$. You can check your work with the sage code below. I kept the numbers under 10 because you can do these by hand (or in your head) fairly quickly. Make sure you do enough by hand that you feel comfortable with this process.
- You should have noticed that $U(8)$ and $U(10)$ both have order 4. Is there a 1-1 correspondence between these two groups that matches elements with the same order?
Here's some Sage code you can use to check your computations with $U(n)$.
for n in (2..20):
Zn = Integers(n)
Un = [x for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
show(table(["U("+str(n)+r") has order $\varphi($"+str(n)+"$)=$"+str(len(Un))+
".The elements, with orders below them, are listed below."]))
orders=[x.multiplicative_order() for x in Un] #This computes the multiplicative order of each element.
show(table([Un,orders])) #This creates a table of elements (top row) and their orders (bottom row).
Problem 42 (The GCD Theorem Proof)
Prove the GCD Theorem.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Hint: If you intersect $\text{span}(a,b)$ with the natural numbers, then you can apply the well ordering principle to get the smallest positive element $d$ of this intersection. You then just have to show that this smallest positive element $d$ is the greatest common divisor. This requires that you show
- that $d$ is a common divisor, and
- that $d$ is the greatest common divisor.
To show that $d$ divides both $a$ and $b$, use the division algorithm to obtain $a=qd+r$, and explain why the remainder must be zero. Then you must show that if $c$ is any other common divisor, then $d$ is greater, so $d\geq c$.
Problem 56 (The Center Of Group Is A Subgroup)
Prove that the center $Z(G)$ of a group $G$ is a subgroup of $G$. If $G$ is Abelian, then what is $Z(G)$?
Problem 57 (Powers Of Products In An Abelian Group)
Suppose $G$ is an Abelian group. Prove that if $a,b\in G$, then $(ab)^2=a^2b^2$. Then use induction to prove that if $a,b\in G$, then $(ab)^n=a^nb^n$ for each $n\in \mathbb{N}$.
Problem 9(Simple Shift Repetition)
Let's now devise a way to not only encrypt a message, but also keep track of who has seen the message? There are several ways to do this. Let's look at an example that involves repeated application of the same encrpytion key. For this example, let's use the encryption key $\phi_4:S\to S$ (the simple shift permutation that shifts right 4).
A group of military commanders decide to send messages using a message chain. The message passes sequentially from one person to the next, where at each stage they apply the encryption key to the ciphertext before sending it on. If I want to send the plain text message $attackatdawn$, then I'd send the message $exxegoexhear$ to the person after me in the chain. This person would decipher the text using $\phi_4^{-1}$ (shift left 4), and then apply $\phi_4$ to the cipher text $exxegoexhear$ and then send the ciphertext $ibbiksibliev$ to the person after them in the chain. This would repeat until the message made it to every commander.
- You receive the cipher text $skkzgzkomnz$. What is the plain text message? How many people have seen this message?
- How many commanders can we include in this encryption scheme and still tell who sent the message?
- If we use $\phi_5$ instead of $\phi_4$, how many commanders can we include in this encryption scheme and still tell who sent the message?
- Is there an encryption key $\phi_n$ so that $\phi_n^2=\phi_0$. In other words, is there an encryption key $\phi_n$ that will only allow up to two commands to be in the chain?
Definition (Subgroup Generated By An Element)
Let $G$ be a group and $a\in G$. Then the subgroup generated by $a$ is the set $$\langle a\rangle = \{a^n\mid n\in\mathbb{Z}\},$$ where we define $a^0=e$ and $a^{-n}=(a^{-1})^n$.
Problem 58 (The Subgroup Generated By An Element Is Actually A Subgroup)
Let $G$ be a group with $a\in G$. Show that $\langle a\rangle$, using the definition above, is a subgroup of $G$.
Problem 59 (The Intersection Of Two Subgroups Of $\mathbb{Z}$)
Let $G=\mathbb{Z}$. Because the group operation is addition, remember that $a^2$ actually means $a+a$, and $a^5=a+a+a+a+a=5a$. Beware of this issue, as $a^n$ actually means $na$ because the group operation is addition when working in $\mathbb{Z}$.
- What is $\langle 2\rangle$? What is $\langle 3\rangle$? Convince yourself that $\langle 2\rangle\cap \langle 3\rangle = \langle 6\rangle$.
- What is $\langle 4\rangle$? What is $\langle 6\rangle$? Find an integer $c$ so that $\langle c\rangle=\langle 4\rangle\cap \langle 6\rangle$? Prove that your result is true.
- If $a,b\in \mathbb{Z}$, then conjecture what $c$ should equal so that $\langle c\rangle=\langle a\rangle\cap \langle b\rangle$. You don't have to prove this result (unless you'd rather prove this result than proving part 2).
Definition (The Subgroup $n\mathbb{Z}$)
For each $n\in \mathbb{N}$ we define $n\mathbb{Z}$ to be the subgroup $\langle n\rangle = \{kn\mid k\in \mathbb{Z}\}$ of the group $\mathbb{Z}$ under addition. This is just the multiples of $n$.
When we were working with simple shift permutations of the standard 26 letter alphabet, we showed that the set of all simple shift permutations, which we denoted $H=\{\phi_n\mid n\in\mathbb{Z}\}$, was actually a set that consisted of just 26 elements, namely we showed that $H=\{\phi_0,\phi_1, \ldots,\phi_{25}\}$. Each of these simple shifts can be generated using $\phi_1$, and the order of $\phi_1$ is $|\phi_1|=26$. Using the language of groups, we showed that $$H =\langle \phi_1\rangle = \{\phi_0,\phi_1, \ldots,\phi_{25}\}.$$ We showed this was true because if $n\in \mathbb{Z}$, then we could use the division algorithm to write $n=26q+r$ where $0\leq r<26$. Then we knew that $$\phi_1^{n}=\phi_1^{26q+r}=\phi_1^{26q}\circ \phi_1^r = \phi_0\circ \phi_r = \phi_r.$$ We knew that any repeated shift of 26 letters would take us back to the identity. We now generalize this problem to show that if an element of a group has order $n$, then $\langle a\rangle$ must always consist of the elements $\{e,a,a^2,\ldots, a^{n-1}\}$.
Problem 60 (Properties Of $\langle a \rangle$ When $a$ Has Finite Order)
Let $G$ be a group with $a\in G$. Suppose that the order of $a$ is $|a|=n$. Prove the following:
- We have $\langle a\rangle = \{e,a,a^2,\ldots, a^{n-1}\}$. (You are showing two sets are equal.)
- We have $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
- The order of an element equals the order of the subgroup generated by that element, namely $|a|=|\langle a\rangle|$. (How can you combine 1 and 2 to get this.)
Exercise (If $a^k=e$, Then The Order Of $a$ Divides $k$)
Suppose that $a$ is a group element with order $n$. If $a^k=e$, prove that $k$ is a multiple of $n$.
Click to see a solution.
Suppose $a^k=e$. This means $a^k=a^0$, which from the previous problem is true if and only if $k-0$ is a multiple of $n$. This shows that $k=k-0$ is a multiple of $n$.
Exercise (Properties Of An Element With Infinite Order)
Let $G$ be a group with $a\in G$. Suppose that the order of $a$ is infinite. Show that $a^i=a^j$ if and only if $i=j$, and state the order of $\langle a\rangle$.
Click to see a solution.
Suppose the order of $a$ is infinite. Then by definition this means that $a^n\neq e$ unless $n=0$. Clearly if $i=j$ then $a^i=a^j$. We only need to prove the converse of this statement. Suppose that $a^i=a^j$, and assume without loss of generality that $i\geq j$. Then $a^{i-j}=e$ (just multiply both sides on the right by $a^{-j}$). Because $a$ has infinite order, then we know $a^k\neq e$ for any positive integer $k$. Since $i-j\geq 0$ and $a^{i-j}=e$, we must have $i-j=0$. This means $i=j$.
The next problem asks you to compute the center $Z(G)$ of a nonabelian group, and the result is not trivial group. The automorphisms of the square gave us a group with 8 elements. This group consisted of 4 rotations and 4 reflections. Similarly, for any regular $n$-gon we can construct the automorphism group which will have order $2n$ and consist of $n$ rotations and $n$ reflections.
Definition (The Dihedral Groups $D_{n}$)
For each integer $n\geq 2$, we define the dihedral group on $n$ vertices, written $D_{n}$, to be automorphism group of the regular $n$-gon. This group consists of $n$ rotations and $n$ reflections, so has order $2n$.
Problem 61 (The Center Of A Dihedral Group)
Let $G=D_4$, the automorphism group of the square. Recall that $Z(G)$ is the center of the group, or the set of elements that commute with every element of the group.
- What is $\langle R_{90} \rangle$? What is $\langle R_{180} \rangle$? What is $\langle R_{270} \rangle$? What is $\langle H \rangle$?
- Does $R_{90}\in Z(G)$? Explain. (Does $R_{90}$ commute with every element in $G$? In particular, does $R_{90}H=HR_{90}$?)
- Compute the center $Z(G)$ and show that it consists of more than just $R_0$. Make sure you can explain why each element is either in $Z(G)$, or not in $Z(G)$.
October 23
Every time you seen an Exercise in the problem set, you should spend a couple minutes trying to answer the question. These questions are designed as a quick check of some facts that you should be familiar with. Come up with a solution, and then click to see the solution.
Exercise (What Is The Group Operation On The Integers)
If we want to consider $\mathbb{Z}$ as group, then which operation do we use, addition or multiplication? Why? Which is a group, is it $(\mathbb{Z},+)$ or is it $(\mathbb{Z},\cdot)$?
Click to see a solution.
The integers are a group under addition (the sum of two integers is an integer, the identity is 0, the inverse of $n$ is $-n$, and addition is associative as an axiom). For multiplication, the inverse of $2$, which is $1/2$, is not an integer so $\mathbb{Z}$ is not closed under inverses. There is no multiplicative inverse of 0 as $0x\neq 1$ for any integer $x$.
Exercise (Are The Natural Numbers A Subgroup Of The Integers)
Is $\mathbb{N}$ closed under the operation of addition? Is $\mathbb{N}$ a subgroup of $\mathbb{Z}$?
Click to see a solution.
The sum of two positive integers is a positive integer, so $\mathbb{N}$ is closed under the operation of $\mathbb{Z}$ (which is addition). However, the inverse of $2$ under addition is $-2$, but $-2\notin \mathbb{N}$. This shows that $\mathbb{N}$ is not closed under taking inverses, and hence is not a group (so not a subgroup of $\mathbb{Z}$).
We'll start today by showing that if $H$ is a nonempty finite subset of a group that is closed under the operation, then it automatically is a subgroup. You should find that your work from the problem The Inverse In A Finite Group Is A Power Of The Element should help. Remember, the key was to consider the sequence $a, a^2, a^3, a^4, \ldots$ which cannot consist of all different elements, which means there must be $i,j\in \mathbb{Z}$ with $a^i=a^j$ and $j>i$. Try repeating the argument almost exactly, but this time pay attention to what happens if $j-i-1=0$.
Problem 53 (Finite Subgroup Test)
Let $G$ be a group. Suppose that $H$ is a nonempty finite subset of $G$ and that $H$ is closed under the operation of $G$ (so if $a,b\in H$, then we must have $ab\in H$). Prove that $H$ is a subgroup of $G$.
Take a moment to reread the problem The Span Of A Simple Shift. In this problem, we looked at the span of various simple shift permutations. We saw many patterns that we conjectured without proof. In particular, we noticed that two simple shifts $\phi_i$ and $\phi_j$ had the same span if they had the same greatest common divisor with 12 (the size of the alphabet). It's time to prove this conjecture, as well as many more.
The following problem requires that you use the GCD theorem. If you let $d=\gcd(n,k)$, then remember that there are integers $s$ and $t$ such that $d=sn+tk$. This will be your key tool in working with the greatest common divisor.
Problem 62 ($\langle a^k\rangle = \langle a^{\gcd(k,|a|)}\rangle$)
Let $a$ be an element of order $n$ and let $k\in\mathbb{N}$. Prove that $\langle a^k\rangle = \langle a^{\gcd(k,n)}\rangle$.
You'll need to use the definition of order, and two previos problems to make short work of this problem. In particular, if you pay attention to the fact that the order of an element always matches the order of the subgroup generated by that element, then you can make sense of $|a^k|$ in terms of a greatest common divisor.
Problem 63 ($|a^k| = |a|/\gcd(k,|a|)$)
Let $a$ be an element of order $n$.
- If $d$ is a divisor of $n$, then prove that $|a^d|=n/d$.
- For any $k\in \mathbb{N}$, prove that $|a^k| = n/\gcd(k,n)$.
The previous two problems are the key tools to unlocking all of our other conjectures about simple shift permutations. In particular, the order of a simple shift permutation on $n$ letters will always be a divisor of $n$. Let's first make a new definition, a cyclic group, to generalize any group that behaves like the simple shift permutations.
Definition (Cyclic Group)
Let $G$ be a group. If there exists an element $a\in G$ such that $\langle a\rangle=G$, then we say that $G$ is a cyclic group.
Problem 64 ($\langle a^i \rangle = \langle a^j \rangle$ iff $\gcd(i,n)=\gcd(j,n)$)
Let $G$ be a group. Suppose that $a\in G$ has order $n>1$. Prove the following two facts:
- If $G$ is a cyclic group, then the order of $a$ divides the order of the group.
- We have $\langle a^i \rangle = \langle a^j \rangle$ if and only if $\gcd(i,n)=\gcd(j,n)$.
Click for a hint.
- If $G$ is cyclic, then pick a generator, say $b$. This means $G=\langle b\rangle$. Why does this mean $a=b^k$ for some $k$? Use this to show that $b$ has finite order, say $m$. Then use problem 63 with $b^k$, where $|b|=m$, rather than $a^k$ and $|a|=n$.
- Problem 63 will get you one direction, and problems 62 will get you the other.
The second fact proves the following three corollaries by letting $i=1$.
- We have $\langle a \rangle = \langle a^j \rangle$ if and only if $\gcd(n,j)=1$.
- A simple shift permutation $\phi_j$ on $n$ letters generates all simple shift permutations on $n$ letters if and only if $\gcd(n,j)=1$.
- An integer $j\in \mathbb{Z}_n$ is a generator of $\mathbb{Z}_n$ if and only if $\gcd(n,j)=1$.
What does this have to do with the problem When Does An Integer Have A Modular Multiplicative Inverse? You should see a connection between this problem and elements of $U(n)$.
Exercise (Cyclic Groups Are Abelian)
Suppose that $G$ is a cyclic group. Prove that $G$ is an Abelian group.
Click to see a solution.
Since $G$ is cyclic, we know that there exists some $a\in G$ with $\langle a\rangle = G$. Let $x,y\in G$. We need to show that $xy=yx$. But we know that $x=a^m$ and $y=a^n$ for some $n,m\in \mathbb{Z}$ because $G$ is cyclic. This means that $$xy=a^ma^n=a^{m+n}=a^{n+m}=a^na^m=yx,$$ which is what we needed to show.
October 25
In class, someone asked if it was enough to just show that something worked as an inverse on one side. In linear algebra, you showed this was true for matrices, namely that if you knew $BA=I$, then you also know that $AB=I$. This fact is also true in groups.
Problem.One Sided Inverses Are Sufficient
Let $G$ be a group and let $x,y\in G$. Prove that if $yx=e$, then $y$ is the inverse of $x$. In other words, if you can show that $y$ is a one-sided inverse of $x$, then it must be a two-sided inverse.
We need to review the definition of the order of a group.
Definition ($|a|$ and $|G|$ - Order For Elements and Groups)
Let $G$ be a group with identity $e$, and let $g\in G$.
- The $\textdef{order}$ of $G$, denoted $|G|$, is the cardinality of $G$.
- The $\textdef{order}$ of $g$, denoted $|g|$, is the smallest positive integer $n$ such that $g^n = e$, if such an $n$ exists. If no such $n$ exists, we say $g$ has infinite order.
If you feel like you need extra practice with this definition, then please complete the following exercise.
Exercise.Practice with Order
In each part below, you are given an element $a$ of a group $G$. Find the order of that element.
- Let $a= R_{270}$ which is an element of $D_{8}$, the automorphisms of a square.
- Let $a= R_{30}$ which is a 30 degree rotation and an element of $D_{48}$, the automorphisms of a regular 24-gon.
- Let $a=\left<\begin{bmatrix}2&1\\1&0\end{bmatrix}\right>$ in the general linear group $GL(2,\mathbb{Z}_3)$. [Hint: Just as all the previous problems, start computing powers of this matrix until you obtain the identity.]
- Let $a=(1,2,3,4,5)$ which is an element of the set of all permutations of $X=\{1,2,3,4,5\}$.
- Let $a=3$ as an element of $U(7)$.
- Let $a=2$ as an element of $U(17)$.
- Let $a=3$ as an element of $U(17)$.
Click to see a solution.
In each instance, we just have to compute $a^k$ for $k=1,2,3,\ldots$ until $a^k=e$. The smallest $k$ for which this occurs is the order of $a$. You should have obtained the answers 4, 12, 8, 5, 6, 8, 16. Make sure you can explain why for each.
Exercise.
Suppose we know that $a^6=e$.
- Explain why this is not enough information to state the order of $a$. (Look at the definition. What are we missing?)
- In addition to knowing that $a^6=e$, someone else notices that $a^4=e$. Prove that the order of $a$ cannot be 4. In particular show that $a^2=e$, so the order of $a$ is either $2$ or $1$.
Click to see a solution.
- The order of an element is the SMALLEST positive integers $n$ such that $a^n=e$. If all we know is that $a^6=e$, then the order might be 6, or some number less.
- If we know that both $a^6=e$ and $a^4=e$, then since $6=4+2$ (the division algorithm), we know that $e=a^6=a^{4+2}=a^4a^2=ea^2=a^2$. This shows that $e=a^2$, which means the order now can at most be 2.
Problem (The last half of what Kinsey shared in class - THIS IS A KEY PROBLEM)
Suppose that $a$ is an element of order $n$. Prove that $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
Problems from the past
We still have the following problems left that we need to present in class.
- Monday's, The Center Of A Dihedral Group
- All four problems from Wed. I'll be reassigning presenters for these, based on your preparation logs. Please report your progress on all 7 problems for today.
Please rework on these problems.
Click to view these problems, as well as some hints.
Problem 61 (The Center Of A Dihedral Group)
Let $G=D_4$, the automorphism group of the square. Recall that $Z(G)$ is the center of the group, or the set of elements that commute with every element of the group.
- What is $\langle R_{90} \rangle$? What is $\langle R_{180} \rangle$? What is $\langle R_{270} \rangle$? What is $\langle H \rangle$?
- Does $R_{90}\in Z(G)$? Explain. (Does $R_{90}$ commute with every element in $G$? In particular, does $R_{90}H=HR_{90}$?)
- Compute the center $Z(G)$ and show that it consists of more than just $R_0$. Make sure you can explain why each element is either in $Z(G)$, or not in $Z(G)$.
Here's a faster way. If you rotate clockwise $x$ degrees and then flip, that's the same as first flipping and then rotating $x$ degrees counterclockwise. The only way you could end up with a rotation and a flip commuting is if a counter clockwise rotation of $x$ degrees and a clockwise rotation of $x$ degrees resulted in the same action. You can also read the solution in chapter 3 of your text on page 63.
Problem 53 (Finite Subgroup Test)
Let $G$ be a group. Suppose that $H$ is a nonempty finite subset of $G$ and that $H$ is closed under the operation of $G$ (so if $a,b\in H$, then we must have $ab\in H$). Prove that $H$ is a subgroup of $G$.
Problem 62 ($\langle a^k\rangle = \langle a^{\gcd(k,|a|)}\rangle$)
Let $a$ be an element of order $n$ and let $k\in\mathbb{N}$. Prove that $\langle a^k\rangle = \langle a^{\gcd(k,n)}\rangle$.
Problem 63 ($|a^k| = |a|/\gcd(k,|a|)$)
Let $a$ be an element of order $n$.
- If $d$ is a divisor of $n$, then prove that $|a^d|=n/d$.
- For any $k\in \mathbb{N}$, prove that $|a^k| = n/\gcd(k,n)$.
Problem 64 ($\langle a^i \rangle = \langle a^j \rangle$ iff $\gcd(i,n)=\gcd(j,n)$)
Let $G$ be a group. Suppose that $a\in G$ has order $n>1$. Prove the following two facts:
- If $G$ is a cyclic group, then the order of $a$ divides the order of the group.
- We have $\langle a^i \rangle = \langle a^j \rangle$ if and only if $\gcd(i,n)=\gcd(j,n)$.
Click for a hint.
- If $G$ is cyclic, then pick a generator, say $b$. This means $G=\langle b\rangle$. Why does this mean $a=b^k$ for some $k$? Use this to show that $b$ has finite order, say $m$. Then use problem 63 with $b^k$, where $|b|=m$, rather than $a^k$ and $|a|=n$.
- Problem 63 will get you one direction, and problems 62 will get you the other.
The second fact proves the following three corollaries by letting $i=1$.
- We have $\langle a \rangle = \langle a^j \rangle$ if and only if $\gcd(n,j)=1$.
- A simple shift permutation $\phi_j$ on $n$ letters generates all simple shift permutations on $n$ letters if and only if $\gcd(n,j)=1$.
- An integer $j\in \mathbb{Z}_n$ is a generator of $\mathbb{Z}_n$ if and only if $\gcd(n,j)=1$.
What does this have to do with the problem When Does An Integer Have A Modular Multiplicative Inverse? You should see a connection between this problem and elements of $U(n)$.
October 28
Problem. The order an element equals the order of the subgroup generated by that element
If $a$ is a group element with order $n$, then we've shown the following two facts:
- $\langle a\rangle = \{e,a,a^2,\ldots, a^{n-1}\}$.
- $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
Use these two facts to prove that order of an element equals the order of the subgroup generated by that element, i.e. prove that $|a|=|\langle a\rangle|$.
We know that the following facts are true if $a$ is an element or order $n$.
- $\langle a\rangle = \{e,a,a^2,\ldots, a^{n-1}\}$.
- $a^i=a^j$ if and only if $i-j$ is a multiple of $n$.
- $|a|=|\langle a\rangle|$.
- $\langle a^k\rangle = \langle a^{\gcd(k,n)}\rangle$.
- If $d$ is a divisor of $n$, then $|a^d|=n/d$.
- For any $k\in \mathbb{N}$, we have $|a^k| = n/\gcd(k,n)$.
Use these facts to prove the last problem from Friday.
Problem 64 ($\langle a^i \rangle = \langle a^j \rangle$ iff $\gcd(i,n)=\gcd(j,n)$)
Let $G$ be a group. Suppose that $a\in G$ has order $n>1$. Prove the following two facts:
- If $G$ is a cyclic group, then the order of $a$ divides the order of the group.
- We have $\langle a^i \rangle = \langle a^j \rangle$ if and only if $\gcd(i,n)=\gcd(j,n)$.
Click for a hint.
- If $G$ is cyclic, then pick a generator, say $b$. This means $G=\langle b\rangle$. Why does this mean $a=b^k$ for some $k$? Use this to show that $b$ has finite order, say $m$. Then use problem 63 with $b^k$, where $|b|=m$, rather than $a^k$ and $|a|=n$.
- Problem 63 will get you one direction, and problems 62 will get you the other.
The second fact proves the following three corollaries by letting $i=1$.
- We have $\langle a \rangle = \langle a^j \rangle$ if and only if $\gcd(n,j)=1$.
- A simple shift permutation $\phi_j$ on $n$ letters generates all simple shift permutations on $n$ letters if and only if $\gcd(n,j)=1$.
- An integer $j\in \mathbb{Z}_n$ is a generator of $\mathbb{Z}_n$ if and only if $\gcd(n,j)=1$.
What does this have to do with the problem When Does An Integer Have A Modular Multiplicative Inverse? You should see a connection between this problem and elements of $U(n)$.
We've spent a lot of time working with cyclic groups and cyclic subgroups generated by a single element. The Well ordering principle and the GCD theorem have shown up quite a bit in our work. Let's now show that any time we start with a cyclic group, then every subgroup must also be cyclic. We've already seen this fact when we consider the problem Simple Shift Repetition where we used repeated shifting to send encrypted message to several generals.
Problem 65 (Subgroups Of Cyclic Groups Are Cyclic)
Suppose that $G$ is a cyclic group generated by $a$. Suppose that $H$ is a subgroup of $G$. Prove that there exists $k\in\mathbb{Z}$ such that $H = \left<a^k\right>$. In other words, prove that $H$ is itself a cyclic group.
Click to see a hint.
How can you get the smallest positive integer $k$ such that $a^k\in H$?
We've seen several times in class that when we compute $\text{span}(a,b)$ for integers $a$ and $b$, then their span equals $\text{span}(d)$ for a single integer $d$. In particular, we've also seen that this integer $c$ is precisely $d=\gcd(a,b)$. What if instead we wanted to look at the span of $k$ integers $\{a_1,a_2,a_3,\ldots, a_k\}$. Is there a single number $d$ that has the same span? The previous problem says that YES there must be a single number that achieves this. We call this the greatest common divisor of $a_1,a_2,a_3,\ldots, a_k$. The next exercise emphasizes this.
Exercise (The Subgroups Of $\mathbb{Z}$ are $n\mathbb{Z}$)
We know that $n\mathbb{Z}$ is a subgroup of $\mathbb{Z}$ for every integer $n$. Show that these are the only subgroups of $\mathbb{Z}$. In particular this means that the span of $k$ integers, which is a subgroup of $\mathbb{Z}$, must be equal to $d\mathbb{Z}$ for some $d\in \mathbb{Z}$.
Click to see a solution.
The integers are a cyclic group, so every subgroup is also cyclic. If we let $H$ be a subgroup of $\mathbb{Z}$, then we know there exists $d\in\mathbb{Z}$ such that $H=\left<d\right>$. This shows that $H$ equals the set of multiples of $d$, which means that $H=d\mathbb{Z}$.
Definition (Symmetric Group on $X$)
Let $X$ be any set. The $\textdef{symmetric group}$ on $X$, denoted $\sym(X)$, is the set of all permutations of $X$. We denote by $S_n$ the symmetric group on $X = \{1,2,\ldots, n\}$ and call it the symmetric group of degree $n$.
Exercise (The Symmetric Group of Degree $n$ Is A Group)
Show that $S_n$ is a group under function composition.
Click to see a solution.
We've already shown this in our work earlier in the semester. Given any two permutations of $X$, their composition is a permutation of $X$ so $S_n$ is closed. We also know that function composition is associative. The identity permutation $\text{id}_X$ definded by $\text{id}_X(x)=x$ is an element of $S_n$. The inverse of $\alpha \in S_n$ is the inverse function $\alpha^{-1}$, which is again a permutation and so in $S_n$. This shows that $S_n$ satisfies the definition of being a group.
We've already seen that we can write every permutation as a product of disjoint cycles. The next problem has you show that there are other ways to write a permutations as a product. In particular, we'll show that given a cycle of length $n$, called an $n$-cycle, we can write that cycle as a product of 2-cycles, called transpositions.
Problem 65B (optional) (Every Disjoint Cycle Can Be Written As A Product Of Transpositions)
Start by convincing yourself that $(1,2,3,4,5)=(1,5)(1,4)(1,3)(1,2)$. This shows how to write a 5-cycle as a product of transpositions (2-cycles).
- Find another way to write $(1,2,3,4,5)$ as a product of transpositions. This shows that there are multiple ways to write a cycle as a product of transpositions.
- Suppose $m,n\in \mathbb{N}$ with $m\geq n$. Also suppose that $\alpha = (a_1,a_2,a_3, \ldots, a_n)\in S_m$ is a disjoint cycle. Give a way to rewrite $\alpha$ as a product of 2-cycles.
Definition ($A_n$ - Alternating Group of Degree $n$)
Let $n\in\mathbb{N}$. Suppose that $\alpha\in S_n$.
- We say that $\alpha$ is a transposition if $\alpha$ is a cycle $(a,b)$ of length 2.
- We say that $\alpha$ is an even permutation if we can write $\alpha$ as the product of an even number of transpositions. Otherwise, we say that $\alpha$ is odd.
- The alternating group of degree $n$, written $A_n$, is the subset of $S_n$ of all even permutations.
(:include :)
Exercise
Show that each permutation below is an even permutation.
- $(1,2)(3,4)$
- $(1,2,3)$
- $(1,2)(3,4)(1,2,3)$
- $()$
- $(1,4,3,5)(2,3,1,4,7,6)$
Click to see a solution.
With each permutation, we just have two show that when we write the permutation as a product of transpositions, that the number of them is even.
- The permutation $(1,2)(3,4)$ is already written as a product of two transpositions, so it's an even permutation.
- We can write $(1,2,3)=(1,3)(1,2)$, which is two transpositions.
- Combining the two parts above, we can write $(1,2)(3,4)(1,2,3) = $(1,2)(3,4)(1,3)(1,2)$. This is a product of 4 transpositions, so the permutation is in $A_n$.
- The identity is a product of zero transpositions, which is even.
- We can write $(1,4,3,5)=(1,5)(1,3),(1,4)$ and also $(2,3,1,4,7,6)=(2,6)(2,7)(2,4)(2,1)(2,3)$. This means that $$(1,4,3,5)(2,3,1,4,7,6) = (1,5)(1,3),(1,4)(2,6)(2,7)(2,4)(2,1)(2,3), $$ which is the product of 8 transpositions.
We can show that each of the permutations above is the product of an even number of transpositions, and hence an even permutations. However, there are many other ways to write each one. Could it be that some permutations can be written as a product of an even number of transpositions, and then written a different way as an odd number of permutations? We'll leave this as an open question, and come back to it if interest and/or time permits. Regardless, we can still show that alternating group $A_n$ of degree $n$ is a subgroup of the symmetric group $S_n$. We'll do this to make sure we have some more practice with proving that subsets are subgroups.
Problem 65C (optional) (The Alternating Group Is A Subgroup Of The Symmetric Group)
Let $n\in \mathbb{N}$. Prove that $A_n$ is a subgroup of $S_n$.
- Do this using the problem The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses.
- Do this using the problem Finite Subgroup Test.
We've been studying groups in a variety of settings all semester long. We've studied simple shift permutations $H_n$, the dihedral groups $D_{2n}$, spans of a permutations $\text{span}(S)$, modular addition $\mathbb{Z}_n$, modular multiplication $U(n)$, general linear groups $GL(m,\mathbb{Z}_n)$, and more. However, each time we introduce a new group, we might ask the question, "Have we already seen this group in some other context?" Cayley graphs give us a very visual way to explore a group, and can make it extremely easy to tell when two groups that appear in completely different context might actually be "the same."
What do we mean when we say that two groups $G$ and $H$ are "the same" when the groups might on surface appear to be very different? We have already talked about what it means to have two graphs be "the same" even when the vertex structure different. We called this a graph isomorphism. The key was to create a bijection between the vertices of the graphs that preserved the edge structure. This means that the answer to whether two vertices are connected or not connected by an edge should be the same either before or after we apply the bijection. In a graph, the important relationship is the edge structure, and we want an isomorphism to preserve this structure.
Now we want to build an isomorphism between groups. The key is to create a bijection $f:(G,\cdot)\to (H,\times)$ between the underlying sets so that the group operation structures are preserved. We could perform an operation $a\cdot b$ in $G$ and then compute $f(a\cdot b)$, or we could first compute $f(a)$ and $f(b)$ and then perform the operation $f(a)\times f(b)$ in $H$. If the group structures are to be preserved, we should obtain the exact same result whether we apply the bijection first or last. We call such a map a group isomorphism.
Definition (Group Isomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{isomorphism}$ if $f$ is a bijection and $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$. We say that $G$ and $H$ are isomorphic groups, and write $G\approx H$ if there exists an isomorphism between them.
The group $H_{26}$ of simple shift permutations on the standard 26 letter alphabet is an encryption group we have learned to work with. The group operation is function composition where the composition $\phi_{k}\circ \phi_j$ is equal to $\phi_{j+k} = \phi_{j+k+26n}$ for any integer $n$. This set is very similar to the group $\mathbb{Z}_{26}$ where the operation is addition mod 26. It's so similar, that when we've drawn Cayley graphs in class, we tend to leave off the $\phi$ and just write the subscripts. Because of this similarity, they should be isomorphic groups.
Exercise (The set of simple shift permutations on 26 letters is isomorphic to $\mathbb{Z}_{26}$.)
Prove that the function $f:H_{26}\to \mathbb{Z}_{26}$ defined by $f(\phi_j)=j$ is a group isomorphism.
Click to see a solution.
We have to show two things. We must show that the function is a bijection, and that the function preserves the group operations.
- This function is a bijection because it has an inverse, namely $f^{-1}(k)=\phi_k$.
- We now have to show that the functin perserves the group operation. To show this we compute
$$f(\phi_j\circ \phi_k) = f(\phi_{j+k})= f(\phi_{(j+k)\pmod {26}}) = (j+k)\pmod {26} = (f(\phi_j)+f(\phi_k))\pmod {26}.$$ This shows that $f(\phi_j\circ \phi_k) = (f(\phi_j)+f(\phi_k))\pmod {26}$, which means the the function preserves the group operation.
This next problem asks you to show that the two groups are isomorphic.
Problem 73 (Every Finite Cyclic Group Of Order $n$ Is Isomorphic To $\mathbb{Z}_n$)
Let $H_n$ be the set of simple shift permutations on a set of $n$ letters so $H_n=\{\phi_k\mid 0\leq k\leq n\}$.
- Start by drawing the Cayley graphs of $H_7$ and $\mathbb{Z}_7$, just to make sure that the graphs are similar.
- Show that $f:H_n\to \mathbb{Z_n}$ defined by $f(\phi_k)=k$ is a group isomorphism. Remember, this means you must show that $f$ is a bijection (what's the inverse) and that $f(\phi_j\circ \phi_k) = (f(\phi_k)+f(\phi_j))\pmod n$.
- Show that if $G$ is a cyclic group of order $n$ with generator $a$, then the function $f:\mathbb{Z}_n\to G$ defined by $f(k)=a^k$ is a group isomorphism.
The previous problem shows that any time we have a cyclic group of order $n$, then we are basically working with a structure that's very similar to $\mathbb{Z}_n$. The names of the elements may be changed, but otherwise it's basically identical. The next problem has you show that a similar fact is true for infinite cyclic groups.
Problem 66 (Every Infinite Cyclic Group Is Isomorphic to $\mathbb{Z}$)
Suppose $G$ is a cyclic group of infinite order. Prove that $ \mathbb{Z}\cong G$. In other words, produce a function $f:\mathbb{Z}\to G$ and show that $f$ is an isomorphism.
Any time we use a single element $a$ of a group and construct the set $\left<a\right>$, we are creating a cyclic group. Earlier in the semester we called this the span of a single permutation. The next problem has you practice using this notation, as well as practice computing the order of an element in various groups.
Problem 67 (SKIP) (Practice With Cyclic Subgroups)
In each part below, you are given a group. Find an integer $n$ so that the given group $G$ is isomorphic to $\mathbb{Z}_n$. If you were to create an isomorphism $f:\mathbb{Z}_n\to G$, what value would you assign to $f(1)$? The first one already has an answer.
- Let $G=\langle R_{270} \rangle$ as a subgroup of $D_{4}$, the automorphisms of a square.
- We know that $R_{270}$ has order 4, so this subgroup is isomorphic to $\mathbb{Z}_4$. To obtain an isomorphism, we'd just let $f(1)=R_{270}$, as $R_{270}$ is a generator for $\langle R_{270} \rangle = \{R_{270},R_{180},R_{90},R_{0}\}$.
- Let $G=\langle R_{30} \rangle$ as a subgroup of $D_{24}$, the automorphisms of a regular 24-gon.
- Let $G=\left<\begin{bmatrix}2&1\\1&0\end{bmatrix}\right>$ in the general linear group $\text{GL}(2,\mathbb{Z}_3)$. [Hint: Just as all the previous problems, start computing powers of this matrix until you obtain the identity.]
- Let $G=\{(),(1,2,3), (1,3,2)\}$ as a subgroup of the set of all permutations of $X=\{1,2,3\}$.
- Let $G=U(7)$. [Hint: You'll need to start by finding a generator.]
- Let $G=U(17)$.
October 30
There is no class today. Please take the exam in the testing center. The exam closes Thursday night.
For more problems, see AllProblems

