Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
Here's what we'll do in class.
- Hopefully someone will have drawn their Cayley graph An Infinite Cayley Graph on the board before class starts. We'll look at it briefly.
- Have Lilia and/or Caley share their result to #4.
- Split into groups to discuss problems 1,2,7,
- Have two groups write up solutions to 5, and two write up solutions to 8.
- Present solutions to the class.
| 1 | 2 | 7 | 5 | 8 | |
| Front | Caley | Li | Justin | Rich | |
| Left | Tim | Kimberly | Bryce | Laura | |
| Back | Lilia | Cassie | Alexander | Joe | |
| Right | Terry | Carla | Brennan | Nick |
Please complete the following problem, carried over from last time.
Problem 28 (Computing Multiplicative Inverses For Small N)
To use modular arithmetic in matrix encryption, we must be able to find the modular multiplicative inverse of $a \mod n$. For each $n\leq 13$ and $a\in \mathbb{Z}_n$, we now compute the inverse of $a\mod n$ or explain why it does not have one.
- Why does $0\mod n$ never have an inverse?
- What is the multiplicative inverse of $1\mod n$?
- For $n=3$, what is the multiplicative inverse of $a=2$.
- For $n=4$, show that 2 does not have an inverse by computing $2\cdot 0$, $2\cdot 1$, $2\cdot 2$, and $2\cdot 3$ all modulo $4$. What is $3^{-1}\mod 4$?
- For each $n$ between 5 and 13, create a table that shows the inverse of each $a\in \mathbb{Z}_n$. List the elements of $\mathbb{Z}_n$ along the top row, and beneath each element list the multiplicative inverse, or cross off the number if there is no multiplicative inverse.
When you are done you should have a list of the elements of $U(n)$ for each $n$ up to 13, as well as the inverse of each element in $U(n)$. Do you see any patterns?
For $n=9$, you should obtain a table somewhat similar to the following table.
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $a^{-1}$ | x | 1 | 5 | x | 7 | 2 | x | 4 | 8 |
If $X$ is a set, and $S$ is a set of permutations of $X$, then we can create a Caley graph for the span of $S$. Here's a formal definition.
Definition (Cayley Graph Of A Span Of Permutations)
Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:
- The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
- Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
- For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.
Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.
We've done this with several automorphism groups of graphs, as well as simple shift permutation groups.
Problem 30 (Cayley Graphs Of Two Automorphism Groups)
Consider the two graphs below. Let $L$ be the automorphism group of the graph on the left, and let $R$ be the automorphism group of the graph on the right.
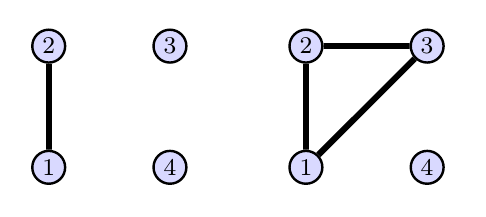
We listed the automorphisms of the graph in Problem (Automorphisms On Several Graphs With 4 Vertices).
- For the graph on the left, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in L$ so that $\text{span}(\{\alpha,\beta\})=L$. Then draw the Cayley graph of $L$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(L,\{\alpha,\beta\})$.
- For the graph on the right, use disjoint cycle notation to state two automorphisms $\alpha,\beta\in R$ so that $\text{span}(\{\alpha,\beta\})=R$. Then draw the Cayley graph of $R$ generated by $\{\alpha,\beta\}$, i.e. the Cayley graph $(R,\{\alpha,\beta\})$.
The set $X$ does not have to be finite to draw a Cayley graph, nor does $\text{span}(S)$.
Problem (An Infinite Cayley Graph)
In each scenario below, you should draw a Cayley graph.
- Let $X=\mathbb{Z}$, an infinite set. Consider the permutation $\phi_1:\mathbb{Z}\to \mathbb{Z}$ defined by $\phi_1(x)=x+1$. This permutation shifts elements in $\mathbb{Z}$ right one, with no wrap around. If we let $S=\{\phi_1\}$, give a rough sketch of the Cayley graph of $\text{span}(S)$. It's a rough sketch of the graph because there are infinitely many vertices.
- How would you change your graph in part 1 if instead you used $S=\{\phi_2,\phi_3\}$, where these are shifts right 2 and right 3 respectively?
Sometimes we can create a Cayley graph of a set of automorphisms without even knowing what the sets $X$ or $S$ are. All we need to know is how many automorphisms are in $S$, and some relationships about the automorphisms. The next problem has you examine a few more Cayley graphs.
Problem 31 (Cayley Graphs From Relations)
In each scenario below, you should draw a Cayley graph.
- Suppose that $X$ is a set, and that $S$ contains a single automorphism $s$ of $X$. Suppose also that we know $s^6$ is the identity (so following the arrow colored $c_s$ 6 times will return us to where we started). Construct a Cayley graph of $\text{span}(S)$. Is there more than one right answer to this?
- Suppose that we know $S$ contains two elements $a$ and $b$. We also know that $a^2$ and $b^4$ are both the identity. In addition, we know that $a\circ b=b\circ a$, so if we start somewhere and follow the arrows colored $c_a$ and then $c_b$, then we should end up at the same place if we followed the arrows colored $c_b$ and then $c_a$. Construct a graph that satisfies these relationships. We'll use the notation $$\left<a,b\mid a^2=id, b^4=id, a\circ b=b\circ a\right>$$ to tell us that $S=\{a,b\}$ with the relations listed after the $\mid$.
- Generalize your result above to draw a Cayley graph if instead of $b^4=id$ we have $b^k=id$.
If $X$ is a set, and $S$ is a set of permutations of $X$, then we already know how to create the span of $S$. In general, the span of $S$ will include more permutations than what we started with. However, sometimes we won't be able to obtain any new permutations by spanning $S$. When this happens, we say that the set of permutations is closed (under function composition). Here's a formal defintion.
Definition (A Closed Set Of Permutations)
We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.
The next problem has you prove some relationships between a set of permutations $S$ and its span.
Problem 32 (Relationship Between S And Its Span)
Let $S$ be a set of permutations of $X$.
- Prove that $S\subseteq \text{span}(S)$. In other words, we know that $S$ is always contained in its span; the span might be larger.
- Prove that if $\text{span}(S)\subseteq S$, then $S$ is closed.
- If $T\subseteq S$, then show that $\text{span}(T)\subseteq\text{span}(S)$.
In linear algebra, we looked at collections of vectors, and then spanned them to obtain vector spaces. Every vector space was the span of a collection of vectors. Every vector in the vector space could be written as a linear combination of the vectors used to span the span. In addition, a vector space is closed under linear combinations. This means that span of a vector space is itself. We've defined the exact same structure, but now with permutations of $X$. The next problem asks you to show that the span of a set of permutations is closed.
Problem 24 (The Span Of A Set Of Permutations Is Closed)
Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.
[Hint: You might want to let $H=\text{span}(S)$. We then need to show that $H=\text{span}(H)$, or that $\text{span}(S) = \text{span}(H)$. From the previous problem we already know that $H\subseteq \text{span}(H)$. We just need to show that $\text{span}(H)\subseteq \text{span}(S)$. So we need to show if $\sigma\in \text{span}(H)$ (it's a permutation combination of elements in $H$), then we must have $\sigma\in \text{span}(S)$ (it's a permutation combination of elements in $S$). You'll probably find yourself writing something along the lines of $\sigma = \sigma_1^{k_1}\circ \sigma_2^{k_2}\circ \cdots \sigma_n^{k_n}$ where $\sigma_i\in H$ and then have to express each $\sigma_k$ in terms of something else. ]
Definition (Integer Linear Combination Of Integers)
Let $a_1, a_2, \ldots, a_k$ be $k$ integers.
- An integer linear combination of these integers is an expression of the form $$c_1a_1+c_2 a_2+ \cdots+c_k a_k$$ where each coefficient $c_i$ is an integer.
- The span of the set of integers $\{a_1, a_2, \ldots, a_k\}$ is the set of all possible integer linear combinations of these integers, namely $$\text{span}(\{a_1, a_2, \ldots, a_k\})=\text{span}(a_1, a_2, \ldots, a_k)=\{c_1a_1+c_2 a_2+ \cdots+c_k a_k\mid c_i\in \mathbb{Z} \text{ for }1\leq i\leq k\}.$$ For ease of notation, we'll often leave off the set notation when spanning a set of integers.
- If the set $S$ of integers is infinite, then we still define the span of $S$ to be the set of all integer linear combinations of integers in $S$. Hence we know $x\in S$ if and only if there exists a natural number $k$ such that $x=c_1a_1+c_2 a_2+ \cdots+c_k a_k$ where $a_i\in S$ and $c_i\in \mathbb{Z}$ for $1\leq i\leq k$.
- When there are only two integers, we'll often use $a$ and $b$ as the integers, and $s$ and $t$ as the coefficients. So the set of all integer linear combinations of $a$ and $b$ is $$\text{span}(a,b) = \{sa+tb\mid s,t\in\mathbb{Z}\}.$$
Problem 33 (Integer Linear Combination Practice)
Complete the following.
- Compute the span of $3$, i.e. make a list of the elements in this set. In general, what is the span of a single integer $a$? (We know it by a different name.)
- What is $\text{span}(4,6)$? List the elements. Find a single number $a$ so that $\text{span}(a)=\text{span}(4,6)$.
- What is $\text{span}(4,5)$?
- Let $S=\{a_1,a_2,\ldots,a_k\}$ be a set of integers. Show that if $c\in \text{span}(S)$, then so is every multiple of $c$.
We've seen a lot of relationships in class about modular arithmetic, inverses mod n, simple shift encryption schemes, and more. The next problem makes a connection between some of these. We'll connect it to even more next time.
Problem 34 (When Does An Integer Have A Modular Multiplicative Inverse)
Let $a$ and $n$ be integers, with $n>1$. Show that the following are equivalent.
- The integer $a$ has a multiplicative inverse mod $n$
- We have $1\in \text{span}(a,n)$. In other words, we can write 1 as a linear combination of $a$ and $n$.
- We have $\text{span}(a,n)=\mathbb{Z}$. Remember that $\text{span}(a,n) = \{sa+tn\mid s,t\in\mathbb{Z}\}.$
Remember, to show that three things are equivalent you must show that each implies the other. One way to do this is show that 1 implies 2, then show that 2 implies 3, and then show that 3 implies 1. Then each implies the other.
The two problems above, together with much of our work from the previous two weeks, leads us to one of the biggest theorems in number theory. We'll prove these next time.
Theorem (The GCD Theorem)
Let $a$ and $b$ be nonzero integers. The greatest common divisor of $a$ and $b$ is an integer linear combination of $a$ and $b$, or symbolically we have $\gcd(a,b)\in\text{span}(a,b)$. In addition, the smallest positive integer linear combination of $a$ and $b$ is $\gcd(a,b)$.
Corollary (When Are Two Numbers Relatively Prime)
Two nonzero numbers $a$ and $b$ are relatively prime (i.e. their greatest common divisor is 1) if and only if there exists $s$ and $t$ such that $sa+tb=1$.
For more problems, see AllProblems
