Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
November 1
There is no prep required for today. The point is that you should be using your time to prepare for and take the exam.
I will be introducing the last half of the semester today in class. We'll be drawing a lot of Caley graphs, and using the time to introduce many of the patterns that we'll be proving during the last half of the semester. The hope is that today should be a fun introduction to the rest of the semester, with activities to work in small groups as well as a large class discussion.
If you have finished the exam and want to get started on your prep for Monday, feel free to head to Monday's prep.
November 4
The prep for today is a repeat of problems that were on the list for last Monday.
We've spent a lot of time working with cyclic groups and cyclic subgroups generated by a single element. The Well ordering principle and the GCD theorem have shown up quite a bit in our work. Let's now show that any time we start with a cyclic group, then every subgroup must also be cyclic. We've already seen this fact when we consider the problem Simple Shift Repetition where we used repeated shifting to send encrypted message to several generals.
Problem 65 (Subgroups Of Cyclic Groups Are Cyclic)
Suppose that $G$ is a cyclic group generated by $a$. Suppose that $H$ is a subgroup of $G$. Prove that there exists $k\in\mathbb{Z}$ such that $H = \left<a^k\right>$. In other words, prove that $H$ is itself a cyclic group.
Click to see a hint.
How can you get the smallest positive integer $k$ such that $a^k\in H$?
We've seen several times in class that when we compute $\text{span}(a,b)$ for integers $a$ and $b$, then their span equals $\text{span}(d)$ for a single integer $d$. In particular, we've also seen that this integer $c$ is precisely $d=\gcd(a,b)$. What if instead we wanted to look at the span of $k$ integers $\{a_1,a_2,a_3,\ldots, a_k\}$. Is there a single number $d$ that has the same span? The previous problem says that YES there must be a single number that achieves this. We call this the greatest common divisor of $a_1,a_2,a_3,\ldots, a_k$. The next exercise emphasizes this.
Exercise (The Subgroups Of $\mathbb{Z}$ are $n\mathbb{Z}$)
We know that $n\mathbb{Z}$ is a subgroup of $\mathbb{Z}$ for every integer $n$. Show that these are the only subgroups of $\mathbb{Z}$. In particular this means that the span of $k$ integers, which is a subgroup of $\mathbb{Z}$, must be equal to $d\mathbb{Z}$ for some $d\in \mathbb{Z}$.
Click to see a solution.
The integers are a cyclic group, so every subgroup is also cyclic. If we let $H$ be a subgroup of $\mathbb{Z}$, then we know there exists $d\in\mathbb{Z}$ such that $H=\left<d\right>$. This shows that $H$ equals the set of multiples of $d$, which means that $H=d\mathbb{Z}$.
Definition (Symmetric Group on $X$)
Let $X$ be any set. The $\textdef{symmetric group}$ on $X$, denoted $\sym(X)$, is the set of all permutations of $X$. We denote by $S_n$ the symmetric group on $X = \{1,2,\ldots, n\}$ and call it the symmetric group of degree $n$.
Exercise (The Symmetric Group of Degree $n$ Is A Group)
Show that $S_n$ is a group under function composition.
Click to see a solution.
We've already shown this in our work earlier in the semester. Given any two permutations of $X$, their composition is a permutation of $X$ so $S_n$ is closed. We also know that function composition is associative. The identity permutation $\text{id}_X$ definded by $\text{id}_X(x)=x$ is an element of $S_n$. The inverse of $\alpha \in S_n$ is the inverse function $\alpha^{-1}$, which is again a permutation and so in $S_n$. This shows that $S_n$ satisfies the definition of being a group.
We've already seen that we can write every permutation as a product of disjoint cycles. The next problem has you show that there are other ways to write a permutations as a product. In particular, we'll show that given a cycle of length $n$, called an $n$-cycle, we can write that cycle as a product of 2-cycles, called transpositions.
Problem 65B (optional) (Every Disjoint Cycle Can Be Written As A Product Of Transpositions)
Start by convincing yourself that $(1,2,3,4,5)=(1,5)(1,4)(1,3)(1,2)$. This shows how to write a 5-cycle as a product of transpositions (2-cycles).
- Find another way to write $(1,2,3,4,5)$ as a product of transpositions. This shows that there are multiple ways to write a cycle as a product of transpositions.
- Suppose $m,n\in \mathbb{N}$ with $m\geq n$. Also suppose that $\alpha = (a_1,a_2,a_3, \ldots, a_n)\in S_m$ is a disjoint cycle. Give a way to rewrite $\alpha$ as a product of 2-cycles.
Definition ($A_n$ - Alternating Group of Degree $n$)
Let $n\in\mathbb{N}$. Suppose that $\alpha\in S_n$.
- We say that $\alpha$ is a transposition if $\alpha$ is a cycle $(a,b)$ of length 2.
- We say that $\alpha$ is an even permutation if we can write $\alpha$ as the product of an even number of transpositions. Otherwise, we say that $\alpha$ is odd.
- The alternating group of degree $n$, written $A_n$, is the subset of $S_n$ of all even permutations.
Exercise (Practice With Even Permutations)
Show that each permutation below is an even permutation.
- $(1,2)(3,4)$
- $(1,2,3)$
- $(1,2)(3,4)(1,2,3)$
- $()$
- $(1,4,3,5)(2,3,1,4,7,6)$
Click to see a solution.
With each permutation, we just have two show that when we write the permutation as a product of transpositions, that the number of them is even.
- The permutation $(1,2)(3,4)$ is already written as a product of two transpositions, so it's an even permutation.
- We can write $(1,2,3)=(1,3)(1,2)$, which is two transpositions.
- Combining the two parts above, we can write $(1,2)(3,4)(1,2,3) = (1,2)(3,4)(1,3)(1,2)$. This is a product of 4 transpositions, so the permutation is in $A_n$.
- The identity is a product of zero transpositions, which is even.
- We can write $(1,4,3,5)=(1,5)(1,3)(1,4)$ and also $(2,3,1,4,7,6)=(2,6)(2,7)(2,4)(2,1)(2,3)$. This means that $$(1,4,3,5)(2,3,1,4,7,6) = (1,5)(1,3)(1,4)(2,6)(2,7)(2,4)(2,1)(2,3), $$ which is the product of 8 transpositions.
We can show that each of the permutations above is the product of an even number of transpositions, and hence an even permutations. However, there are many other ways to write each one. Could it be that some permutations can be written as a product of an even number of transpositions, and then written a different way as an odd number of permutations? We'll leave this as an open question, and come back to it if interest and/or time permits. Regardless, we can still show that alternating group $A_n$ of degree $n$ is a subgroup of the symmetric group $S_n$. We'll do this to make sure we have some more practice with proving that subsets are subgroups.
Problem 65C (optional) (The Alternating Group Is A Subgroup Of The Symmetric Group)
Let $n\in \mathbb{N}$. Prove that $A_n$ is a subgroup of $S_n$.
- Do this using the problem The Subgroup Test - Subgroups Are Subsets That Are Closed Under Products And Taking Inverses.
- Do this using the problem Finite Subgroup Test.
Click to see a hint.
What is the inverse of $(1,2)$? If $\alpha=(a,b)$ is a transposition, what is the inverse?
We've been studying groups in a variety of settings all semester long. We've studied simple shift permutations $H_n$, the dihedral groups $D_{2n}$, spans of a permutations $\text{span}(S)$, modular addition $\mathbb{Z}_n$, modular multiplication $U(n)$, general linear groups $GL(m,\mathbb{Z}_n)$, and more. However, each time we introduce a new group, we might ask the question, "Have we already seen this group in some other context?" Cayley graphs give us a very visual way to explore a group, and can make it extremely easy to tell when two groups that appear in completely different context might actually be "the same."
What do we mean when we say that two groups $G$ and $H$ are "the same" when the groups might on surface appear to be very different? We have already talked about what it means to have two graphs be "the same" even when the vertex structure different. We called this a graph isomorphism. The key was to create a bijection between the vertices of the graphs that preserved the edge structure. This means that the answer to whether two vertices are connected or not connected by an edge should be the same either before or after we apply the bijection. In a graph, the important relationship is the edge structure, and we want an isomorphism to preserve this structure.
Now we want to build an isomorphism between groups. The key is to create a bijection $f:(G,\cdot)\to (H,\times)$ between the underlying sets so that the group operation structures are preserved. We could perform an operation $a\cdot b$ in $G$ and then compute $f(a\cdot b)$, or we could first compute $f(a)$ and $f(b)$ and then perform the operation $f(a)\times f(b)$ in $H$. If the group structures are to be preserved, we should obtain the exact same result whether we apply the bijection first or last. We call such a map a group isomorphism.
Definition (Group Isomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{isomorphism}$ if $f$ is a bijection and $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$. We say that $G$ and $H$ are isomorphic groups, and write $G\approx H$ if there exists an isomorphism between them.
The group $H_{26}$ of simple shift permutations on the standard 26 letter alphabet is an encryption group we have learned to work with. The group operation is function composition where the composition $\phi_{k}\circ \phi_j$ is equal to $\phi_{j+k} = \phi_{j+k+26n}$ for any integer $n$. This set is very similar to the group $\mathbb{Z}_{26}$ where the operation is addition mod 26. It's so similar, that when we've drawn Cayley graphs in class, we tend to leave off the $\phi$ and just write the subscripts. Because of this similarity, they should be isomorphic groups.
Exercise (The set of simple shift permutations on 26 letters is isomorphic to $\mathbb{Z}_{26}$.)
Prove that the function $f:H_{26}\to \mathbb{Z}_{26}$ defined by $f(\phi_j)=j$ is a group isomorphism.
Click to see a solution.
We have to show two things. We must show that the function is a bijection, and that the function preserves the group operations.
- This function is a bijection because it has an inverse, namely $f^{-1}(k)=\phi_k$.
- We now have to show that the functin perserves the group operation. To show this we compute
$$f(\phi_j\circ \phi_k) = f(\phi_{j+k})= f(\phi_{(j+k)\pmod {26}}) = (j+k)\pmod {26} = (f(\phi_j)+f(\phi_k))\pmod {26}.$$ This shows that $f(\phi_j\circ \phi_k) = (f(\phi_j)+f(\phi_k))\pmod {26}$, which means the the function preserves the group operation.
This next problem asks you to show that the two groups are isomorphic.
Problem 73 (Every Finite Cyclic Group Of Order $n$ Is Isomorphic To $\mathbb{Z}_n$)
Let $H_n$ be the set of simple shift permutations on a set of $n$ letters so $H_n=\{\phi_k\mid 0\leq k\leq n\}$.
- Start by drawing the Cayley graphs of $H_7$ and $\mathbb{Z}_7$, just to make sure that the graphs are similar.
- Show that $f:H_n\to \mathbb{Z_n}$ defined by $f(\phi_k)=k$ is a group isomorphism. Remember, this means you must show that $f$ is a bijection (what's the inverse) and that $f(\phi_j\circ \phi_k) = (f(\phi_k)+f(\phi_j))\pmod n$.
- Show that if $G$ is a cyclic group of order $n$ with generator $a$, then the function $f:\mathbb{Z}_n\to G$ defined by $f(k)=a^k$ is a group isomorphism.
The previous problem shows that any time we have a cyclic group of order $n$, then we are basically working with a structure that's very similar to $\mathbb{Z}_n$. The names of the elements may be changed, but otherwise it's basically identical. The next problem has you show that a similar fact is true for infinite cyclic groups.
Problem 66 (Every Infinite Cyclic Group Is Isomorphic to $\mathbb{Z}$)
Suppose $G$ is a cyclic group of infinite order. Prove that $ \mathbb{Z}\cong G$. In other words, produce a function $f:\mathbb{Z}\to G$ and show that $f$ is an isomorphism.
Any time we use a single element $a$ of a group and construct the set $\left<a\right>$, we are creating a cyclic group. Earlier in the semester we called this the span of a single permutation. The next problem has you practice using this notation, as well as practice computing the order of an element in various groups.
Problem 67 (SKIP) (Practice With Cyclic Subgroups)
In each part below, you are given a group. Find an integer $n$ so that the given group $G$ is isomorphic to $\mathbb{Z}_n$. If you were to create an isomorphism $f:\mathbb{Z}_n\to G$, what value would you assign to $f(1)$? The first one already has an answer.
- Let $G=\langle R_{270} \rangle$ as a subgroup of $D_{4}$, the automorphisms of a square.
- We know that $R_{270}$ has order 4, so this subgroup is isomorphic to $\mathbb{Z}_4$. To obtain an isomorphism, we'd just let $f(1)=R_{270}$, as $R_{270}$ is a generator for $\langle R_{270} \rangle = \{R_{270},R_{180},R_{90},R_{0}\}$.
- Let $G=\langle R_{30} \rangle$ as a subgroup of $D_{24}$, the automorphisms of a regular 24-gon.
- Let $G=\left<\begin{bmatrix}2&1\\1&0\end{bmatrix}\right>$ in the general linear group $\text{GL}(2,\mathbb{Z}_3)$. [Hint: Just as all the previous problems, start computing powers of this matrix until you obtain the identity.]
- Let $G=\{(),(1,2,3), (1,3,2)\}$ as a subgroup of the set of all permutations of $X=\{1,2,3\}$.
- Let $G=U(7)$. [Hint: You'll need to start by finding a generator.]
- Let $G=U(17)$.
November 6
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
Problem 69 (Cayley Tables And Isomorophisms On A Group Of Order 4)
In the problem Orders Of $\mathbb{Z}_n$ And $U(n)$ And Their Elements we computed the orders of $U(n)$ of $n$ from 2 to 10. The groups $U(5)$, $U(8)$, and $U(10)$ all have order 4 (they have four elements). For $U(5)$, we can construct a multiplication table (called a Cayley table) that represents the binary operation of the group. We create this table exactly as we created the times tables in grade school, where we put the product $ab$ in the row corresponding to $a$ and the column corresponding to $b$. The table for $U(5)$ is shown below. $$\begin{array}{c|cccc} \cdot \text{ mod } 5 & 1&2&3&4 \\ \hline\hline 1 & 1&2&3&4 \\ 2 & 2&4&1&3 \\ 3 & 3&1&4&2 \\ 4 & 4&3&2&1 \\ \end{array}$$
- Construct a multiplication table, i.e. Cayley table, for $U(8)$ and $U(10)$. Which of these groups is isomorphic to $U(5)$?
- Let $G = \{a,b,c,d\}$ and $H=\{r,s,t,u\}$ and define the operation $*$ on $G$ in the table on the left below, and the operation $\times$ on $H$ by the table on the right below. $$ \begin{array}{c|cccc} * & a&b&c&d \\ \hline\hline a & a&b&c&d \\ b & b&d&a&c \\ c & c&a&d&b \\ d & d&c&b&a \\ \end{array} \quad\quad\quad \begin{array}{c|cccc} \times & r&s&t&u \\ \hline\hline r & t&u&r&s \\ s & u&t&s&r \\ t & r&s&t&u \\ u & s&r&u&t \\ \end{array}.$$ For each group, which element is the identity element? Which group is isomorphic to $U(8)$?
- Let $K=\{1,-1,i,-i\}$, which is a subset of the complex numbers (recall that $i=\sqrt{-1}$ and $i^2=-1$). Construct a multiplication table for $K$, and show that $K$ is isomorphic to one of the groups above.
To show that two groups are isomorphic, we must show that there is a bijection between them that preserves the group structures. In linear algebra, we encounter maps that preserve the group structure, but are not necessarily bijections. We called such maps linear transformations in linear algebra. In a general group setting, we call these maps homomorphisms. Here's a formal definition.
Definition (Group Homomorphism)
Let $(G,\cdot)$ and $(H,\times)$ be groups. We say that the function $f:G\to H$ is a group $\textdef{homomorphism}$ if $f$ preserves the group structures, which means $f(a\cdot b)=f(a)\times f(b)$ for every $a,b\in G$.
When we want to know if a matrix is invertible, or serves as a valid encryption key, we can discover this by computing the determinant. If the determinant of the matrix is non zero, has a multiplicative inverse, then we can invert this matrix. We shows this was true as well even when working with matrix encryption mod $n$.
Problem 70 (The Determinant Map Is A Homomorphism)
Let $n$ be an integer greater than 1, and consider the general linear group $\text{GL}(2,\mathbb{Z}_n)$ of two by two invertible matrices mod $n$. Let $f$ be the determinant map $f:\text{GL}(2,\mathbb{Z}_n)\to U(n)$ defined by $f(A)=\det A$, i.e. defined by $$f\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)= (ad-bc)\pmod n.$$ Show that $f$ is a homomorphism. Prove this result by direct computation, rather than by claiming it was already shown to be true in a previous course.
The set of matrices that have determinant one is a special group of matrices. We can use this group of matrices to learn quite a bit about all matrices. Here's a formal definition.
Definition (Special Linear Group $\text{SL}(m,\mathbb{Z}_n)$)
We have already defined the general linear group $\text{GL}(m,\mathbb{Z}_n)$ to be the set of $m$ by $m$ invertible matrices with coefficients in $\mathbb{Z}_n$, together with the binary operation of matrix multiplication mod $n$. The set of matrices in $\text{GL}(m,\mathbb{Z}_n)$ that have determinant 1 is called the special linear group, and we write $$\text{SL}(m,\mathbb{Z}_n)=\left\{ a\in \text{GL}(m,\mathbb{Z}_n) \mid \det(a)=1 \right\}.$$
Problem 71 (The Special Linear Group Is A Subgroup Of The General Linear Group)
Prove that $\text{SL}(m,\mathbb{Z}_n)$ is a subgroup of $\text{GL}(m,\mathbb{Z}_n)$. Why is the set of matrices whose determinant equals 2 not a subgroup of the general linear group?
Given $m,n\geq 2$, how many elements are in $GL(2,\mathbb{Z}_n)$? In other words, how many different matrix encryption keys are there, given the size of the matrix and what coefficients we'll allow. This is a nontrivial problem, but its answer is provides a key to knowing how to decrypt a message by brute force. We'll find that knowing something about the special linear groups will help us answer this question. First, let's make an observation that should simplify some computations if we assume that $n$ is prime.
Exercise (The Order Of $U(p)$ When $p$ Is Prime)
If $p$ is a prime, then what is the order of $U(p)$? In other words, what is the Euler $\varphi$ function at $p$, namely what is $\varphi(p)$.
Click to see a solution.
If $p$ is prime, then every positive integer less than $p$ is relatively prime to $p$. This means that $U(p)=\{1,2,3,4,\ldots, p-1\}$, which means $|U(p)|=p-1$. The Euler $\varphi$ function is just the number of elements in $U(n)$, so we have $\varphi(p)=p-1$ for primes $p$.
If $n$ is not prime, then the set $U(n)$ does not contain every positive integer less than $n$, which makes it harder to work with $U(n)$ when $n$ is not prime.
Problem 74 (Conjecturing The Order Of General Linear Groups)
Let's focus on 2 by 2 matrices with entries in $\mathbb{Z}_p$ where $p$ is a prime. So we let $p$ be a prime and consider $G = \text{GL}(2,\mathbb{Z}_p)$.
- Here is a list of all 81 of the 2 by 2 matrices with entries in $\mathbb{Z}_3$. Underneath that list you'll see the determinant of each matrix has already been computed for you. How many matrices have determinant 1, in other words how many matrices are in $\text{SL}(2,\mathbb{Z}_3)$. How many matrices are invertible, i.e. how many matrices are in $\text{GL}(2,\mathbb{Z}_3)$? What patterns did you use to help you count?
n=3 matrices=[]; for i in [0..n-1]: for j in [0..n-1]: tempmatrices=[] for k in [0..n-1]: for l in [0..n-1]: tempmatrices.append(matrix(2,2,[i,j,k,l])) matrices.append(tempmatrices) show(table(matrices)) dets=[]; for i in [0..n-1]: for j in [0..n-1]: tempdets=[] for k in [0..n-1]: for l in [0..n-1]: tempdets.append(matrix(2,2,[i,j,k,l]).det().mod(n)) dets.append(tempdets) show(table(dets))
- This sage code below repeats the above with $n=5$. Use this to count how many matrices have determinant 1 (are in $\text{SL}(2,\mathbb{Z}_5)$) and then how many are invertible (are in $\text{GL}(2,\mathbb{Z}_5)$). What patterns did you use to help you count?
n=5 #Change this number as needed. matrices=[]; for i in [0..n-1]: for j in [0..n-1]: tempmatrices=[] for k in [0..n-1]: for l in [0..n-1]: tempmatrices.append(matrix(2,2,[i,j,k,l])) matrices.append(tempmatrices) #show(table(matrices)) #Uncomment this line (remove the #) if you want to see all the matrices. dets=[]; for i in [0..n-1]: for j in [0..n-1]: tempdets=[] for k in [0..n-1]: for l in [0..n-1]: tempdets.append(matrix(2,2,[i,j,k,l]).det().mod(n)) dets.append(tempdets) show(table(dets))
- You can modify the sage code above to let $n=7, 11, 13,$ etc. How many matrices are in $\text{SL}(2,\mathbb{Z}_7)$ and $\text{GL}(2,\mathbb{Z}_7)$? What patterns did you use to help you count?
- If $p$ is a prime, make a conjecture about the order of $\text{SL}(2,\mathbb{Z}_p)$ and the order of $\text{GL}(2,\mathbb{Z}_p)$. You do not have to prove your conjecture.
November 8
You should have noticed in the problem Conjecturing The Order Of General Linear Groups that the number of matrices with determinant 1 always equals the number of matrices with a fixed determinant $k$. What we would like to do next is find a nice way to prove this. To do so, we first need to talk about the product of a set and an element. This will allow us to take any matrix $a$ and multiply it by each matrix with determinant 1 to obtain all matrices whose determinants match $a$. Here's the formal definition of the product of a set and an element.
Definition (The Product Of A Set And An Element)
Let $H$ be a subset of a group $G$ and let $a\in G$. Then we define the product $Ha$ and $aH$ to be the sets $$Ha = \{ha \mid h\in H\}\quad \text{and}\quad aH=\{ah\mid h\in H\}.$$ If the group $G$ is Abelian, then we generally use the operation $+$ instead of $\cdot$, and so we'll write $H+a$ instead of $Ha$ and we'll write $a+H$ instead of $aH$. However, since the operation is commutative, we know that $a+h=h+a$, and so we have $$H+a = \{h+a \mid h\in H\} = \{a+h\mid h\in H\}=a+H.$$
Problem 75 (The Set Product $Ha$ Preserves Determinants)
Let $m=2$ and let $p$ be a prime (it could be any integer, but $U(p)$ is easier to understand when $p$ is prime). Let $H=\text{SL}(2,\mathbb{Z}_p)$ and $G=\text{GL}(2,\mathbb{Z}_p)$. Let $a\in G$, so $a$ is a 2 by 2 invertible matrix. Recall that the set $Ha$ is the set $$Ha=\{ha\mid h\in H\},$$ so to obtain an element in $Ha$, we just take a matrix $h$ with determinant 1 and then multiply it on the right by the matrix $a$.
- Let $b\in GL(2,\mathbb{Z}_p)$. Prove that $b\in Ha$ if and only if $\det(b)=\det(a)$.
- When you prove if $b\in Ha$ then $\det(b)=\det(a)$, you'll show that every matrix in $Ha$ has the same determinant as $a$.
- When you prove if $\det(b)=\det(a)$ then $b\in Ha$, you'll show that every matrix with the same determinant as $a$ must be in $Ha.$
- Prove that the function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection. (What is the inverse of multiplying on the right by $a$?)
- Explain why $|H|=|Ha|$, in other words the number of matrices whose determinant equals 1 is the same as the number of matrices whose determinant equals $\det(a)$.
Now that we've got a little practice with homomorphisms, we need to prove some general facts about them. In particular, it would be nice to know how homomorphisms interact with the identity, and how they interact with inverse. For the determinant map, we know that the determinant of the identity is 1, which means that the determinant of the identity matrix is the identity in $U(p)$. The homomorphism mapped the identity to the identity. In addition, if the determinant of a matrix $A$ is $k$, then the determinant of the inverse of $A$ is $k^{-1}$. This shows that the determinant of an inverse is the inverse of the determinant. The next problem has you show that these two facts are true for any homomorphism.
Problem 76 (Homomorphisms Preserve The Identity And Inverses)
Suppose that $f:G\to H$ is a homomorphism, and that $e_G$ and $e_H$ are the identities of $G$ and $H$ respectively.
- Prove that $f(e_G)=e_H$.
- In addition show that $f(a^{-1})=(f(a))^{-1}$.
Click to see a hint.
You know that $e_Ge_G=e_G$. How does $f(e_Ge_G)=f(e_G)$ help you know that $f(e_G)=e_H$? Remember to use the fact that $f$ is a homomorphism.
To show that $f$ preserves inverses, think about how you can prove that the determinant of an inverse is the inverse of the determinant. If we have two matrices $A$ and $B$ then we know that $|AB|=|A||B|$. If we know that $B=A^{-1}$, then we have $AA^{-1}=I$ and so we have $|A||A^{-1}|=|I|=1$. Since we know that $|A||A^{-1}|=1$, we can just multiply both sides on the left by $|A|^{--1}$ to get $|A^{-1}|=|A|^{-1}$. If you mimic this process with an arbitrary homomorphism, you should find the solution for any homomorphism. Just replace $|A|$ with $f(a)$. What you did in linear algebra is the key to the more generalized notion of a homomorphism.
Recall the determinant map. The special linear group was the set of things that got mapped to the identity in $U(p)$. In Linear algebra, you looked at linear transformations and defined the kernel of the linear transformation to be the set of vectors that mapped to zero. This is precisely the set of vectors that mapped to the additive identity. The set of vectors which map to the identity is a special set, that we now define to be the kernel of a homomorphism. The kernel is the center, or core, of a seed, and we'll soon see that understanding the kernel of a homomorphism is central, or core, to understanding most problems in mathematics. Please ask me in class to discuss applications of this idea that you have seen in other courses. You've been studying the kernel of a homomorphism for quite a while, without every putting a name to it.
Definition (Kernel Of A Homomorphism)
The kernel of a homomorphism $f:G\to H$ is the set of elements in $G$ that are mapped to the identity $e_H\in H$. In symbols, we'll write the kernel of $f$ as $$\ker(f)=f^{-1}(e_H) = \{g\in G\mid f(g)=e_H\}.$$
For any prime $p$, if we let let $G=GL(2,\mathbb{Z}_p)$ and we consider the homomorphism $f:G\to U(p)$ which is the determinant map, then we've already shown that the kernel of the determinant map, namely $f^{-1}(1)$, is the special linear group $SL(2,\mathbb{Z}_p)$. The kernel of the map was a subgroup of $G$. The next problem has you show this result in general, namely that the kernel of any homomorphism $f:G\to H$ is always a subgroup of $G$. Your proof should be almost identical to what you did for the special linear group.
Problem 77 (The Kernel Of A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism and that $e_H$ is the identity in $H$. Prove that the kernel of $f$, namely $\ker f$ or $f^{-1}(e_H)$, is a subgroup of $G$.
For the rest of today, we'll be looking at the set products $aH$ and $Ha$ and what they physical mean in Cayley graphs. Once we can see these sets in Cayley graphs, we'll have a very visual way to describe the remainder of the ideas in this course. The sets $aH$ and $Ha$ are so crucial to the rest of this course that they have been given a name and are referred to as cosets. Here is a formal definition
Definition (Cosets $Ha$ and $aH$)
Let $G$ be a group and let $H$ be a subgroup of $G$. Let $a\in G$. We say that the set product $aH$ is a left coset of $H$ and the set product $Ha$ is a right coset of $H$. Remember that when the group is Abelian and we use the symbol $+$ to represent the group operation, then we write $a+H$ for the left cosets and $H+a$ for the right cosets.
We have already seen cosets when working with matrices that have the same determinant. We've also seen cosets already when working with modular arithmetic. This next exercise has you practice this.
Exercise (Practice With Cosets Of $3\mathbb{Z}$)
Let $G=\mathbb{Z}$ and let $H=3\mathbb{Z}$, the multiples of $3$.
- List the elements of $0+H$, $1+H$, $2+H$, $3+H$, $4+H$, $5+H$, $17+H$, and $-11+H$.
- How many different sets did you get?
Click to see a solution.
We know that $H=\{\ldots,-6, -3, 0, 3, 6, \ldots\}$. Adding 1 to each entry gives $H=\{\ldots,-5, -2, 1, 4, 7, \ldots\}$, which is the same as the set of integers whose remainder is 1 after dividing by 3. Similarly we have $$\begin{align} 0+H &= \{\ldots,-6, -3, 0, 3, 6, \ldots\}, \\ 1+H &= \{\ldots,-5, -2, 1, 4, 7, \ldots\}, \\ 2+H &= \{\ldots,-4, -1, 2, 5, 8, \ldots\}, \\ 3+H &= \{\ldots,-3, 0, 3, 6, 9, \ldots\} = \{\ldots,-6, -3, 0, 3, 6, \ldots\} = 0+H,\\ 4+H &= \{\ldots,-2, 1, 4, 7, 10, \ldots\} = \{\ldots,-5, -2, 1, 4, 7, \ldots\} = 1+H,\text{ and}\\ 5+H &= \{\ldots,-1, 2, 5, 8, 11, \ldots\} = \{\ldots,-4, -1, 2, 5, 8, \ldots\} = 2+H. \end{align}$$ In our computations above, we see that $k+H$ is equivalent to $k\pmod 3+H$. Since $17\pmod 3=2$ and $-11\pmod 3=1$, we have that $17+H = 2+H$ and we also have $-11+H = 1+H$.
There are only three different cosets. The cosets are $0+H$, $1+H$, and $2+H$. Every other coset is equal to one of these.
Definition (Identification Graph Using Cosets)
Let $G$ be a group, and let $\mathcal{G}=(G,S)$ be the Cayley graph of $G$ using the elements in $S$ to construct the colored arrows. Let $H$ be a subgroup of $G$. The identification graph of $G$ using the right cosets of $H$ is a colored directed graph such that
- The set of vertices is the set of right cosets $\{Ha\mid a\in G\}$, and
- We draw a colored arrow from the coset $Ha$ to the coset $Hb$ if and only if there exists a colored arrow $(c,d)$ with $c\in Ha$ and $d\in Hb$ in the original Cayley graph.
If instead of using right cosets, we used left cosets $aH$ as the vertices, then we'd call the graph the identification graph of $G$ using the left cosets of $H$.
The identification graphs just described will generally be a smaller graphs than the original graph. Sometimes those graphs will themselves be Cayley graphs, and sometimes they won't. One of our goals right now is to determine under which conditions we'll obtain a Cayley graph after computing an identification graph.
Problem 78 (Exercise - Solution provided) (Practice With Identification Graphs On An Abelian Group)
Let $G = U(15)$. Consider the subgroups $A=\left<4\right> = \{1,4\}$ and $B= \left<14\right> = \{1,14\}$. We'll use the set $S=\{7,11\}$ to draw the Cayley graph of $G$.
- Start by drawing the Cayley graph of $G$ with generators in $S$. You can check your answer with the Sage code at the end of this problem.
- For each $g\in G$, compute the right cosets $Ag$ of $A$. Draw the identification graph of $G$ using right cosets of $A$. You should get a graph with 4 vertices (each vertex should have two numbers in it). The graph should look like the Cayley graph of $U(8)$ using the generating set $S=\{3,5\}$, shown in the sage code below.
- For each $g\in G$, compute the left cosets $gA$ of $A$. Draw the identification graph of $G$ using left cosets of $A$.
- For each $g\in G$, compute the right cosets $Bg$ of $B$. Draw the identification graph of $G$ using right cosets of $B$. Again you should get a graph with 4 vertices, however your graph should not be the same as that in part 2. You should obtain something similar to the graph of $U(10)$ using the generating set $S=\{3,9\}$, shown in the sage code below. Click "Evaluate" a few times as the way the computer displays this graph can change.
- For each $g\in G$, compute the left cosets $gB$ of $B$. Draw the identification graph of $G$ using left cosets of $B$.
- Why are the answer to 2 and 3 the same? Why are the answers to 4 and 5 the same?
n=15
S=[7,11]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
n=8
S=[3,5]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
n=10
S=[3,9]
Zn = Integers(n)
Un = [int(x) for x in Zn if gcd(ZZ(x), n) == 1] #This creates Un
CG=DiGraph([Un,lambda i,j:False])
for k in S:
CGk=DiGraph([Un,lambda i,j: mod(j*inverse_mod(i,n),n)==k])
for u,v,l in CGk.edges():
CGk.set_edge_label(u,v,k)
CG.add_edges(CGk.edge_iterator())
print("Here is a graph of U("+str(n)+") using the generating set "+str(S))
CG.graphplot(color_by_label=True,edge_labels=True).show()
Problem 79 (Exercise - Solution Provided) (Practice With Identification Graphs On A Non Abelian Group)
Let $G$ be the automorphisms of the square, i.e. the dihedral group of order 8. Consider the subgroups $A=\left<R_{180}\right> = \{R_0,R_{180}\}$ and $B= \left<H\right> = \{R_0,H\}$. We'll use the set $S=\{R_{90}, V\}$ to draw the Cayley graph of $G$.
- Start by drawing the Cayley graph of $G$ with generators in $S$. You can check your answer with the Sage code at the end of this problem.
- For each $g\in G$, compute the right cosets $Ag$ of $A$. Draw the identification graph of $G$ using right cosets of $A$.
- For each $g\in G$, compute the left cosets $gA$ of $A$. Draw the identification graph of $G$ using left cosets of $A$.
- For each $g\in G$, compute the right cosets $Bg$ of $B$. Draw the identification graph of $G$ using right cosets of $B$.
- For each $g\in G$, compute the left cosets $gB$ of $B$. Draw the identification graph of $G$ using left cosets of $B$.
- Make a conjecture about what happens with identification graphs when $gA=Ag$.
R90="(1,2,3,4)" V="(1,4)(2,3)" S=[R90,V] G=PermutationGroup(S) G.cayley_graph().show(color_by_label=True)
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
Please also let me know which other problems from this list you are ready to present. Problem 3 has quite a few people ready, but I'd like to see a few more. It's almost the same as what we did in class today with $\mathbb{Z}_n$, just this time it's infinite.
November 11
Problem 80 (When Does $H=Ha$)
Let $H$ be a nonempty subset of a group $G$. Prove that $H$ is a subgroup of $G$ if and only if $Ha=H$ for every $a\in H$.
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Problem (How Do You Build A Multiplication Table From A Cayley Graph)
Each of the Cayley graphs below is the Cayley graph of a group. However, the original labels on the vertices were lost, as well as the group operation table. However, from the Cayley graph alone we can reconstruct the group operation by constructing a multiplication table. We start by randomly choosing one point in the graph to be the identity $e$. There are two colors which we'll call $a$ and $b$. So if we start at $e$ and follow the arrow colored $a$, we should end at the group element $a$. Similarly, starting from $e$ and following the arrow colored $b$ gets us to the group element $b$. In both graphs below, starting at $e$ and following $a$ twice gets us to $c$, so we know that $a\cdot a=c$. If we start at any point $x$, then the product $ax$ means to start at $x$ and follow $a$. Because we know $c=a\cdot a$, then the product $cx=aax$ means start at $x$ and follow $a$ twice. Since we know $c=aae$ and $d=abe$ (start at $e$ and then follow $b$ then $a$), then the product $dc=abeaae$ which means start at $e$, then follow $a$ then $a$ then $b$ then $a$, which ends us at $b$. Use the Cayley graphs below to create the multiplication table for each group.
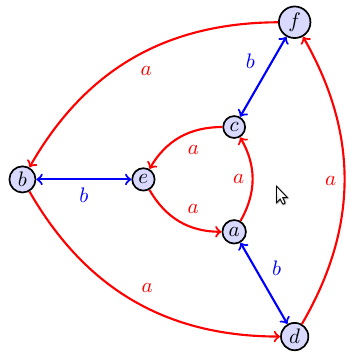
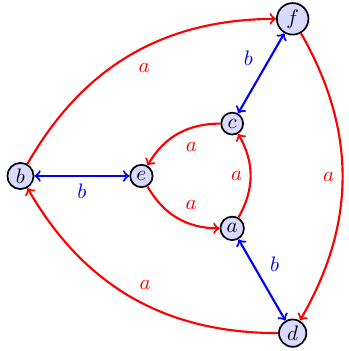
$$\begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&d&e&f&b\\ b & b& & & & &\\ c & c& & & &b&\\ d & d& & &b& &\\ f & f& & & & &\\ \end{array} \quad\quad\quad\quad\quad\quad\quad\quad\quad \begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a& & & & &\\ b & b& & & & &\\ c & c& & & & &\\ d & d& & & & &\\ f & f& & & & &\\ \end{array} $$
Click to see a solution. We won't have anyone present this one in class.
The correct Cayley tables are shown below. $$\begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&d&e&f&b\\ b & b&d&e&f&a&c\\ c & c&e&f&a&b&d\\ d & d&f&a&b&c&e\\ f & f&b&c&d&e&a\\ \end{array} \quad\quad\quad\quad\quad\quad\quad\quad\quad \begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&f&e&b&d\\ b & b&d&e&f&a&c\\ c & c&e&d&a&f&b\\ d & d&f&c&b&e&a\\ f & f&b&a&d&c&e\\ \end{array} $$
Problem (Visualizing Cosets In A Cayley Graph)
The graph below is the Cayley graph of a group of order 12. A multiplication table for this group would consist of 144 entries. On this problem, we will visually construct the cosets of several subgroups of $G$ to illustrate how the cosets create a partition of $G$. Your goal is to understand visually the difference between right cosets $Hg$ and left cosets $gH$. You will need 4 colors to complete this problem.
- Let $H=\left<a\right> = \{e,a,a^2\}$. Compute all the right cosets $Hx$ of $H$ for $x\in G$. You should obtain 4 different right cosets. Use the graph below on your left and color the vertices so that two vertcies are colored the same if and only if they are in the same right coset. Then repeat this with the left cosets $gH$ of $H$, and color your vertices in the graph on the right.


- Now let $H=\left<b\right> = \{e,b\}$ and repeat part 1. Because $|H|=2$, you should obtain 6 cosets.


- Now let $H= \{e,b,i,k\}$ and repeat part 1. Because $|H|=4$, you should obtain 3 cosets.


- Now draw the 6 identification graphs obtained by considering either right cosets or left cosets for each of the subgroups above. You should notice that the only identification graph that is a Cayley graph is the last one where $H= \{e,b,i,k\}$. This happens precisely because the left and right cosets are the same, namely $gH=Hg$ for every $g\in G$. This is not a coincidence.
Let's now turn our attention back to homomorphisms. We'll see very soon that there is a big connection between homomorphisms and cosets. For today, let's just focus on some more properties of homomorphisms, namely that homomorphisms preserve subgroups. If you've forgotten the definition of the image of a set under a function, then here is a reminder.
Definition (Definition.The image of a function $f(A)$)
Let $f:G\to H$ be a function and let $A$ be subset of $G$. Recall that the image of $A$ under $f$ is the set $$f(A)=\{f(a)\mid a\in A\}.$$
If the set $A$ is a subgroup, then we would expect that a homomorphism maps the subgroup $A$ to a subgroup of $H$. This is precisely what the next problem asks you to show.
Problem 81 (The Image Of A Subgroup Under A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism. Let $A$ be a subgroup of $G$. Show that $f(A)$ is a subgroup of $H$.
We now generalize some facts that we learned about the determinant map. We have already shown that the determinant map breaks up the set of possible matrices into equally sized cosets, where each coset consists of matrices of the same determinant. The next problem has you show that this property was not dependent on the determinant map, rather it has to do with the fact that the special linear group is a subgroup, and nothing more. You should find that your work on the problem The Set Product $Ha$ Preserves Determinants can almost be copied directly over to solve the next problem.
Problem 82 (Properties Of Cosets)
Let $G$ be a group, and let $H$ be a subgroup of $G$. Let $a,b \in G$. Prove the following:
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
As a last problem for today, let's generalize something we proved earlier in the semester. We've already shown that the intersection of two subgroups of a group is again a subgroup. What we'd like to show now is that the intersection of any collection of subgroups is again a subgroup of $G$. This fact is true whether the number of subgroups is finite, countable, or uncountable. If you do not remember the definition the intersection of a collection of subsets, here is a reminder.
Definition (Intersection Of A Collection Of Sets)
If $A$ and $B$ are a two sets, we say that $x\in A\cap B$ if and only if $x\in A$ and $x\in B$. If $\mathscr{B}$ is a collection of sets, then we say that $x$ is an element of the interesection of the collection of sets if and only if $x\in B$ for each $B\in \mathscr{B}$. We write this in set builder notation as $$\ds\bigcap_{B\in \mathscr{B}}B = \{x\mid x\in B \text{ for each }B\in \mathscr{B} \}.$$
Your proof to the problem Problem.TheIntersectionOfTwoSubgroups should provide you with a solution to this problem. You just need to change the fact that you are not working with two subgroups anymore, rather you are working with some nonempty collection of subgroups. You can find a solution to that problem on the key to the midterm, if you don't remember.
Problem (The Intersection Of Any Nonempty Collection Of Subgroups Is A Subgroup)
Let $G$ be a group. Suppose that we have a nonempty collection $\mathscr{B}$ of subgroups of $G$. Prove that the intersection of this collection of subgroups of $G$ is a subgroup of $G$. Symbolically, we can write this as $\ds\bigcap_{H\in \mathscr{B}}H$ is a subgroup of $G$.
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
November 13
Over the last few days we have been studying cosets quite a bit. We've seen that when we create an identification graph of $G$ using right cosets of $H$, we sometimes get a Cayley graph, and we sometimes don't. Today, we'll be focusing on the questions, "When is an identification graph of $G$ using cosets of $H$ another Cayley graph?" To answer this question, we'll need to explore the properties of cosets in depth.
- If $H$ is a subgroup of $G$ and $a\in H$, then $H\subseteq Ha$.
- If $Ha=H$ for every $a\in H$, then $H$ is a subgroup of $G$.
Problem 80 (When Does $H=Ha$)
Let $H$ be a nonempty subset of a group $G$. Prove that $H$ is a subgroup of $G$ if and only if $Ha=H$ for every $a\in H$.
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=hb$ for some $h\in H$).
When working with the determinant map $f:GL(2,\mathbb{Z}_p)\to U(p)$, we have already shown that the kernel of this map is the special linear group $K=SL(2,\mathbb{Z}_p)$. We've also shown that the coset $Ka$ equals the set of all matrices whose determinant matches the determinant of $a$. Another way to say this is that $Ka$ equals the set of values $b\in G(2,\mathbb{Z}_p)$ such that $f(b)=f(a)$. A similar argument would show that $aK$ is the exact same set, which means we have $Ka=aK$. The next problem has you show that for any homomorphism $f:G\to H$ with kernel $K$, we always have $Ka=aK$ and that $Ka$ equals the set of $b\in G$ such that $f(b)=f(a)$.
Problem 83 (The Right And Left Cosets Of The Kernel Are Equal)
Suppose that $f:G\to H$ is a homomorphism. Let $K$ be the kernel of $f$ and let $a\in G$. Prove the following:
- The right coset $Ka$ equals the set of values $b\in G$ such that $f(b)=f(a)$, or symbolically we have $$Ka = \{b\in G\mid f(b)=f(a)\} = f^{-1}(f(a)).$$
- The left coset $aK$ equals the same set $\{b\in G\mid f(b)=f(a)\}$, which means the left and right cosets are the same or $Ka=aK$.
In the previous problem, we saw that any time $K$ is the kernel of a homomorphism, we can talk about left or right cosets and obtain the exact same result, namely $Ka=aK$ for every $a\in G$. Any time a subgroup of $G$ satisfies this result, we'd like to have a special name for that subgroup. We call these subgroups normal.
Definition (Normal Subgroup $N\trianglelefteq G$)
We say that a subgroup $N$ of $G$ is a normal subgroup of $G$ if for each $a\in G$ the right coset $Na$ and left coset $aN$ are equal, so we have $Na=aN$ for every $a\in G$. We write $N\trianglelefteq G$ to mean that $N$ is a normal subgroup of $G$.
Before we can move too much farther, we need to prove some additional properties about cosets. We have already shown the following for a subgroup $H$ of the group $G$ with $a,b\in G$:
- We know $a\in Ha$.
- We know $Ha=H$ if and only if $a\in H$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
Let's add to this list of properties.
Problem 84 (Properties Of Cosets Part Two)
Let $H$ be a subgroup of $G$. Let $a,b\in G$. Prove the following facts about cosets.
- We have $Ha=Hb$ if and only if $ab^{-1}\in H$.
- We must have $Ha=Hb$ or $Ha\cap Hb=\emptyset$.
- We have $Ha=aH$ if and only if $aHa^{-1}=H$.
We've already seen all of these properties before when studying modular arithmetic. Let $G=\mathbb{Z}$ and let $H=n\mathbb{Z}$ for some $n\in\mathbb{N}$. The cosets of $H$ are $r+n\mathbb{Z}$ for $0\leq r<n$.
- The first property above states that $a+n\mathbb{Z}=b+n\mathbb{Z}$ if and only if $a-b\in n\mathbb{Z}$. Wait, this just says two numbers have the same remainder if and only if their difference is a multiple of $n$.
- The second property above states that either $a$ and $b$ have the same remainder, or they don't. It basically states that remainders are unique.
- The third property is trivial for $\mathbb{Z}$ because $\mathbb{Z}$ is an Abelian group and we always know $a+n\mathbb{Z}=n\mathbb{Z}+a$.
We've seen when creating identification graphs that if $Ha=aH$ for each $a\in G$, then the identification graph has a single arrow of each color leaving each coset. This suggests that the corresponding graph is the Cayley graph of a group. What we'd like to do is show that we can indeed create a group out of the cosets when $Ha=aH$ for every $a\in G$. When $Ha\neq aH$, then we've seen that the identification graph has several arrows of each color leaving each coset (either right or left).
The next problem has you show that if $Na=aN$ for every $a\in G$, i.e. we know $N$ is a normal subgroup of $G$, then the pattern we've seen of one arrow of each color leaving $Na$ is a general pattern that always holds
Problem (Identification Graphs Using Normal Subgroups Are Cayley Graphs)
Let $G$ be a group and suppose that $N$ is a normal subgroup of $G$. Let $a,b\in G$ and suppose that $ba\in Nc$, meaning we have an arrow from $Na$ to $Nc$ that is colored by $b$.
- Why does $Nc=N(ba)=(ba)N$? This should follow immediately from the properties of cosets and definition of normal. Be prepared to explain.
- Prove that if $x\in Na$, then $bx\in Nc$. (This shows that following arrow $b$ from anything in $Na$ will get you an element in $Nc$.)
- Extend your result to prove that if $y\in Nb$, then we also have $yx\in Nc$.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute as we may not have $na\neq an$, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1yn_2x$, then you should be able to write this, after some work, in either the form $n_3yx$ or the form $yxn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
The problem above suggests that we could take a coset $Ha$ and multiply it by a coset $Hb$ and obtain a coset $Hc$. This would suggest that we have a way of multiplying sets together. Let's give a formal definition of a set product.
Definition (The set product $HK$)
Suppose that $H$ and $K$ are nonempty subsets of a group $G$. Then we define the set product $HK$ to be the set $$HK=\{hk\mid h\in H, k\in K\}.$$ This is a binary operation on the collection of all nonempty subsets of $G$.
Problem (Practice With Set Products)
Let $G$ be the group of automorphisms of the square, i.e. the dihedral group of order 8. Let $K=\{(),(1,4)(2.3)\}$, $L=\{(),(1,3)(2,4)\}$, and $M=\{(),(1,3)\}$.
- Compute the set products $KL$ and $LK$, and then $KM$ and $MK$, and then $LM$ and $ML$. For which products does $AB=BA$?
- Let $K=\{(),(1,4)(2,3)\}$ as before. Let $\alpha = (1,2)(3,4)$ and $\beta = (1,2,3,4)$. Consider the right cosets $A=K\alpha$ and $B=K\beta$. Is the set product $AB$ another right coset of $K$? Does $Ka=aK$ for each $a\in G$?
- Let $L=\{(),(1,3)(2,4)\}$ as before. Consider the right cosets $C=L\alpha$ and $D=L\beta$. Is the set product $CD$ another right coset of $L$? Does $La=aL$ for each $a\in G$?
- Let $M=\{(),(1,3)\}$ as before. Consider the right cosets $A=M\alpha$ and $B=M\beta$. Is the set product $AB$ another right coset of $M$? Does $Ma=aM$ for each $a\in G$?
Feel free to use the Cayley table on page 31, or the Cayley graph below, to do your computations.
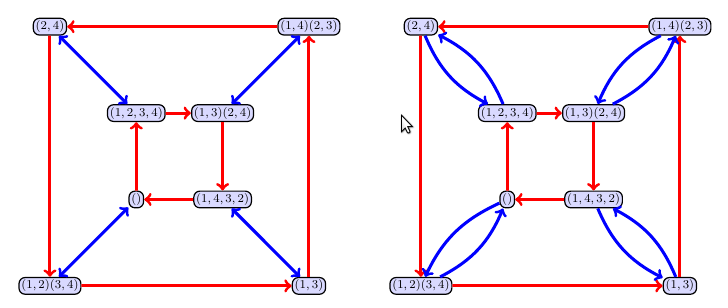
Click to see a partial solution.
To compute $KL$, you just have to compute $$\begin{align} KL &= \{()\circ (), ()\circ (1,3)(2,4), (1,4)(2,3)\circ (), (1,4)(2,3)\circ (1,3)(2,4)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ Similarly we just repeat the above in the reverse order to get $$\begin{align} LK &= \{()\circ (), ()\circ (1,4)(2,3), (1,3)(2,4)\circ (), (1,3)(2,4)\circ (1,4)(2,3)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ This shows that $KL=LK$.
Repeat this for $KM$ and $MK$, and you should see that these two sets are not the same. In particular, one contains $(1,2,3,4)$ and the other contains $(1,4,3,2)$. When you do the computations for $LM$ and $ML$, you should find that $LM=ML$. If you noticed that $L$ consists of the identity and the 180 degree rotation, both of which commute with every element, this can make lots of your work really quickly when working with $L$. Any time you work with elements in the center of a group, set products are much simpler to work with.
Now we move on to the problems involving $\alpha$ and $\beta$. Direct computation gives $$\begin{align} K\alpha &= \{(1,2)(3,4), (1,4)(2,3)\circ (1,2)(3,4)\}=\{(1,2)(3,4),(1,3)(2,4)\}, \text{ and }\\ K\beta &= \{(1,2,3,4), (1,4)(2,3)\circ (1,2,3,4)\}=\{(1,2)(3,4),(1,3)\}.\\ \end{align}$$ We then compute the set product to be $$\begin{align} (K\alpha)(K\beta) &=\{(1,2)(3,4),(1,3)(2,4)\}\{(1,2)(3,4),(1,3)\}\\ &=\{(1,2)(3,4)\circ(1,2)(3,4),(1,2)(3,4)\circ(1,3),(1,3)(2,4)\circ(1,2)(3,4),(1,3)(2,4)\circ(1,3)\}\\ &=\{(2,4),(1,4,3,2),(1,4,3,2),(2,4)\}\\ &=\{(2,4),(1,4,3,2)\}.\\ \end{align}$$ This is precisely the coset $K(2,4)$, so we do have that $(K\alpha)(K\beta)$ is a coset. If you want to know even more, notice that $\alpha\circ \beta = (2.4)$, so we see that $(K\alpha)(K\beta)=K(\alpha\beta)$. To answer the question, "Does $Ka=aK$ for every $a\in G$, we just have to look at the 4 different right cosets of $K$ and compare them to the 4 different left cosets of $K$. Direct computation shows that $K\beta = \{(1,2,3,4),(1,3)\}$, whereas $\beta K = \{(1,2,3,4),(2,4)\}.$ This shows that $K$ is not normal.
If you repeat these computations with $L$, you should find that $(L\alpha)(L\beta)=L(\alpha\beta)$, and that $La=aL$ for every $a\in G$. If you recall that the rotation $R_{180}=(1,3)(2,4)$ is an element that commutes with every other element, then this part of the problem is really fast.
For the last part, you should find that $M\alpha=M\beta=\{\alpha, \beta\}$, but when you compute $(M\alpha)(M\beta)$, you obtain a set with 4 elements, namely $\{\alpha^2=(),\beta^2, \alpha\beta, \beta\alpha\}$. Since $\alpha\beta\neq \beta \alpha$, and $\beta^2$ does not equal any of the other elements, this set product consists of 4 elements. Because $|M|=2$, the set product $(M\alpha)(M\beta)$ cannot be a coset of $M$. This is because any coset of $M$ would have to have 2 elements as well, one of the properties of cosets.
This next problem has you show that if $H$ is normal subgroup, then the set product produces a binary operation on cosets of $H$.
Problem 85 (The Set Product Is A Binary Operation On Cosets Of Normal Subgroups)
Suppose that $N$ is a normal subgroup of $G$. Let $a,b\in G$, and consider the two cosets $Na$ and $Nb$. Show that the set product $(Na)(Nb)$ is again a coset of $N$, and that we have $(Na)(Nb)=N(ab)$.
This shows that the set product is a binary operation on right cosets (and left cosets) of a normal subgroup $N$.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1an_2b$, then you should be able to write this, after some work, in either the form $n_3ab$ or the form $abn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute as we may not have $na\neq an$, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1an_2b$, then you should be able to write this, after some work, in either the form $n_3ab$ or the form $abn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
November 15
You can either jump straight into these problems, or revisit problems 3,4, and 6 from Wednesday. If you are stuck on Wednesday's, then instead please just start on the problems below, and then go back to Wednesday's (they're in the open problem list now). The problems below are specific examples of the ideas you are asked to prove on Wednesday's work.
Many of you need to revisit part 2 of problem 3 from Wednesday. You needed to show that either $Ha\cap Hb=\emptyset$ or $Ha=Hb$. THere are two cases. Either we have $Ha\cap Hb=\emptyset$ or we have $Ha\cap Hb\neq\emptyset$. In the second case you have to prove that $Ha=Hb$. This problem is equivalent to proving "If $Ha\cap Hb\neq \emptyset$ then $Ha=Hb$." I have a feeling that many of you can prove the latter, but your logical structure for proving an "Either/Or" statement is off (there are two cases). Please take a look at this problem again.
The problems below are very computational in nature. They ask you to repeatedly look at subgroups, cosets, identification graphs, and analyzing the relationship between them. The goal of doing these problems is to look for patterns, not blindly do hundreds of computations. So as you do these problems, ask yourself what general patterns you see. When you see the general pattern, describe it. Make conjectures. These conjectures are crucial to understanding. When you have made the conjecture yourself, you're more motivated to take the time to prove that your conjecture is true.
If you see the general pattern on the problems below, state the pattern. Then try to state a generalized version of the pattern you see. Most of mathematics is built because someone took the time to carefully study a single example in excruciating detail, extract the key principle from that problem, and then abstract the idea into an abstract setting that applies the principle in thousands of other places.
Problem (Practice With Homomorphisms from $\mathbb{Z}_n$ to $\mathbb{Z}_d$)
Let $G=\mathbb{Z}_{12}$ and $H=\mathbb{Z}_3$. Consider the map $f:G\to H$ defined by $f(x)=x\mod 3$.
- Show that $f$ is a homomorphism. What is the kernel $K$ of $f$.
- Draw Cayley graphs of $G$ and $H$ using the generating set $S=\{1\}$ in both cases, and then draw the identification graph of $G$ using right (or left) cosets of $K$.
- How many elements are in $G$, $H$, and $K$? What relationship is there between these?
- Repeat parts 1-3 if you use $H=\mathbb{Z}_2$ with $f(x)=x\mod 2$.
- Repeat parts 1-3 if you use $H=\mathbb{Z}_4$ with $f(x)=x\mod 4$.
- Repeat parts 1-3 if you use $H=\mathbb{Z}_6$ with $f(x)=x\mod 6$.
- Pick a positive integer $n$ and a divisor $d$ of $n$. Then repeat 1-3 if $G=\mathbb{Z}_n$, $H=\mathbb{Z}_d$, and $f$ is defined by $f(x)=x\mod d$.
You're welcome to stop when you see a general pattern, provided you describe the general pattern if $G=\mathbb{Z}_{n}$ and $H=\mathbb{Z}_d$.
Problem (Problem.Practice With Identification Graphs Of $\mathbb{Z}$)
Let $G=\mathbb{Z}$ and consider the subgroup $N=3\mathbb{Z}$.
- There are infinitely many possible ways to write cosets of $N$, namely we have $0+3\mathbb{Z}$, $1+3\mathbb{Z}$, $2+3\mathbb{Z}$, $3+3\mathbb{Z}$, $4+3\mathbb{Z}$, etc. Show that there are finitely many different cosets.
- Draw Cayley graphs of $G$ using the generating set $S=\{1\}$ in both cases, and then draw the identification graph of $G$ using right (or left) cosets of $N$. As there are only finitely many cosets, you should obtain a finite graph for the identification graph.
- Can you think of a group $H$ and a homomorphism $f:\mathbb{Z}\to H$ so that the kernel of $f$ is the subgroup $N=3\mathbb{Z}$? Hint: look at the previous problem.
- Repeat parts 1-3 if you use $H=\mathbb{Z}_5$ with $f(x)=x\mod 5$.
- Repeat parts 1-3 if you use $H=\mathbb{Z}_n$ with $f(x)=x\mod n$.
- What does this problem have to do with modular arithmetic?
Problem (Subgroups Cosets And Identification Graphs Of The Automorphisms Of The Square)
Let $G$ be the automorphism group of the square, so the dihedral group of order 8.
- Make a list of all the subgroups of $G$. You should have 1+5+3+1=10, namely 1 of order 1, 5 of order 2, 3 of order 4, and 1 of order 8. Think about the game "generate/don't generate" and build these subgroups by spanning elements of $G$.
- For each subgroup $H$, make a list of the right cosets of $H$. Then construct an identification graph of $G$ using the right cosets of $H$. What relationship is there between $|G|$, $|H|$, and the number of vertices in the identification graph?
- A Cayley graph has exactly one arrow of each color leaving each vertex. Some of your graphs above satisfy this property, and some have more than one arrow of each color leaving each vertex. Go through your list and decide which cannot be Cayley graphs and and which can be.
- Pick one of the graphs that is a Cayley graph (preferably not $H=\{e\}$ nor $H=G$). For that subgroup $H$, compute the right cosets of $H$.
- Pick one of the graphs that is not a Cayley graph. For that subgroup $H$, compute the right cosets of $H$.
- Is there a connection between left and right cosets and when identification graphs are Cayley graphs? What do you notice. Check if you are correct by looking at another subgroup of $H$.
Problem (Coset Products Of The Automorphisms Of The Square)
You'll need your work from the previous problem to continue with this problem.
- Pick a subgroup $H$ from the previous problem where the indentification graph of $G$ using right cosets of $H$ resulted in a Cayley graph. Compute the set products $(Ha)(Hb)$ for each pair of cosets. Organize your work into a multiplication table. Then repeat this with a different $H$.
- Pick a subgroup $H$ where the identification graph was not a Cayley graph. Compute the set products $(Ha)(Hb)$ for each pair of cosets. Organize your work into a multiplication table.
- Does the set product $(Ha)(Hb)$ always result in another coset of $H$? What did you find?
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
Please tell me which of these problems you are ready to present.
November 18
I'll add more connecting words between the problems later today, but here is the list of problems.
Last time we looked at the map $f:\mathbb{Z}_{12}\to \mathbb{Z}_3$ defined by $f(x)=x\pmod 3$ and showed that this was a homomorphism. Make sure you can prove the following exercise.
Exercise (A Homomorphism From $\mathbb{Z}_n$ to $\mathbb{Z}_d$ when $d$ is a divisor of $n$)
Consider the map $f:\mathbb{Z}_{n}\to \mathbb{Z}_d$ defined by $f(x)=x\pmod d$ where $d$ is a divisor of $n$. Show that $f$ is a homomorphism.
Click to see a solution
We need to show that $((x+y)\pmod n)\pmod d = (x\pmod d+y\pmod d)\pmod d$. We know that $a\pmod d=b\pmod d$ if and only if $a-b$ is a multiple of $d$ (does this look like the coset property that says $Ha=Hb$ if and only if $ab^{-1}\in H$?). We just need to show that $(x+y)\pmod n - (x\pmod d+y\pmod d)$ is a multiple of $d$. To do this, first note that using the division algorithm we can write $x\pmod d = x-q_xd$ and $y\pmod d = y-q_yd$ for some integers $q_x$ and $q_y$, and we can write $(x+y)\pmod n = (x+y)-qn$ for some integer $q$. Since we know $d$ is a divisor of $n$, we can also write $n=md$ for some integer $m$. We then compute $$\begin{align} (x+y)\pmod n - (x\pmod d+y\pmod d) &=(x+y-qn)-(x-q_xd)-(y-q_yd)\\ &=-qmd+q_xd+q_yd\\ &=d(q_x+q_y-qm), \end{align}$$ which is a multiple of $d$ as desired.
What happens if $d$ is not a divisor of $n$? Does the map $f:\mathbb{Z}_n\to \mathbb{Z}_d$ defined by $f(x)=x\mod d$ result in a homomorphism?
Problem 94 (When is $x \pmod d$ a homomorphism from $\mathbb{Z}_n$ to $\mathbb{Z}_d$)
Let $G=\mathbb{Z}_{12}$ and $H=\mathbb{Z}_5$. Let $f:G\to H$ be the map defined by $f(x)=x\mod 5$.
- Is the map $f:G\to H$ a homomorphism? Either prove that it is, or produce a counter example.
- Let $n$ be an integer and suppose that the positive integer $d<n$ is not a divisor of $n$. Is the map $f:\mathbb{Z}_n\to \mathbb{Z}_d$ defined by $f(x)=x\mod d$ a homomorphism?
The problems above also give us homomorphisms from $U(n)$ to $U(d)$, as the next problem shows. These maps are crucial in understanding cryptography.
Problem 95 (The set $U_d(n)$ and the homomorphism from $U(n)$ to $U(d)$)
For each integer $n\geq 2$ and each divisor $d$ of $n$, consider the map $f:U(n)\to U(d)$ defined by $f(x)=x\pmod d$.
- Show that this map is a homomorphism. [Hint: You will probably want to use the fact that $a\pmod k=b\pmod k$ if and only if $a-b$ is a multiple of $k$. This is the easiest way to prove statements about modular arithmetic. You have to show that two things are equal, namely that $((x\cdot y)\pmod n)\pmod d = ((x \pmod d)\cdot (y \pmod d))\pmod d$. You can remove the outermost $\pmod d$ by instead showing that the difference is a multiple of $d$.]
- Then explain why the set $U_d(n)=\{x\in U(n)\mid x\pmod d = 1\}$ is a subgroup of $U(n)$. (Hint: What is the kernel of $f$?)
- List the elements of $U_{5}(60)$.
The next theorem should come as no surprise. We've already shown that given any subgroup $H$ of $G$, that every element of $H$ is in one of the cosets of $H$. We've also shown that the cosets of $H$ are disjoint. These two facts to gether show that we can partition $G$ into a disjoint union of cosets of $H$. We also know that the size of each coset matches the order of $H$. So if we have $r$ disjoint cosets $Ha_1$, $Ha_2$, $Ha_3$, ..., $Ha_r$, all of which have the same number of elements, then we should be able to use this information to show that the order of $H$ divides the order of the group. This fact is called Lagranges theorem.
Problem 86 (Lagrange's Theorem Proof)
Prove Lagrange's Theorem.
Theorem (Lagrange's Theorem)
Suppose that $G$ is a finite group and that $H$ is a subgroup of $G$. Then the order of $H$ divides the order of $G$. In particular, we know that $|G|/|H|$ equals the number of distinct right (or left) cosets of $H$ in $G$.
We now have shown that the $|G|/|H|$ is precisely the number of cosets of $H$ there are in $G$. From a Cayley graph perspective, this is how many copies of $H$ are visible in the graph, as they are translated throughout the graph. The number of such cosets is called the index of $H$ in $G$, and written $|G:H|$.
Definition (Index of $H$ in $G$, or $|G:H|$)
If $H$ is a subgroup of $G$, then the index of $H$ in $G$, written $|G:H|$, is the number of distinct right (or left) cosets of $H$. Because of Lagrange's theorem, we know that $|G:H|=|G|/|H|$.
For the rest of today, we'll return to looking at when the left and right cosets of a subgroup agree, namely we'll be looking at normal subgroups.
Problem 87 (Some Normal Subgroups)
Prove the following facts.
- If $G$ is Abelian, then every subgroup of $G$ is normal.
- The center $Z(G)$ of any group $G$ is always a normal subgroup of $G$.
To prove many of the coset properties, we used the fact that $(Ha)b=H(ab)$. This looks a lot like an associative property. There's a bigger idea going on in the background than just the fact that $(Ha)b=H(ab)$. This is a set product of the form $(HA)B=H(AB)$ where the sets $A=\{a\}$ and $B=\{b\}$ consist of just one element. What if the sets $A$ and $B$ consist of more than one element. We would then have a binary operation on subsets of $G$ that is associative. This is precisely what it means to be a semigroup. The higher level idea is the concept of a semigroup.
Definition (Semigroup And Monoid)
Please look up the definitions of semigroup and monoid from Wikipedia.
We need the second property from the list below to proceed with group theory. The first property below should follow from the fact that $G$ is a group (why). The second property will require that you write down both sets in terms of their definitions, and then make some observations. The last property is for fun, skip it if you want.
Problem (The Collection Of Nonempty Subsets Of A Group Is A Monoid)
Let $G$ be a group, and consider the binary operation $HK$ on the collection $\mathscr{C}$ of nonempty subsets of $G$. Recall that $$HK=\{hk\mid h\in H, k\in K\}.$$ Prove the following:
- The set product $HK$ is indeed a binary operation on the collection $\mathscr{C}$ of nonempty subsets of $G$.
- The set product is associative, namely $(HK)L = H(KL)$. This proves that we have a semigroup.
- (Extra - We won't present this in class) The set $E=\{e\}$ is an identity element of $\mathscr{C}$, namely $EH=HE=H$ for any $H\in \mathscr{C}$. This proves that we have a monoid.
The key we need is that the set product is associative, which means that for any subgroup $H$, the coset product $(Ha)(Hb)$ is associative. Now if $N$ is a normal subgroup of $G$, then this means that the binary operation $(Na)(Nb)=N(ab)$ is an associative binary operation. These are two of the four things we need to obtain a group. We're now ready to prove that the collection of cosets of a normal subgroup is actually a group, and we call this the factor group of $G$ by $N$, or the quotient group of $G$ by $N$, and write $G/N$.
Definition (Factor Group or Quotient Group of $G$ by $N$, or $G/N$)
Let $G$ be a group. Let $N$ be a normal subgroup of $G$. Then we define the factor group of $G$ by $N$, or the quotient group of $G$ by $N$, to be the set $G/N = \{Na\mid a\in G\}$, i.e the collection of right cosets of $N$ using the set product $(Na)(Nb)=N(ab)$ as the binary operation.
Problem 88 (The Quotient Group $G/N$ Is A Group)
Let $G$ be a group and let $N$ be a normal subgroup of $G$. Prove that the set $G/N$ is actually a group under the operation of coset products.
November 20
Now that we have factor groups, we can take large groups and break them down into smaller groups which are easier to study. We'd like to reverse this process, namely start with some small groups and then combine them together to build larger groups. It would be nice if we could build all groups in this way. Then we could reduce our study of group theory to just understanding the simplest building blocks (called simple groups), and from those building blocks we could build every group. We will not fully obtain this goal this semester, but we're headed in that direction.
The first problem today helps you refresh your memory about the definitions of homomorphism and order of an element. You'll also need to use induction. The problem has you show that if $f$ is a homomorphism from $G$ to $H$, then while $f$ may not preserve the order of elements in $a$, it has to send an element of order $n$ to an element whose order divides $n$. This must happen on an element by element basis. So if we know something about the order of $f(a)$, then we know that $|a|$ must be a multiple of $|f(a)|$.
Problem 89 (The order of $a$ is a multiple of the order of $f(a)$, or $|a|=k|f(a)|$)
Suppose that $f:G\to H$ is a homomorphism. Prove that if $a\in G$ has order $n$, show that $|f(a)|$ divides $n$, i.e. show that $|a|$ is a multiple of $|f(a)|$.
In addition to homomorphisms interacting nicely with elements and orders, even more can be said. In particular, if you know that there are $n$ things that map to the indentity $e$ in the codomain, then the homomorphism must carry exactly $n$ elements from the domain to each element of the codomain. For this reason, we say that a homomorphism is an $n$-to-one map. If you look back at last week's problems, you should see somewhere that we showed a result very similar to this, namely when we showed that the kernel of $f$ is a normal subgroup. Please look back at that problem before tackling this one.
Problem 90 (A homomorphism is an $n$-to-one map)
Let $f:G\to H$ be a homomorphism.
- Suppose that $\ker f$ has order $n$. If we know that $f(g)=h$ for some $g\in G$, prove that there are exactly $n$ different elements in $G$ that map to $h$, so we know that the preimage of $h$, namely $f^{-1}(h)$, is a set with $n$ elements. This shows that $f$ is an $n$-to-one map.
- Prove that $f$ is injective if and only if the kernel of $f$ is trivial, i.e. $\ker f = \{e\}$.
- Prove that if $f$ is surjective and the kernel of $f$ is trivial, then $f$ is an isomorphism.
Here are some comment's about these problems.
- This should follow without any additional work from a previous problem. Just figure out which problem.
- This is why in linear algebra we know that $A\vec x = b$ has a single solution if and only if the only solution to $A\vec x=\vec 0$ is $\vec x= 0$, which means the columns of $A$ are linearly independent. Finding the kernel, or null space, is crucial in linear algebra.
- This is why in linear algebra we know that when the kernel of a square matrix is trivial, then the matrix is invertible.
We now know that a homomorphism is an $n$-to-one map. This fact is basically a directly result of the fact that the kernel of a homomorphism is normal. The next exercise shows that every normal subgroup is the kernel of some homomorphism. This shows that studying normal subgroups is precisely equivalent to studying kernels of homomorphisms. We've actually been using the result below without every stating it formally. Given a Cayley graph, we can easily build a map from the Cayley graph to the corresponding identification graph using right cosets of $N$ by sending $a$ to $Na$. This exercise just has you shows that this map is indeed a homomorphism whose kernel is $N$.
Exercise (A Subgroup Is Normal If And Only If It Is The Kernel Of Some Homomorphism)
Prove that $N$ is a normal subgroup of $G$ if and only if $N$ is the kernel of some homomorphism $f:G\to H$ from $G$ to another group $H$.
Click to see a solution.
We already know that if $N$ is the kernel of a homomorphism, then it is normal. So one direction of this if and only if proof is complete.
If we know $N$ is normal, then we can let $H=G/N$ and define $f:G\to H$ by $f(g)=Ng$. This map is a homomorphism because we already showed that $f(ab)=N(ab)=(Na)(Nb) = f(a)f(b)$ when we showed that the set product is a binary operation on cosets of a normal subgroup. The kernel of this map is the set of elements $g\in G$ such that $f(g)=N$. This is precise the set of $g\in G$ such that $Ng=N$ which is true if and only if $g\in N$ by the properties of cosets. Hence the kernel of this map is $N$.
This next problem has you practice using Lagrange's theorem. Both facts in the problem should follow immediately from applying Lagrange's theorem and another observation. These facts are often considered corollaries of Lagrange's theorem.
Problem 91 (The Order Of An Element Divides The Order Of A Group)
Let $G$ be a finite group. Use Lagrange's theorem to prove the following two corollaries.
- Let $a\in G$. The order of $a$ divides the order of $G$.
- If $|G|=p$ for some prime $p$, then $G$ is cyclic.
We are now ready to state and prove what mathematicians call the first isomorphism theorem. We've seen the following result several times before, without every fully stating it. When we consider the dihedral group of order 8 and let $N$ be the set of rotations, the identification graph looked a lot like $\mathbb{Z}_2$. The map $f:D_8\to \mathbb{Z}_2$ defined by $f(g)=0$ if $g$ is a rotation and $f(g)=1$ if $g$ is a flip, is a homomorphism from $D_8$ to $\mathbb{Z}_2$. The kernel of this homomorphism is precisely the rotations $N$. So the factor group $G/N$ consists of two cosets and is isomorphic to $\mathbb{Z}_2$. We now formally state the first isomorphism theorem.
Here's a formal statement of the first isomorphism theorem. It's slightly different than the text's, and we'll talk about why it's different in class. The version in the text involves more notation, but is essentially equivalent to this version. The key you need to proving this theorem comes from some of the earlier problems today (which problem has you show that something is an isomorphism?).
Problem 92 (The First Isomorphism Theorem Proof)
Prove the First Isomorphism Theorem.
Theorem (The First Isomorphism Theorem)
Let $f:G\to H$ be a surjective homomorphism with kernel $K$. Because we know that $f(x)=f(y)$ for any $y\in Kx$ (elements in the same coset of the kernel have the same image under $f$), then we can define a map $\phi:G/K\to H$ by defining $\phi(Kg)=f(g)$. This map $\phi$ is always an isomorphism.
We'll start using this theorem almost every day from here on out, as this is one of the biggest ideas in abstract algebra. For now, just make sure you can prove it.
Exercise (The Integers Under Addition Are Isomorphic To The Positive Integers Under Multiplication)
The set $\mathbb{R}^+$ is the set of positive real numbers. Consider the two groups $G=(\mathbb{R},+)$ and $H=(\mathbb{R}^{+},\cdot)$. Show that these two groups are isomorphic by showing that the exponential function $f(x)=\exp(x)$ is a group isomorphism.
Click to see a solution.
You could prove this by showing that the map is a homomorphism, and that it is a bijection by producing the inverse (namely $g(x)=\ln x$) and proving that it is an inverse. We've already done this in class.
Let's instead use the first isomorphism theorem. We know that $\exp(a+b)=\exp(a)\exp(b)$ high school algebra, so $f$ is a homomorphism. Given $y\in \mathbb{R}^{+}$, we let $x=\ln y$ and then $\exp(x)=y$, so the map is surjective. The only value such that $f(x)=1$ is $x=0$, so the kernel is $K=\ker f = \{0\}$. We could stop here and note that this means $f$ is 1 to 1, i.e. injective, and hence a bijection. Alternately, we could notice that $G/K=G$ (the identification graph of $G/K$ is the same as $G$ since $|K|=1$) and the first isomorphism theorem states that $f:G/K\to H$ is an isomorphism.
Now that we have discussed how to take a large group $G$ and create a factor group $G/N$, it's time to work this process in reverse. Let's start with two small groups $G$ and $H$, and from them create a larger group from them by using the Cartesian product $G\times H = \{(g,h)\mid g\in G, h\in H\}$. To turn this into a group, we'll just use the group operation independently on each component. What we need to do today is to show this actually gives a group, learn how to graph such a group, and then analyze how we find the order of an element $(g,h)$ in the product $G\times H$ if we know the orders of $g$ and $H$ in their respective groups. First, let's get a formal definition. Feel free to read along in chapter 8 of your text.
Definition (External Direct Products $G\times H$ or $G\oplus H$)
Suppose that $G$ and $H$ are both groups. The cartesian product $G\times H$ is the set $$G\times H = \{(g,h)\mid g\in G, h\in H\}.$$ The external product of $G$ and $H$ is this Cartesian product $G\times H$ together with the group operation $(g_1,h_1)\cdot(g_2,h_2)=(g_1g_2,h_1h_2)$. We'll use the notation $G\times H$ of $G\oplus H$ to talk about the external direct product of $G$ and $H$. We can also define the external direct product of $n$ groups. The definition is analagous, where instead of having two components, we now have $n$ components, and we multiply two elements of the external direct product by performing the product componentwise.
The first thing you should do is convince yourself that the external direct product is actually a group. This is a straightforward exercise that you should make sure you can do.
Exercise (The External Direct Product $G\oplus H$ is a Group of order $|G||H|$)
Prove that the external direct product $G\oplus H$ or $G\times H$ is a group. If both groups are finite, then show that the order of the external direct product is $|G||H|$.
Click to see a solution.
Let $G$ and $H$ be groups. The binary operation $(g,h)\times(a,b) = (ga,hb)$ is associative as we can compute $$((g,h)(a,b))(m,n)=(ga,hb)(m,n) = ((ga)m,(hb)n)$$ and similarly $$(g,h)((a,b)(m,n))=(g,h)(am,bn) = (g(am),h(bn)).$$ These two quantities are equal because the operation in both $G$ and $H$ is associative. The identity in $G\times H$ is simply $(e_g,e_H)$, and the inverse of $(g,h)$ is $(g^{-1},h^{-1})$. I'll let you show that these satisfy the requirements to be the identity and inverse.
If $G$ has order $|G|$ and $H$ has order $|H|$, and both are finite, then there are clearly $|G|$ choices for the first component, and $|H|$ choices for the second component. Hence the total number of elements in $G\times H$ is precisely $|G\times H|=|G||H|$.
Given a subgroup of $G$ and a subgroup of $H$, we can quickly create a subgroup of $G\times H$. This is what the next problem asks you to show. If you'd like a fun challenge, then prove that the converse of the following problem is true, or produce a counter example. Namely, if $C$ is a subgroup of $G\times H$, must it be true that $C=A\times B$ for some $A\leq G$ and $B\leq H$. First complete all the problems on this list, and then tackle this challenge.
Problem 72 (An External Direct Product Of Subgroups Is A Subgroup Of An External Direct Product)
Show that if $A$ is a subgroup of $G$ and $B$ is a subgroup of $H$, then $A\times B$ is subgroup of $G\times H$.
What does the Cayley graph of an external direct product look like? In particular if you know that $G$ and $H$ are both cyclic with generators $g$ and $h$, then what does the Cayley graph of $G\times H$ look like if we use the generators $(g,e_H)$ and $(e_G,h)$? The next problem has you draw several Cayley graphs of the product of cyclic groups.
Problem (Cayley Graphs Of External Direct Products Of Cyclic Groups)
Please complete the following: (Don't let the different notation $G\times H$ and $G\oplus H$ throw you off. They mean the exact same thing.)
- Draw the Cayley graph of $\mathbb{Z}_2\times\mathbb{Z}_2$ using the generating set $S=\{(1,0), (0,1)\}$.
- Draw the Cayley graph of $\mathbb{Z}_2\times\mathbb{Z}_3$ using the generating set $S=\{(1,0), (0,1)\}$.
- Draw the Cayley graph of $\mathbb{Z}_2\oplus\mathbb{Z}_5$ using the generating set $S=\{(1,0), (0,1)\}$.
- Draw the Cayley graph of $\mathbb{Z}_3\oplus\mathbb{Z}_5$ using the generating set $S=\{(1,0), (0,1)\}$.
- Draw the Cayley graph of $\mathbb{Z}_2\times\mathbb{Z}_3\times\mathbb{Z}_5$ using the generating set $S=\{(1,0,0), (0,1,0),(0,0,1)\}$.
- Draw the Cayley graph of $U(15)$ using the generating set $S=\{7,11\}$. Which graph above does this look like?
What patterns did you see above when constructing Cayley graphs? We'll discuss what you saw in class. The next exercise has you compute the orders of a few elements in some external direct products, as it prepares you to tackle the problem after.
Exercise (Practice With Orders In External Direct Products)
In each part below, you are given an element $(g,h)$ and a group $G\oplus H$. Compute the order of $g$ in $G$, the order of $h$ in $H$, and the order of $(g,h)\in G\oplus H$.
- $(1,2)\in \mathbb{Z}_2\times\mathbb{Z}_3$
- $(1,2)\in \mathbb{Z}_6\times\mathbb{Z}_4$
- $(1,2)\in \mathbb{Z}_6\times\mathbb{Z}_8$
- $(10,20)\in \mathbb{Z}_{4000}\times\mathbb{Z}_{600}$
Click to see a solution.
- We know $|1| = 2$ and $|2|=3$, and we can compute $(1,2)^k$ for each $k$ from $1$ to $6$ to obtain the sequence $((1,2),(0,1),(1,0),(0,2),(1,1),(0,0))$. This shows that $|(1,2)|=6$.
- We know $|1| = 6$ and $|2|=2$, and we can compute $(1,2)^k$ for each $k$ from $1$ to $6$ to obtain the sequence $((1,2),(2,0),(3,2),(4,0),(5,2),(0,0))$. This shows that $|(1,2)|=6$.
- We know $|1| = 6$ and $|2|=4$. Computing $(1,2)^k$ for each $k$ from $1$ to $12$ will show that the order is 12. Alternately, notice that in the product $(1,2)^k$, the first component will only equal 0 when $k$ is multiple of 6. Similarly, the second component will only be 0 when $k$ is a multiple of $4$. The number 12 is the smallest number for which both components will equal 0.
- We know $|10| = 400$ and $|20|=30$. In the product $(10,20)^k$, the first component will only equal 0 when $k$ is multiple of 400, and the second component will only be 0 when $k$ is a multiple of $30$. The least common multiple of 400 and 30 is 1200, which is the order of $(10, 20)$
Did you see in the exercise that the order of $(g,h)$ is the least common multiple of $|g|$ and $|h|$? The next problem has you prove this fact in general.
Problem 73 (The Order Of An Element In An External Direct Product Is The Least Common Multiple Of The Orders Of The Elements)
If $g\in G$ has order $n$ and $h\in H$ has order $m$, prove that the order of $(g,h)$ in $G\times H$ is the least common multiple of $n$ and $m$.
November 20
One of the reasons we care about factor groups is that we can often determine information about large, possibly hard to explore groups, by taking information from the factor group and pulling it back to the larger group. We know that the map $f:G\to G/N$ defined by $f(g)=Ng$ is a homomorphism, so we can often obtain information about $G$ by using this homomorphism to pull back information from $G/N$. The next problem has you show an example of this, namely that if you can find an element of order $k$ in $G/N$, then there must be an element of this order as well in $G$. Your work from last time should make this problem quite fast, provided you remember that $\langle a\rangle$ is a cyclic group, and as such is isomorphic to $\mathbb{Z}_{|a|}$, which we understand quite well.
Problem 93 (If A Factor Group $G/N$ Has An Element Of Order $k$ Then So Does $G$)
Suppose that $N$ is a normal subgroup of a finite group $G$ and that $Na$ has order $k$ as an element of $G/N$. Prove the following two facts.
- The order of $a$ in $G$ is a multiple of the order of $Na$ in $G/N$.
- There exists an element $b\in G$ that has order $k=|Na|$.
In other words, if a factor group has an element of order $k$, the the original group before factoring must have an element of order $k$ as well.
We have already shown that $Ha=aH$ for every $a\in G$ if and only if $aHa^{-1}=H$ for every $a\in G$. So one way to prove that a subgroup is normal is to prove that $aHa^{-1}=H$ for every $a\in G$. However, this requires that for each $a\in G$ you show both $aHa^{-1}\subseteq H$ and $H\subseteq aHa^{-1}$. The next problem simplifies this process even more. It says that if you know $aHa^{-1}\subseteq H$, then the other set inclusion must follow immediately.
Problem 94 (The Normal Subgroup Test)
Suppose that $G$ is a group and $H$ is a subgroup of $G$. Prove that $H$ is a normal subgroup of $G$ if and only if $xHx^{-1}\subseteq H$ for all $x\in G$.
How does normality behave when we look at subgroups? The following problem has you show that if you know $N$ is normal in $G$, and $N$ lies in some subgroup $B$ of $G$, then $N$ must be normal in $B$ as well. However, if we know $N$ is normal in $B$, and $B$ is normal in $G$, this does not guarantee that $N$ is normal in $G$. In symbols, we have $N\leq B\leq G$ and $N\trianglelefteq G$ implies $N\trianglelefteq B$, but we cannot say that $N\trianglelefteq B\trianglelefteq G$ implies $N\trianglelefteq G$. Being normal in a large group is enough to pass down to subgroups, but being normal in a subgroup is not enough to force normality in a larger group.
Problem 95 (Subgroups And Normality)
Suppose that $G$ is a group and that $A\leq B\leq G$.
- If $A$ is normal in $G$, prove that $A$ is normal in $B$.
- If $A$ is normal in $B$ and $B$ is normal in $G$, must $A$ be normal in $G$? Find a counter example to this.
The next problem has you show that when you compute factor groups, lots of properties pass immediately from $G$ to $G/N$. In particular, if $G$ is Abelian then $G/N$ is Abelian. Also, if $G$ is cyclic, then $G/N$ is cyclic. Many other properties follow as well.
Problem 96 (Factor Groups Preserve Being Cyclic And Abelian)
Suppose that $N$ is a normal subgroup of $G$.
- If $G$ is cyclic, prove that $G/N$ is cyclic.
- If $G$ is Abelian, prove that $G/N$ is Abelian.
The previous problem is an application of the bigger idea connected to homomorphism. Namely that the image of an Abelian group is Abelian, and the image of a cyclic group is cyclic.
Problem 97 (Images Of Abelian And Cyclic Groups)
Let $f:G\to H$ be a homomorphism. We have already shown that the image of $f$, written $f(G)$, is a subgroup of $H$.
- Prove that if $G$ is Abelian, then $f(G)$ is Abelian.
- Prove that if $G$ is cyclic, then $f(G)$ is cyclic.
How do the properties of Abelian and cyclic behave when combined with external direct products?
Problem 98 (External Direct Products Of Abelian And Cyclic Groups)
Suppose that $G$ and $H$ are groups.
- Prove or disprove: If both $G$ and $H$ are Abelian, then $G\oplus H$ is Abelian.
- Prove or disprove: If $G\oplus H$ is Abelian,then both $G$ and $H$ are Abelian.
- Prove or disprove: If both $G$ and $H$ are cyclic, then $G\oplus H$ is cyclic.
- Prove or disprove: If $G\oplus H$ is cyclic, then both $G$ and $H$ are cyclic.
The next problem has you prove Fermat's little lemma. We already conjectured this earlier in the semester when we noticed that if $p$ is a prime, then regardless of which $a$ we pick from $U(p)$, we must always have $a^{p-1}=1$. Sometimes, this is the order of $a$, whereas sometimes it is not. First, let's look at another conjecture we made earlier in the semester, to get us back into thinking about the $U$ groups.
Exercise (The Last Element Of UN Is Always Its Own Inverse)
Pick an integer $n$ greater than 1. Prove that $(n-1)\in U(n)$ is always its own multiplicative inverse.
Click to see a solution.
Notice that $(n-1)\pmod n = (-1)\pmod n$, which means $(n-1)^2\pmod n = (-1)^\pmod n = 1\pmod n$. This shows that the order of $n-1$ is 2, and also that $n-1$ is its own inverse.
Problem 99 (Fermat's Little Lemma)
Let $G$ be a finite group. Use Lagrange's theorem to prove the following two corollaries.
- We have $a^{|G|}=e$ for every $a\in G$.
- [Fermat's Little Lemma] Let $p$ be a prime and suppose $a\in U(p)$. Then we must have $a^p\pmod p=a$. (Hint: What is the order of $U(p)$?)
Using Fermat's little lemma and/or Lagrange's theorem, you should be able to rapidly prove the next result.
Exercise (The Order Of A In UP Divides P-1)
Let $p$ be a prime. Let $a\in U(p)$. Then $|a|$ divides $p-1$.
Click to see a solution.
There are several ways to prove this result.
- Since we know $a^p\pmod p = a$, we konw $a^{p-1}\pmod p = 1$. We know that $a^k=e$ in any group only when $k$ is a multiple of the order of $|a|$, so this means $k=p-1$ is a multiple of $|a|$.
- We now that $|U(p)|=p-1$. Hence every subgroup of $U(n)$, in particular $\left<a\right>$, must have an order that divides $p-1$. Since we know $|a|=|\left<a\right>|$, we know that $|a|$ divides $p-1$.
Because we are working with homomorphisms quite a bit in our work, we see the notation $f(g)=g$ quite a bit. We have also seen the notation $f^{-1}(h)$, but because homomomorphisms are not necessarily injective, this is not the inverse of $f$ applied to $h$. We have to remember that when we write $f^{-1}(h)$ we are talking about a set, namely the set of all $x\in G$ such that $f(x)=h$. We are not talking about a single $g$ so that $f(g)=h$. The notation $f^{-1}(h)$ represents the preimage (or inverse image) of $\{h\}$ under $f$. Here's a reminder of the formal definition.
Definition (Preimage Or Inverse Image)
If $f:A\to B$ and $C\subseteq B$, then the preimage of $C$ under $f$ is the set of all $a\in A$ such that $f(a)\in C$, and we write the preimage of $C$ under $f$ as $$f^{-1}(C)=\{a\in A\mid f(a)\in C\}.$$ When $C=\{c\}$ contains a single element, we often write the preimage of $C$ under $f$ as $f^{-1}(c)$ instead of using the more formal cumbersome notation $f^{-1}(\{c\})$.
Preimages and subgroups interact in a very nice way, namely homomorphisms preserve subgroups when computing inverse images. Next time we'll show that preimages preserve normality.
Problem 100 (The Preimage Of A Subgroup Under A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism. Let $B$ be a subgroup of $H$. Let $A$ be the preimage of $B$, namely $$A=f^{-1}(B)=\{g\in G\mid f(g)\in B\}.$$ Show that $A$ is a subgroup of $G$.
November 25
The next problem has you look at a very specific homomorphism from $G\times H$ to $G$. It's the start of a key idea that shows $(G\times H)/H\approx G$, namely that if you first create an external product, and then decide later to annihilate one of your factors, then you will obtain the other factor. It's basically an extension of the division fact from integers that says $(xy)/y=x$. A similar result shows that $(G\times H)/G\approx H$.
Problem (Collapsing A Factor Of An External Direct Product Yields The Other Factor, or $(G\times H)/H\approx G$)
Let $G$ and $H$ be groups, and consider the projection map $\pi_1:G\times H\to G$ defined by $\pi_1(g,h)=g$. We call this the projection map $\pi_1$ because it takes the element $(g,h)$ and returns the first component. The projection map $\pi_2$ would return the second component $h$.
- Prove that this projection map is a surjective homomorphism.
- What is the kernel of $\pi_1$, in other words what is $f^{-1}(e_G)$?
- Why is $(G\times H)/(\{e_G\}\times H)\approx G$?
- Show that $i_H:\{e_G\}\times H\to H$ defined by $i_H(e_G,h)=h$ is an isomorphism.
It's time to start using the power of factor groups, together with induction, to start proving some powerful theorems that apply to any finite group. The key to many of the problems we'll see in the next 4 weeks lies in the fact that the order of a factor group $G/N$ will always be less than the order of $G$, provided $N$ is not trivial. This means that if we use induction on the order of a group, then if we can use a factor group to pull back information to a larger group, induction will provide us with precisely the tool we need to prove some really powerful theorems about groups.
The first of these theorems is often called Cauchy's theorem. The more general version of Cauchy's theorem states that if $p$ is a prime that divides the order of the group, then $G$ must have an element of order $p$. The theorem below has you show this fact is true for Abelian groups. Because it's an Abelian group, every subgroup is normal, which means we can quickly create factor groups any time we obtain a subgroup. If we remove the Abelian condition, then we have to prove that a subgroup is normal before we can create a factor group. The Abelian condition is a simplifying assumption, which we will eventually remove.
Problem 106 (Abelian Groups Have An Element Of Order $p$ For Every Prime That Divides The Order Of The Group)
Let $G$ be an Abelian group and let $p$ be a prime. Prove that if $p$ divides the order of $G$, then there exists $a\in G$ with order $p$.
Hint: This problem is done by induction on the order of $G$.
For each integer $k\geq 2$, let $P(k)$ be the statement, "For every positive integer $n<k$, if $|G|=n$ and $p$ divides $|G|$ then $G$ has an element of order $p$." Use induction to prove that $P(k)$ is a true statement for every integer $k\geq 2$. This will require you to do two things.
- Is the statement $P(2)$ true? Is the statement $P(3)$ true?
- If you assume for some specific $k\geq 2$ that the statement $P(k)$ is true, then prove that the statement $P(k+1)$ is true. To prove $P(k+1)$ is a true statement, you have to prove that if $n<k+1$ and $|G|$ has order $n$ with $p$ dividing $G$, then $G$ has an element of order $p$. This is quite a lot of facts to prove. However, the induction assumption should prove every single one of them instantly except for when $n=k$. So you must show that if $|G|=k$ and $p$ divides $|G|$, then $G$ has an element of order $p$. You know for sure that $G$ has an element of some order other than 1, say $m=|a|$, which means that it has an element $b$ of some prime order $q$ (why?). If $q=p$ we're done. Otherwise, consider the factor group $G/\left<b\right>$. What is the order of $G/\left<b\right>$? Does $p$ divide $G/\left<b\right>$? What does the induction assumption then tell you? How does problem 103 help?
To tackle the next problem, you'll want to rely on the fact that $|(g,h)|=\text{lcm}(|g|,|h|)$, together with the fact that two integers are relatively prime if and only if their product is their least common multiple.
Problem 104 (A Direct Product Of Cyclic Groups Is Cyclic If And Only If The Groups Have Relatively Prime Orders)
Suppose that $G$ and $H$ are finite cyclic groups. Prove that $G\oplus H$ is cyclic if and only if $|G|$ and $|H|$ are relatively prime.
Exercise (A Direct Product Of Cyclic Groups Is Cyclic If And Only If The Groups Have Relatively Prime Orders)
Use induction to extend the previous result to the external direct product of $n$ cyclic groups. So prove that if $G_1,G_2,\ldots,G_n$ are $n$ cyclic groups, then $G_1\oplus G_2\oplus \cdots\oplus G_n$ is cyclic if and only if $|G_i|$ and $|G_j|$ are relatively prime when $i\neq j$.
Click to see a hint.
This exercise require that you use induction on an "if $p$ then $q$" statement. In addition, the $q$ part of the statement involves an if and only if. You must be very careful how you tackle this problem.
Problem 105 (An Isomorphism From $U(st)$ To $U(s)\oplus U(t)$ When $s$ And $t$ Are Relatively Prime)
Recall that $\varphi$, the Euler-phi function is defined by $\varphi(n)=|U(n)|$, the order of $U(n)$. Suppose $n=st$ where $s$ and $t$ are relatively prime. In this problem you'll show that $\varphi(st)=\varphi(s)\varphi(t)$.
- Show that $f:U(st)\to U(s)\oplus U(t)$ defined by $f(x)=(x\mod s,x\mod t)$ is an isomorphism.
- Why does $\varphi(st)=\varphi(s)\varphi(t)$ when $s$ and $t$ are relatively prime?
- Use the results above to compute $\varphi(17\cdot 19)$ and $\varphi(15\cdot 63)$.
Problem (Introduction To Internal Direct Products)
Consider the group $G\times H$. Let $A=G\times \{e_H\}$ and $B=\{e_G\}\times H$. Prove the following.
- $A\cap B$ contains only the identity element of $G\times H$.
- The set product $AB$ equals the whole group $G\times H$.
- $A$ and $B$ are normal subgroups of $G\times H$.
- $G\approx A$ and $H\approx B$, which means $G\times H=AB\cong A\times B$.
Did you notice what we did above. We started with a group created by using an external direct product. We then found two subgroup $A$ and $B$ of the group, and showed that the group was equal to the set product $AB$ (a product done internally in the group) and at the same time isomorphic to the external direct product $A\times B$. The first three conditions are the key.
Definition (Internal Direct Product Of Two Subgroups)
Suppose that $G$ is a group. If $H$ and $K$ are normal subgroups of $G$ such that $H\cap K=\{e\}$ and $HK=G$, then we say that $G$ is the internal direct product of $H$ and $K$.
Problem (When Is $HK$ A Subgroup Of $G$)
Suppose $H$ and $K$ are subgroups of $G$.
- Prove that $HK$ is a subgroup of $G$ if and only if $HK=KH$.
- Prove that if either $H$ or $K$ is normal in $G$, then $HK$ is a subgroup of $G$.
November 27
November 29
For more problems, see AllProblems
