Please Login to access more options.

Problem (Practice With Set Products)

This problem involves computing a bunch of set products. I'll provide partial solution below so you can check your work. The goal on this problem is to become comfortable wit computing set products. It will take some time. Spend 20 minutes on this problem. We'll spend more time in class tomorrow.

Let $G$ be the group of automorphisms of the square, i.e. the dihedral group of order 8. Let $K=\{(),(1,4)(2.3)\}$, $L=\{(),(1,3)(2,4)\}$, and $M=\{(),(1,3)\}$.

  1. Compute the set products $KL$ and $LK$, and then $KM$ and $MK$, and then $LM$ and $ML$. For which products does $AB=BA$?
  2. Let $K=\{(),(1,4)(2,3)\}$ as before. Let $\alpha = (1,2)(3,4)$ and $\beta = (1,2,3,4)$. Consider the right cosets $A=K\alpha$ and $B=K\beta$. Is the set product $AB$ another right coset of $K$? Does $Ka=aK$ for each $a\in G$?
  3. Let $L=\{(),(1,3)(2,4)\}$ as before. Consider the right cosets $C=L\alpha$ and $D=L\beta$. Is the set product $CD$ another right coset of $L$? Does $La=aL$ for each $a\in G$?
  4. Let $M=\{(),(1,3)\}$ as before. Consider the right cosets $A=M\alpha$ and $B=M\beta$. Is the set product $AB$ another right coset of $M$? Does $Ma=aM$ for each $a\in G$?

Feel free to use the Cayley table on page 31, or the Cayley graph below, to do your computations.

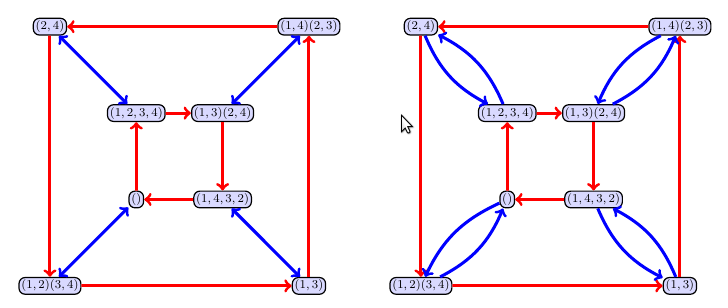
Click to see a partial solution.

To compute $KL$, you just have to compute $$\begin{align} KL &= \{()\circ (), ()\circ (1,3)(2,4), (1,4)(2,3)\circ (), (1,4)(2,3)\circ (1,3)(2,4)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ Similarly we just repeat the above in the reverse order to get $$\begin{align} LK &= \{()\circ (), ()\circ (1,4)(2,3), (1,3)(2,4)\circ (), (1,3)(2,4)\circ (1,4)(2,3)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ This shows that $KL=LK$.

Repeat this for $KM$ and $MK$, and you should see that these two sets are not the same. In particular, one contains $(1,2,3,4)$ and the other contains $(1,4,3,2)$. When you do the computations for $LM$ and $ML$, you should find that $LM=ML$. If you noticed that $L$ consists of the identity and the 180 degree rotation, both of which commute with every element, this can make lots of your work really quickly when working with $L$. Any time you work with elements in the center of a group, set products are much simpler to work with.

Now we move on to the problems involving $\alpha$ and $\beta$. Direct computation gives $$\begin{align} K\alpha &= \{(1,2)(3,4), (1,4)(2,3)\circ (1,2)(3,4)\}=\{(1,2)(3,4),(1,3)(2,4)\}, \text{ and }\\ K\beta &= \{(1,2,3,4), (1,4)(2,3)\circ (1,2,3,4)\}=\{(1,2)(3,4),(1,3)\}.\\ \end{align}$$ We then compute the set product to be $$\begin{align} (K\alpha)(K\beta) &=\{(1,2)(3,4),(1,3)(2,4)\}\{(1,2)(3,4),(1,3)\}\\ &=\{(1,2)(3,4)\circ(1,2)(3,4),(1,2)(3,4)\circ(1,3),(1,3)(2,4)\circ(1,2)(3,4),(1,3)(2,4)\circ(1,3)\}\\ &=\{(2,4),(1,4,3,2),(1,4,3,2),(2,4)\}\\ &=\{(2,4),(1,4,3,2)\}.\\ \end{align}$$ This is precisely the coset $K(2,4)$, so we do have that $(K\alpha)(K\beta)$ is a coset. If you want to know even more, notice that $\alpha\circ \beta = (2.4)$, so we see that $(K\alpha)(K\beta)=K(\alpha\beta)$. To answer the question, "Does $Ka=aK$ for every $a\in G$, we just have to look at the 4 different right cosets of $K$ and compare them to the 4 different left cosets of $K$. Direct computation shows that $K\beta = \{(1,2,3,4),(1,3)\}$, whereas $\beta K = \{(1,2,3,4),(2,4)\}.$ This shows that $K$ is not normal.

If you repeat these computations with $L$, you should find that $(L\alpha)(L\beta)=L(\alpha\beta)$, and that $La=aL$ for every $a\in G$. If you recall that the rotation $R_{180}=(1,3)(2,4)$ is an element that commutes with every other element, then this part of the problem is really fast.

For the last part, you should find that $M\alpha=M\beta=\{\alpha, \beta\}$, but when you compute $(M\alpha)(M\beta)$, you obtain a set with 4 elements, namely $\{\alpha^2=(),\beta^2, \alpha\beta, \beta\alpha\}$. Since $\alpha\beta\neq \beta \alpha$, and $\beta^2$ does not equal any of the other elements, this set product consists of 4 elements. Because $|M|=2$, the set product $(M\alpha)(M\beta)$ cannot be a coset of $M$. This is because any coset of $M$ would have to have 2 elements as well, one of the properties of cosets.

The following pages link to this page.