How Do You Build A Multiplication Table From A Cayley Graph

Please Login to access more options.

Problem (How Do You Build A Multiplication Table From A Cayley Graph)

Each of the Cayley graphs below is the Cayley graph of a group. However, the original labels on the vertices were lost, as well as the group operation table. However, from the Cayley graph alone we can reconstruct the group operation by constructing a multiplication table. We start by randomly choosing one point in the graph to be the identity $e$. There are two colors which we'll call $a$ and $b$. So if we start at $e$ and follow the arrow colored $a$, we should end at the group element $a$. Similarly, starting from $e$ and following the arrow colored $b$ gets us to the group element $b$. In both graphs below, starting at $e$ and following $a$ twice gets us to $c$, so we know that $a\cdot a=c$. If we start at any point $x$, then the product $ax$ means to start at $x$ and follow $a$. Because we know $c=a\cdot a$, then the product $cx=aax$ means start at $x$ and follow $a$ twice. Since we know $c=aae$ and $d=abe$ (start at $e$ and then follow $b$ then $a$), then the product $dc=abeaae$ which means start at $e$, then follow $a$ then $a$ then $b$ then $a$, which ends us at $b$. Use the Cayley graphs below to create the multiplication table for each group.

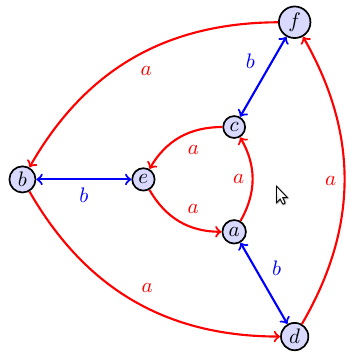
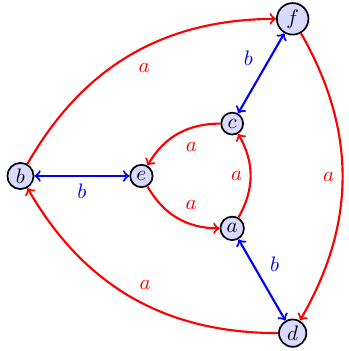
$$\begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&d&e&f&b\\ b & b& & & & &\\ c & c& & & &b&\\ d & d& & &b& &\\ f & f& & & & &\\ \end{array} \quad\quad\quad\quad\quad\quad\quad\quad\quad \begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a& & & & &\\ b & b& & & & &\\ c & c& & & & &\\ d & d& & & & &\\ f & f& & & & &\\ \end{array} $$

The following pages link to this page.