Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
The problems below are precisely the problems to work on for Monday. You should find that problem 5 is almost identical to problem 1 from Friday. You should also find that the problems involving subgroups and homomorphis are VERY close to the problems from Friday as well. On Monday, we'll go through most of the problems from Friday and Monday. The Cayley graph problems are there as exercises that you need to do so that you are comfortable with what a coset visually looks like in a group. Once we build a solid visual foundation, we can discuss abstract ideas and have a picture in our mind of what in the world we are talking about.
Thanks for your work today in class. I hope you had fun with identification graphs.
Today in class we'll have one person present each problem. You have 5-10 minutes to present your problem to a very small audience. Then we will review each problem as a class and discuss them. Here are the assignments.
| Presenter | Mini Audience/Helpers -Think of this as a group effort | ||
| Friday | Open 1.4 | Cassie | Joe |
| Friday | 1.1 | Bryce | Kinsey, Rob |
| Friday | 1.23 | Carla | Rich |
| Friday | 2.1 | Terry | Caley, Sam |
| Friday | 2.2 | Megan | Lilia |
| Friday | 3 | Nick | Tim |
| Monday | 1 | Li | Tara |
| Monday | 4 | Alexander | Brennan, Justin |
| Monday | 5 | Same as 1 From Friday | |
| Monday | 6 | Kimberly | Laura |
Problem 80 (When Does $H=Ha$)
Let $H$ be a nonempty subset of a group $G$. Prove that $H$ is a subgroup of $G$ if and only if $Ha=H$ for every $a\in H$.
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Problem (How Do You Build A Multiplication Table From A Cayley Graph)
Each of the Cayley graphs below is the Cayley graph of a group. However, the original labels on the vertices were lost, as well as the group operation table. However, from the Cayley graph alone we can reconstruct the group operation by constructing a multiplication table. We start by randomly choosing one point in the graph to be the identity $e$. There are two colors which we'll call $a$ and $b$. So if we start at $e$ and follow the arrow colored $a$, we should end at the group element $a$. Similarly, starting from $e$ and following the arrow colored $b$ gets us to the group element $b$. In both graphs below, starting at $e$ and following $a$ twice gets us to $c$, so we know that $a\cdot a=c$. If we start at any point $x$, then the product $ax$ means to start at $x$ and follow $a$. Because we know $c=a\cdot a$, then the product $cx=aax$ means start at $x$ and follow $a$ twice. Since we know $c=aae$ and $d=abe$ (start at $e$ and then follow $b$ then $a$), then the product $dc=abeaae$ which means start at $e$, then follow $a$ then $a$ then $b$ then $a$, which ends us at $b$. Use the Cayley graphs below to create the multiplication table for each group.
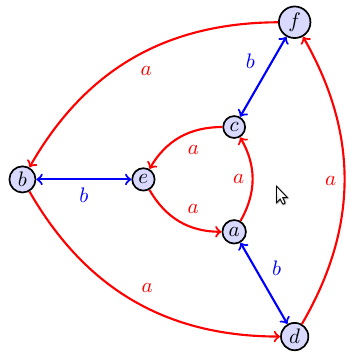
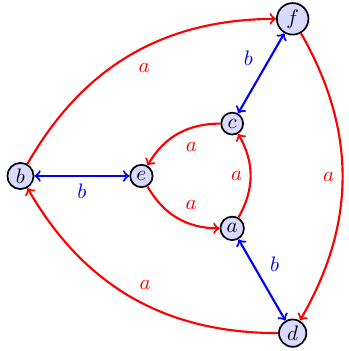
$$\begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&d&e&f&b\\ b & b& & & & &\\ c & c& & & &b&\\ d & d& & &b& &\\ f & f& & & & &\\ \end{array} \quad\quad\quad\quad\quad\quad\quad\quad\quad \begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a& & & & &\\ b & b& & & & &\\ c & c& & & & &\\ d & d& & & & &\\ f & f& & & & &\\ \end{array} $$
Click to see a solution. We won't have anyone present this one in class.
The correct Cayley tables are shown below. $$\begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&d&e&f&b\\ b & b&d&e&f&a&c\\ c & c&e&f&a&b&d\\ d & d&f&a&b&c&e\\ f & f&b&c&d&e&a\\ \end{array} \quad\quad\quad\quad\quad\quad\quad\quad\quad \begin{array}{c|cccccc} \cdot & e&a&b&c&d&f\\\hline e & e&a&b&c&d&f\\ a & a&c&f&e&b&d\\ b & b&d&e&f&a&c\\ c & c&e&d&a&f&b\\ d & d&f&c&b&e&a\\ f & f&b&a&d&c&e\\ \end{array} $$
Problem (Visualizing Cosets In A Cayley Graph)
The graph below is the Cayley graph of a group of order 12. A multiplication table for this group would consist of 144 entries. On this problem, we will visually construct the cosets of several subgroups of $G$ to illustrate how the cosets create a partition of $G$. Your goal is to understand visually the difference between right cosets $Hg$ and left cosets $gH$. You will need 4 colors to complete this problem.
- Let $H=\left<a\right> = \{e,a,a^2\}$. Compute all the right cosets $Hx$ of $H$ for $x\in G$. You should obtain 4 different right cosets. Use the graph below on your left and color the vertices so that two vertcies are colored the same if and only if they are in the same right coset. Then repeat this with the left cosets $gH$ of $H$, and color your vertices in the graph on the right.


- Now let $H=\left<b\right> = \{e,b\}$ and repeat part 1. Because $|H|=2$, you should obtain 6 cosets.


- Now let $H= \{e,b,i,k\}$ and repeat part 1. Because $|H|=4$, you should obtain 3 cosets.


- Now draw the 6 identification graphs obtained by considering either right cosets or left cosets for each of the subgroups above. You should notice that the only identification graph that is a Cayley graph is the last one where $H= \{e,b,i,k\}$. This happens precisely because the left and right cosets are the same, namely $gH=Hg$ for every $g\in G$. This is not a coincidence.
Let's now turn our attention back to homomorphisms. We'll see very soon that there is a big connection between homomorphisms and cosets. For today, let's just focus on some more properties of homomorphisms, namely that homomorphisms preserve subgroups. If you've forgotten the definition of the image of a set under a function, then here is a reminder.
Definition (Definition.The image of a function $f(A)$)
Let $f:G\to H$ be a function and let $A$ be subset of $G$. Recall that the image of $A$ under $f$ is the set $$f(A)=\{f(a)\mid a\in A\}.$$
If the set $A$ is a subgroup, then we would expect that a homomorphism maps the subgroup $A$ to a subgroup of $H$. This is precisely what the next problem asks you to show.
Problem 81 (The Image Of A Subgroup Under A Homomorphism Is A Subgroup)
Suppose that $f:G\to H$ is a homomorphism. Let $A$ be a subgroup of $G$. Show that $f(A)$ is a subgroup of $H$.
We now generalize some facts that we learned about the determinant map. We have already shown that the determinant map breaks up the set of possible matrices into equally sized cosets, where each coset consists of matrices of the same determinant. The next problem has you show that this property was not dependent on the determinant map, rather it has to do with the fact that the special linear group is a subgroup, and nothing more. You should find that your work on the problem The Set Product $Ha$ Preserves Determinants can almost be copied directly over to solve the next problem.
Problem 82 (Properties Of Cosets)
Let $G$ be a group, and let $H$ be a subgroup of $G$. Let $a,b \in G$. Prove the following:
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
As a last problem for today, let's generalize something we proved earlier in the semester. We've already shown that the intersection of two subgroups of a group is again a subgroup. What we'd like to show now is that the intersection of any collection of subgroups is again a subgroup of $G$. This fact is true whether the number of subgroups is finite, countable, or uncountable. If you do not remember the definition the intersection of a collection of subsets, here is a reminder.
Definition (Intersection Of A Collection Of Sets)
If $A$ and $B$ are a two sets, we say that $x\in A\cap B$ if and only if $x\in A$ and $x\in B$. If $\mathscr{B}$ is a collection of sets, then we say that $x$ is an element of the interesection of the collection of sets if and only if $x\in B$ for each $B\in \mathscr{B}$. We write this in set builder notation as $$\ds\bigcap_{B\in \mathscr{B}}B = \{x\mid x\in B \text{ for each }B\in \mathscr{B} \}.$$
Your proof to the problem Problem.TheIntersectionOfTwoSubgroups should provide you with a solution to this problem. You just need to change the fact that you are not working with two subgroups anymore, rather you are working with some nonempty collection of subgroups. You can find a solution to that problem on the key to the midterm, if you don't remember.
Problem (The Intersection Of Any Nonempty Collection Of Subgroups Is A Subgroup)
Let $G$ be a group. Suppose that we have a nonempty collection $\mathscr{B}$ of subgroups of $G$. Prove that the intersection of this collection of subgroups of $G$ is a subgroup of $G$. Symbolically, we can write this as $\ds\bigcap_{H\in \mathscr{B}}H$ is a subgroup of $G$.
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
For more problems, see AllProblems
