Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
Over the last few days we have been studying cosets quite a bit. We've seen that when we create an identification graph of $G$ using right cosets of $H$, we sometimes get a Cayley graph, and we sometimes don't. Today, we'll be focusing on the questions, "When is an identification graph of $G$ using cosets of $H$ another Cayley graph?" To answer this question, we'll need to explore the properties of cosets in depth.
- If $H$ is a subgroup of $G$ and $a\in H$, then $H\subseteq Ha$.
- If $Ha=H$ for every $a\in H$, then $H$ is a subgroup of $G$.
Problem 80 (When Does $H=Ha$)
Let $H$ be a nonempty subset of a group $G$. Prove that $H$ is a subgroup of $G$ if and only if $Ha=H$ for every $a\in H$.
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=bh$ for some $h\in H$).
Click if you want a hint.
If you assume $H$ is a subgroup, pick $a\in H$ and then prove that $H\subseteq Ha$ and $Ha\subseteq H$.
If you assume that $Ha=H$ for every $a\in H$, then you must prove $H$ is a subgroup. You'll need to rely on the fact that if $b,c\in H$, then we know $H=Hb$ and $H=Hc$ as sets. One of these should get you closure pretty quickly. If you let $b\in H$, then why does $H=Hb$ force the existence of $h\in H$ such that $b=hb$, and as such why does this mean $e\in H$. A similar argument should get you the fact that $b^{-1}\in H$ (as $e\in H$ forces $e=hb$ for some $h\in H$).
When working with the determinant map $f:GL(2,\mathbb{Z}_p)\to U(p)$, we have already shown that the kernel of this map is the special linear group $K=SL(2,\mathbb{Z}_p)$. We've also shown that the coset $Ka$ equals the set of all matrices whose determinant matches the determinant of $a$. Another way to say this is that $Ka$ equals the set of values $b\in G(2,\mathbb{Z}_p)$ such that $f(b)=f(a)$. A similar argument would show that $aK$ is the exact same set, which means we have $Ka=aK$. The next problem has you show that for any homomorphism $f:G\to H$ with kernel $K$, we always have $Ka=aK$ and that $Ka$ equals the set of $b\in G$ such that $f(b)=f(a)$.
Problem 83 (The Right And Left Cosets Of The Kernel Are Equal)
Suppose that $f:G\to H$ is a homomorphism. Let $K$ be the kernel of $f$ and let $a\in G$. Prove the following:
- The right coset $Ka$ equals the set of values $b\in G$ such that $f(b)=f(a)$, or symbolically we have $$Ka = \{b\in G\mid f(b)=f(a)\} = f^{-1}(f(a)).$$
- The left coset $aK$ equals the same set $\{b\in G\mid f(b)=f(a)\}$, which means the left and right cosets are the same or $Ka=aK$.
In the previous problem, we saw that any time $K$ is the kernel of a homomorphism, we can talk about left or right cosets and obtain the exact same result, namely $Ka=aK$ for every $a\in G$. Any time a subgroup of $G$ satisfies this result, we'd like to have a special name for that subgroup. We call these subgroups normal.
Definition (Normal Subgroup $N\trianglelefteq G$)
We say that a subgroup $N$ of $G$ is a normal subgroup of $G$ if for each $a\in G$ the right coset $Na$ and left coset $aN$ are equal, so we have $Na=aN$ for every $a\in G$. We write $N\trianglelefteq G$ to mean that $N$ is a normal subgroup of $G$.
Before we can move too much farther, we need to prove some additional properties about cosets. We have already shown the following for a subgroup $H$ of the group $G$ with $a,b\in G$:
- We know $a\in Ha$.
- We know $Ha=H$ if and only if $a\in H$.
- We know $b\in Ha$ if and only if $Hb=Ha$.
- The function $f:H\to Ha$ defined by $f(h)=ha$ is a bijection.
- We have $|H|=|Ha|$.
Let's add to this list of properties.
Problem 84 (Properties Of Cosets Part Two)
Let $H$ be a subgroup of $G$. Let $a,b\in G$. Prove the following facts about cosets.
- We have $Ha=Hb$ if and only if $ab^{-1}\in H$.
- We must have $Ha=Hb$ or $Ha\cap Hb=\emptyset$.
- We have $Ha=aH$ if and only if $aHa^{-1}=H$.
We've already seen all of these properties before when studying modular arithmetic. Let $G=\mathbb{Z}$ and let $H=n\mathbb{Z}$ for some $n\in\mathbb{N}$. The cosets of $H$ are $r+n\mathbb{Z}$ for $0\leq r<n$.
- The first property above states that $a+n\mathbb{Z}=b+n\mathbb{Z}$ if and only if $a-b\in n\mathbb{Z}$. Wait, this just says two numbers have the same remainder if and only if their difference is a multiple of $n$.
- The second property above states that either $a$ and $b$ have the same remainder, or they don't. It basically states that remainders are unique.
- The third property is trivial for $\mathbb{Z}$ because $\mathbb{Z}$ is an Abelian group and we always know $a+n\mathbb{Z}=n\mathbb{Z}+a$.
We've seen when creating identification graphs that if $Ha=aH$ for each $a\in G$, then the identification graph has a single arrow of each color leaving each coset. This suggests that the corresponding graph is the Cayley graph of a group. What we'd like to do is show that we can indeed create a group out of the cosets when $Ha=aH$ for every $a\in G$. When $Ha\neq aH$, then we've seen that the identification graph has several arrows of each color leaving each coset (either right or left).
The next problem has you show that if $Na=aN$ for every $a\in G$, i.e. we know $N$ is a normal subgroup of $G$, then the pattern we've seen of one arrow of each color leaving $Na$ is a general pattern that always holds
Problem (Identification Graphs Using Normal Subgroups Are Cayley Graphs)
Let $G$ be a group and suppose that $N$ is a normal subgroup of $G$. Let $a,b\in G$ and suppose that $ba\in Nc$, meaning we have an arrow from $Na$ to $Nc$ that is colored by $b$.
- Why does $Nc=N(ba)=(ba)N$? This should follow immediately from the properties of cosets and definition of normal. Be prepared to explain.
- Prove that if $x\in Na$, then $bx\in Nc$. (This shows that following arrow $b$ from anything in $Na$ will get you an element in $Nc$.)
- Extend your result to prove that if $y\in Nb$, then we also have $yx\in Nc$.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute as we may not have $na\neq an$, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1yn_2x$, then you should be able to write this, after some work, in either the form $n_3yx$ or the form $yxn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
The problem above suggests that we could take a coset $Ha$ and multiply it by a coset $Hb$ and obtain a coset $Hc$. This would suggest that we have a way of multiplying sets together. Let's give a formal definition of a set product.
Definition (The set product $HK$)
Suppose that $H$ and $K$ are nonempty subsets of a group $G$. Then we define the set product $HK$ to be the set $$HK=\{hk\mid h\in H, k\in K\}.$$ This is a binary operation on the collection of all nonempty subsets of $G$.
Problem (Practice With Set Products)
Let $G$ be the group of automorphisms of the square, i.e. the dihedral group of order 8. Let $K=\{(),(1,4)(2.3)\}$, $L=\{(),(1,3)(2,4)\}$, and $M=\{(),(1,3)\}$.
- Compute the set products $KL$ and $LK$, and then $KM$ and $MK$, and then $LM$ and $ML$. For which products does $AB=BA$?
- Let $K=\{(),(1,4)(2,3)\}$ as before. Let $\alpha = (1,2)(3,4)$ and $\beta = (1,2,3,4)$. Consider the right cosets $A=K\alpha$ and $B=K\beta$. Is the set product $AB$ another right coset of $K$? Does $Ka=aK$ for each $a\in G$?
- Let $L=\{(),(1,3)(2,4)\}$ as before. Consider the right cosets $C=L\alpha$ and $D=L\beta$. Is the set product $CD$ another right coset of $L$? Does $La=aL$ for each $a\in G$?
- Let $M=\{(),(1,3)\}$ as before. Consider the right cosets $A=M\alpha$ and $B=M\beta$. Is the set product $AB$ another right coset of $M$? Does $Ma=aM$ for each $a\in G$?
Feel free to use the Cayley table on page 31, or the Cayley graph below, to do your computations.
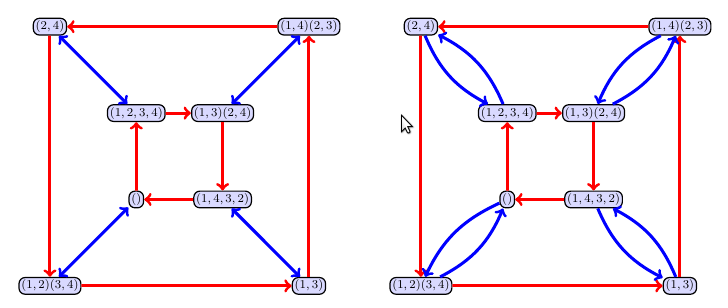
Click to see a partial solution.
To compute $KL$, you just have to compute $$\begin{align} KL &= \{()\circ (), ()\circ (1,3)(2,4), (1,4)(2,3)\circ (), (1,4)(2,3)\circ (1,3)(2,4)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ Similarly we just repeat the above in the reverse order to get $$\begin{align} LK &= \{()\circ (), ()\circ (1,4)(2,3), (1,3)(2,4)\circ (), (1,3)(2,4)\circ (1,4)(2,3)\} \\ &= \{(), (1,3)(2,4), (1,4)(2,3), (1,2)(3,4)\}. \end{align}.$$ This shows that $KL=LK$.
Repeat this for $KM$ and $MK$, and you should see that these two sets are not the same. In particular, one contains $(1,2,3,4)$ and the other contains $(1,4,3,2)$. When you do the computations for $LM$ and $ML$, you should find that $LM=ML$. If you noticed that $L$ consists of the identity and the 180 degree rotation, both of which commute with every element, this can make lots of your work really quickly when working with $L$. Any time you work with elements in the center of a group, set products are much simpler to work with.
Now we move on to the problems involving $\alpha$ and $\beta$. Direct computation gives $$\begin{align} K\alpha &= \{(1,2)(3,4), (1,4)(2,3)\circ (1,2)(3,4)\}=\{(1,2)(3,4),(1,3)(2,4)\}, \text{ and }\\ K\beta &= \{(1,2,3,4), (1,4)(2,3)\circ (1,2,3,4)\}=\{(1,2)(3,4),(1,3)\}.\\ \end{align}$$ We then compute the set product to be $$\begin{align} (K\alpha)(K\beta) &=\{(1,2)(3,4),(1,3)(2,4)\}\{(1,2)(3,4),(1,3)\}\\ &=\{(1,2)(3,4)\circ(1,2)(3,4),(1,2)(3,4)\circ(1,3),(1,3)(2,4)\circ(1,2)(3,4),(1,3)(2,4)\circ(1,3)\}\\ &=\{(2,4),(1,4,3,2),(1,4,3,2),(2,4)\}\\ &=\{(2,4),(1,4,3,2)\}.\\ \end{align}$$ This is precisely the coset $K(2,4)$, so we do have that $(K\alpha)(K\beta)$ is a coset. If you want to know even more, notice that $\alpha\circ \beta = (2.4)$, so we see that $(K\alpha)(K\beta)=K(\alpha\beta)$. To answer the question, "Does $Ka=aK$ for every $a\in G$, we just have to look at the 4 different right cosets of $K$ and compare them to the 4 different left cosets of $K$. Direct computation shows that $K\beta = \{(1,2,3,4),(1,3)\}$, whereas $\beta K = \{(1,2,3,4),(2,4)\}.$ This shows that $K$ is not normal.
If you repeat these computations with $L$, you should find that $(L\alpha)(L\beta)=L(\alpha\beta)$, and that $La=aL$ for every $a\in G$. If you recall that the rotation $R_{180}=(1,3)(2,4)$ is an element that commutes with every other element, then this part of the problem is really fast.
For the last part, you should find that $M\alpha=M\beta=\{\alpha, \beta\}$, but when you compute $(M\alpha)(M\beta)$, you obtain a set with 4 elements, namely $\{\alpha^2=(),\beta^2, \alpha\beta, \beta\alpha\}$. Since $\alpha\beta\neq \beta \alpha$, and $\beta^2$ does not equal any of the other elements, this set product consists of 4 elements. Because $|M|=2$, the set product $(M\alpha)(M\beta)$ cannot be a coset of $M$. This is because any coset of $M$ would have to have 2 elements as well, one of the properties of cosets.
This next problem has you show that if $H$ is normal subgroup, then the set product produces a binary operation on cosets of $H$.
Problem 85 (The Set Product Is A Binary Operation On Cosets Of Normal Subgroups)
Suppose that $N$ is a normal subgroup of $G$. Let $a,b\in G$, and consider the two cosets $Na$ and $Nb$. Show that the set product $(Na)(Nb)$ is again a coset of $N$, and that we have $(Na)(Nb)=N(ab)$.
This shows that the set product is a binary operation on right cosets (and left cosets) of a normal subgroup $N$.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1an_2b$, then you should be able to write this, after some work, in either the form $n_3ab$ or the form $abn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
Click if you want a hint.
You've got to make use of the fact that $Na=aN$ for every $a\in G$. So we have $Nb=bN$, $Nc=cN$, $Nx=xN$, etc. Why is this useful? Any time you see $na$ in your work for some $n\in N$, you know that $na\in Na$ which means $na\in aN$ which means there exists some $n'\in N$ with $na=an'$. You don't have the ability to commute as we may not have $na\neq an$, but we get ALMOST commutativity. We can write $na=an'$ for some different $n'\in N$. The $'$ symbol just means that it's a different element. It's not a derivative.
So in your work if you ever see $bn_1a$, you can instead either write $bn=n_2b$ or you could write $na=an_3$ for some $n_2,n_3\in N$, and then you have $bn_1a = n_2ba=ban_3$. Similarly, if you see $n_1an_2b$, then you should be able to write this, after some work, in either the form $n_3ab$ or the form $abn_4$ (you'll need to use the closure of the operation in $N$ to combine elements in $N$).
You can't use the commutative law, but you have something pretty close.
Problem (Continue Working On Open Problems)
Please look at the Open Problems list, and continue working on these. In your preparation, please tell me which of the problems on the list you would feel comfortable presenting to the class. When we have a critical mass of students ready to present each problems, we'll discuss it in class (sometimes with a presentation, sometimes with just a discussion).
For more problems, see AllProblems
