- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
This is Day 1 in Unit 2.
Prep
We're in Unit 2 - Derivatives. Your homework assignment each day is to spend 1-2 hours working on the next 4 tasks from the current unit's prep.
Brain Gains (Rapid Recall, Jivin' Generation)
- For the function $V = \pi r^2 h$, assume that both $r$ and $h$ depend on a parameter $t$. Then compute $\frac{dV}{dt}$ using implicit differentiation.
Solution
Using the chain rule, we compute $$\frac{dV}{dt} = \pi 2r \frac{dr}{dt}h+\pi r^2\frac{dh}{dt}.$$ Multiplying both sides by $dt$ gives the differential $$dV = 2\pi rh dr +\pi r^2dh = (2\pi rh,\pi r^2)\cdot(dr,dh).$$ The gradient of $V$, or total derivative of $V$, is the vector $\nabla V = (2\pi rh,\pi r^2)$. The partial derivatives of $V$ are the components $\frac{\partial V}{\partial r} = 2\pi r h$ and $\frac{\partial V}{\partial h} = \pi r^2$
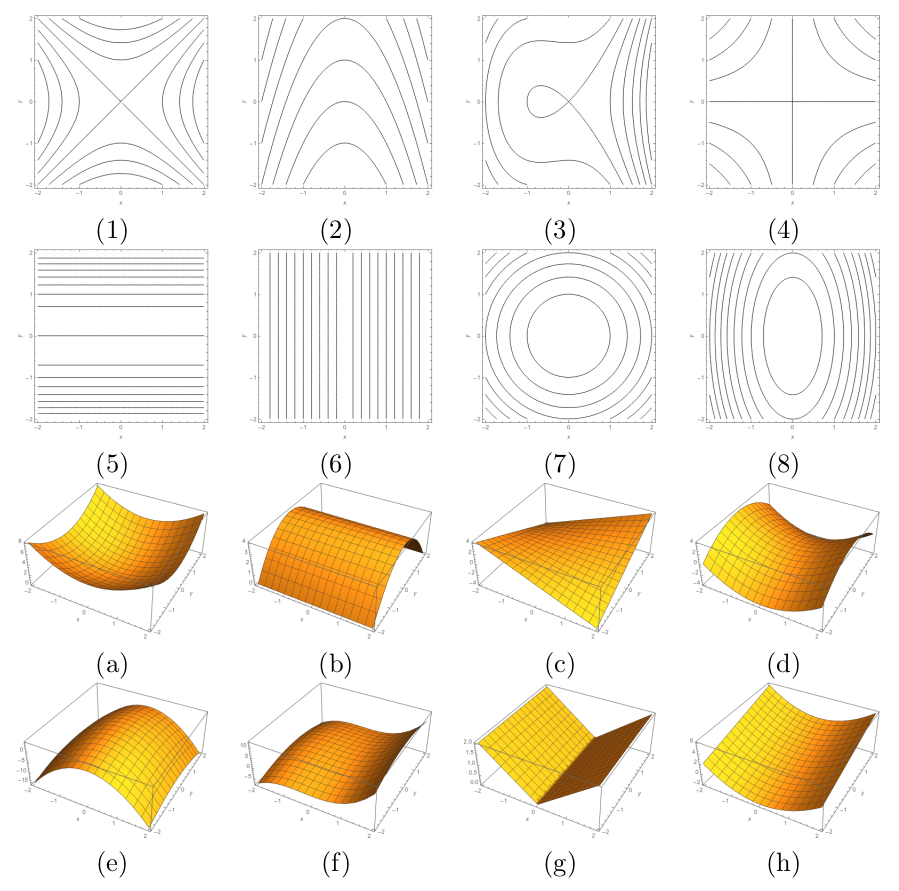
- Match the contour plots to the surface.
- For the function $f(x,y) = x^2-y^2$, graph the level curve that passes through the point $(1,0)$.
- Let $z= x^3+4xy$. We can think of this as an elevation function that tells us the height $z$ of a hill at a point $(x,y)$. Compute $dz$ in terms of $x$, $y$, $dx$, and $dy$.
Solution
Implicit differentiation gives $$\frac{dz}{dt} = 3x^2 \frac{dx}{dt} + (4x)\frac{dy}{dt}+(4\frac{dx}{dt})(y).$$ Multiplying by $dt$ gives the differential $$dz = 3x^2 dx + (4x)(dy)+(4dx)(y).$$
- Write your answer above in the form $dz = (?_1) dx+(?_2) dy$.
Solution
By collecting the terms with a $dx$ in them, and then the terms with a $dy$ in them, we obtain $$dz = (3x^2+4y)dx+(4x)dy.$$
- Write your answer above as the dot product of two vectors, namely $dz= (?????)\cdot (dx,dy)$.
Solution
From inspection, we obtain $$dz = (3x^2+4y,4x)\cdot (dx,dy).$$ You can check this is correct by performing the dot product above and comparing it to the previous problem. This problem is essentially pattern recognition, and trying to find two vectors that give the desired dot product.
- What is the gradient of $z$ for the function above, written $\vec \nabla z(x,y)$? We will often just write $\vec\nabla z$, when the input variables $x$ and $y$ are clear from context.
Solution
The gradient of $z$ is the vector $$\vec \nabla z = (3x^2+4y,4x).$$ Just strip the vector of differentials $(dx,dy)$ off of $dz$. This means we always have $$dz = \vec \nabla z\cdot (dx,dy).$$
In first semester calculus, we had $dy = f' dx$. The gradient $\vec \nabla z$ is the generalization of the derivative to higher dimensions. Note that the gradient here has two parts, which we call partial derivatives.
- What is the partial derivative of $z$ with respect to $x$, written $\ds\frac{\partial z}{\partial x}$ or $z_x$ or $D_x z$?
Solution
The partial derivative of $z$ with respect to $x$ is the quantity $$\frac{\partial z}{\partial x} = 3x^2+4y.$$ This is the slope $\frac{dz}{dx}$ if you let $dy=0$ in $dz = (3x^2+4y)dx+(4x)dy.$ It represents the slope of the function if you change $x$ but hold $y$ constant (hence $dy=0$). We use a stylized "d" (written $\partial$ in $\frac{\partial z}{\partial x}$) to help us remember that just $x$ is changing. The subscript notation can be used (so $z_x$) when no ambiguity arises from other subscripts.
- What is the partial derivative of $z$ with respect to $y$, written $\ds\frac{\partial z}{\partial y}$ or $z_y$ or $D_y z$?
Solution
The partial derivative of $z$ with respect to $y$ is the quantity $$\frac{\partial z}{\partial x} = 4x.$$ This is the slope $\frac{dz}{dx}$ if you let $dy=0$ in $dz = (3x^2+4y)dx+(4x)dy.$ It represents the slope of the function if you change $y$ but hold $x$ constant (hence $dx=0$). We use a stylized "d" (written $\partial$ in $\frac{\partial z}{\partial y}$) to help us remember that just $y$ is changing. The subscript notation can be used (so $z_y$) when no ambiguity arises from other subscripts.
Group Problems
- For the function $z = x^2y+y^2$, compute $\frac{dz}{dt}$ (assuming that both $x$ and $y$ depend on the parameter $t$).
- A rover is located on a hill whose elevation is given by $z=f(x,y) = 3x^2+2xy+4y^2$.
- Compute the differential $dz$ in terms of $x$, $y$, $dx$, and $dy$, and write it in the form $dz=(?_1)dx+(?_2)dy.$
- Write your answer above as the dot product of two vectors, i.e., $dz = (??, ??)\cdot(dx, dy).$
- State the gradient of $f$, so $\vec \nabla f$.
- State $\dfrac{\partial f}{\partial x}$ and $f_y$.
- The sides of a rectangle $x=3$ ft and $y=2$ ft, with tolerances $dx = .1$ ft and $dy = 0.05$ ft. Use differentials to estimate the tolerance on the area $A=xy$ that results from the given tolerances on $x$ and $y$. So compute $dA$ and then plug in $x$, $y$, $dx$, $dy$, as given. [Check: $dA = 0.35.$]
- Let $z = f(x,y) = x^2+y^2$.
- Construct a 2D contour plot. (Let $z = 1$, and plot the resulting curve. Then let $z=4$ and plot the resulting curve. Repeat with various values for the output $z$.)
- Construct a 3D surface plot.
- Compute the gradient of $f$.
- Note that the gradient of $f$ is a vector field. Graph the vector field on the same 2D plot as you did your contour plot.
- Let $z = f(x,y) = 4-y^2$.
- Construct a 2D contour plot.
- Construct a 3D surface plot.
- Compute the gradient of $f$.
- Note that the gradient of $f$ is a vector field. Graph the vector field on the same 2D plot as you did your contour plot.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
