- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
This is day 8 of Unit 10. We'll have two more class periods, and then a quiz on this unit.
Brain Gains (Rapid Recall, Jivin' Generation)
- Find the area of the parallelogram whose edges are the vector $(1,2,3)$ and $(-2,0,1)$. Then find the volume of the parallelepiped whose edges are the vectors $(1,2,3)$, $(-2,0,1)$, and $(-1,-1,2)$.
Solution
The area is $|(1,2,3)\times(-2,0,1)|=\sqrt{69}$, and the volume is $|[(1,2,3)\times (-2,0,1)]\cdot (-1,-1,2)|=13$.
Cross[{1, 2, 3}, {-2, 0, 1}] // Norm
Dot[Cross[{1, 2, 3}, {-2, 0, 1}], {-1, -1, 2}]
Parallelepiped[{0, 0, 0}, {{1, 2, 3}, {-2, 0, 1}, {-1, -1, 2}}] // Graphics3D
- Compute the Jacobian $\dfrac{\partial(x,y,z)}{\partial(r,\theta,z)}$ for cylindrical coordinates $x=r\cos\theta$, $y=r\sin\theta$, $z=z$.
Solution
This is part the prep tasks. The differential of the change of coordinates is $$ \begin{pmatrix}dx\\dy\\dy\end{pmatrix} =\begin{pmatrix}\cos\theta\\\sin\theta\\0\end{pmatrix} dr +\begin{pmatrix}-r\sin\theta\\r\cos\theta\\0\end{pmatrix} d\theta +\begin{pmatrix}0\\0\\1\end{pmatrix} dz. $$ We need to form the triple product of these 3 vectors. The cross product of the first two vectors is $(0,0,r)$. The dot product of this with $(0,0,1)$ yields $r$, which means $$\dfrac{\partial(x,y,z)}{\partial(r,\theta,z)} = |r|.$$ As such, we can replace $dV$ with $|r|dz dr d\theta$ in integrals that use cylindrical coordinates.
With Mathematica (and knowing that the determinant of a 3 by 3 matrix computes the triple product), we can perform all the computations above quite quickly. The middle line below just shows the derivative (whose columns are the partial derivatives computed above).
coordinates = {r Cos[theta], r Sin[theta], z};
D[coordinates, {{r, theta, z}}] // MatrixForm
jacobian = D[coordinates, {{r, theta, z}}] // Det // Abs // Simplify
Because I had to type {r, theta, z} twice, I created an alternate version that stores this as a variable.
variables = {r, theta, z}
coordinates = {r Cos[theta], r Sin[theta], z};
D[coordinates, {variables}] // MatrixForm
jacobian = D[coordinates, {variables}] // Det // Abs // Simplify
Now we can compute the Jacobian for spherical coordinates quite quickly.
variables = {rho, phi, theta}
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]};
D[coordinates, {variables}] // MatrixForm
jacobian = D[coordinates, {variables}] // Det // Abs // Simplify
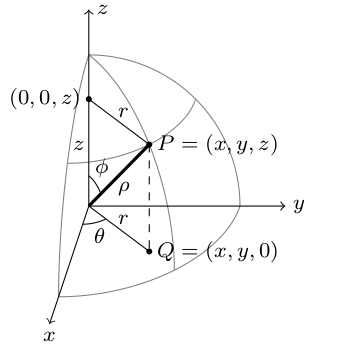
- Give the $(x,y,z)$ coordinates of the point in space whose spherical coordinates are $(\rho,\phi,\theta) = (3,\pi/2,\pi)$.
Solution
We're on a sphere of radius $rho =3$. The fact that $\phi=\pi/2$ means we've dropped 90 degrees from the positive $z$-axis, so we are in the $xy$-plane. With an angle of $\theta=\pi$, that puts us on the negative $x$-axis. The solution is $$(x,y,z)=(-3,0,0).$$
- Give $(\rho,\phi,\theta)$ coordinates for the Cartesian coordinates $(0,0,4)$, $(3,0,0)$, $(0,2,0)$, and $(0,0,-1)$.
Solution
A solution appears in the table below. When $\phi=0$ or $\phi=\pi$, the value of $\theta$ is arbitrary. You can of course add any multiple of $2\pi$ to any value of $\theta$ below, and still have a valid solution. $$\begin{array}{c|c} \text{Cartesian}&\text{Spherical}\\ (x,y,z)&(\rho,\phi,\theta)\\\hline (0,0,4)& (4,0,\text{any})\\ (3,0,0)& (3,\pi/2,0)\\ (0,2,0)& (2,\pi/2,\pi/2)\\ (0,0,-1)&(1,\pi,\text{any}) \end{array}$$
- Draw the region in space whose volume is computed from the triple integral $$\ds \int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{0}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$ Note that the Jacobian for spherical coordinates is $\rho^2\sin \phi$.
Solution
outerB = {theta, 0, Pi}
middleB = {phi, Pi/4, Pi/2}
innerB = {rho, 0, 3}
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, Evaluate[{outerB, middleB, innerB}]];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
- Consider the region $R$ satisfying $-1\leq x+y\leq 4$ and $0\leq 2x-y\leq 3$, the integral $\iint_RdA$, and the change-of-coordinates $u=x+y$ and $v=2x-y$.
- Draw the region $R$.
- Compute the Jacobians $\dfrac{\partial(u,v) }{\partial (x,y) }$ and $\dfrac{\partial(x,y) }{\partial (u,v) }$.
- Fill in the missing part of $\ds \iint_RdA = \int_{-1}^{4}\int_{0}^{3}?dvdu$. Then compute the integral.
- Try solving $\ds \iint_RxdA$, using the change-of-coordinates. What missing information will you need to find?
Solution
- The region is a parallelogram. Here are two ways to draw the region in Mathematica. The first skips entirely the change-of-coordinates, while the latter solves for $x$ and $y$ in terms of $u$ and $v$ first, and then uses the change of coordinates.
coordinates = {x, y} R = ParametricRegion[{coordinates, -1 <= x + y <= 4 && 0 <= 2 x - y <= 3}, {x, y}]; Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}] coordinates = {(u + v)/3, (2 u - v)/3} R = ParametricRegion[coordinates, {{u, -1, 4}, {v, 0, 3}}]; Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}] - The Jacobians are $\dfrac{\partial(u,v) }{\partial (x,y) } =\left|1(-1)-1(2)\right|= 3$ and $\dfrac{\partial(x,y) }{\partial (u,v) }=\frac{1}{3}$.
- The integral is $\ds \iint_RdA = \int_{-1}^{4}\int_{0}^{3}\dfrac{\partial(x,y) }{\partial (u,v) }dvdu = \int_{-1}^{4}\int_{0}^{3}\frac{1}{3}dvdu = \frac{1}{3}A = \frac{1}{3}(5\cdot 3) =5$.
- We need to solve for $x$ in terms of $u$ and $v$. For this particular problem, we can do that by simply adding the two equations $u=x+y$ and $v=2x-y$ together, which gives $u+v=3x$. Division by 3 yields $x = \frac{u+v}{3}$. We then have $$\ds \iint_RxdA = \int_{-1}^{4}\int_{0}^{3}\frac{u+v}{3}\frac{1}{3}dvdu.$$
We can do the solving with Mathematica.
Solve[{u == x+y, v== 2x-y}, {x,y}]
The Jacobians can be computed too, slightly modifying the code that worked for cylindrical and spherical. Notice that the code is the same
variables = {x,y}
coordinates = {x + y , 2 x-y}
jacobian = D[coordinates, {variables}] // Det // Abs // Simplify
variables = {u,v}
coordinates = {(u + v)/3, (2 u - v)/3}
jacobian = D[coordinates, {variables}] // Det // Abs // Simplify
This last option illustrates how you can incorporate the solving into the Jacobian process, and then compute the integral.
variables = {u, v};
uB = {u, -1, 4};
vB = {v, 0, 3};
coordinates = {x, y} /. (Solve[{u == x + y, v == 2 x - y}, {x, y}] // Flatten)
jacobian = D[coordinates, {variables}] // Det // Abs // Simplify
R = ParametricRegion[coordinates, Evaluate[{uB, vB}]];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]
area = Integrate[jacobian, uB, vB]
centroid = Integrate[coordinates*jacobian, uB, vB]/Integrate[jacobian, uB, vB]
Group Problems
- Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given, in cylindrical coordinates, by the iterated triple integral
$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$
Solution
You can use Mathematica to check your work.
coordinates = {r Cos[theta], r Sin[theta], z}
R = ParametricRegion[coordinates, {{r, 1, 3}, {theta, Pi/2, Pi}, {z, 0, 4}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
Here's the same thing, but with the bounds placed at the front of the code.
outerB = {r, 1, 3}
middleB = {theta, Pi/2, Pi}
innerB = {z, 0, 4}
coordinates = {r Cos[theta], r Sin[theta], z}
R = ParametricRegion[coordinates, Evaluate[{outerB, middleB, innerB}]];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
- Set up an integral formula to compute $\bar x$ for the solid above (use cylindrical coordinates).
Solution
No density is given, which means we interpret $\bar x$ as the $x$-coordinate of the centroid (so center of mass with $\delta=1$). This gives $$\bar x = \frac{\iiint_DxdV}{\iiint_DdV} = \frac{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}(r\cos\theta)rdz d\theta dr}{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr}.$$
We can compute all three coordinates of the centroid, with very little effort, using Mathematica.
ClearAll[r,theta,z](*useful if you defined r, theta, or z, somewhere previously.*)
outerB = {r, 1, 3};
middleB = {theta, Pi/2, Pi};
innerB = {z, 0, 4};
coordinates = {r Cos[theta], r Sin[theta], z};
jacobian = r;
Integrate[coordinates*jacobian, outerB, middleB, innerB]/
Integrate[jacobian, outerB, middleB, innerB]
% // N
- The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$.
- You can check your solution with Mathematica by updating the code below.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]} R = ParametricRegion[coordinates, {{rho, 0, 3}, {phi, Pi/4, Pi/2}, {theta, 0, Pi}}]; Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
- You can check your solution with Mathematica by updating the code below.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$. Check your work with Mathematica.
Some Solutions
Here is the region for part d.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
The corresponding integral is $$V=\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$
Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}]
Here is the region for part f.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
The corresponding integral is $$V=\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{8/ \cos\phi}\rho^2\sin\phi d\rho d\phi d\theta.$$
Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}]
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
