- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
Brain Gains (Rapid Recall, Jivin' Generation)

- Let $f(x,y) = x^2y^3$. Compute both $\frac{\partial f}{\partial x}$ and $\frac{df}{dx}$.
Solution
We have
- (assume $y$ is constant) $\frac{\partial f}{\partial x} = 2xy^3$ and
- (don't assume $y$ is constant) $\frac{df}{dx} = \frac{d}{dx}(x^2)y^3+x^2\frac{d}{dx}(y^3) = 2xy^3+3x^2y^2\frac{dy}{dx} = \frac{\partial f}{\partial x}\frac{dx}{dx} +\frac{\partial f}{\partial y}\frac{dy}{dx} $.
Note that if we were on a level curve of some function $f(x,y)$, then we would have $0 = \frac{\partial f}{\partial x}(1) +\frac{\partial f}{\partial y}\frac{dy}{dx}$, which means $\frac{dy}{dx} = -\frac{f_x}{f_y}$, a formula use in some disciplines to rapidly compute implicit derivatives. For example, to compute $\frac{dy}{dx}$ for the function $16 =x^2+3xy+y^2$, we have $f(x,y)=x^2+3xy+y^2$ and so $$\frac{dy}{dx} = -\frac{f_x}{f_y} = -\frac{2x+3y}{3x+2y}.$$ From first semester calculus, we would have started with $0=(2x)(1)+3x\frac{dy}{dx} +3y +(2y)\frac{dy}{dx}$, and then solved for $\frac{dy}{dx}$, obtaining the same solution.
- For the function $f(x,y)=x^3+3x^2+y^2+10y$, compute the second derivative.
Solution
Note $\frac{\partial}{\partial x} \vec\nabla f= (6x+6,0)$ and $\frac{\partial}{\partial y}\vec\nabla f = (0,2)$. Placing these vectors into the columns of a matrix gives us $$D^2f(x,y) = \begin{bmatrix}\begin{matrix}6x+6\\0\end{matrix}&\begin{matrix}0\\2\end{matrix}\end{bmatrix}.$$
- Find the critical points of the function $f(x,y)=x^3+3x^2+y^2+10y$.
Solution
There are two critical points, namely $(0,-5)$ and $(-2,-5)$. Note $\vec \nabla f(x,y) = (3x^2+6x,2y+10)$ is the zero matrix precisely when $x=0$ or $x=-2$, and $y=-5$.
- For the function $f(x,y)=x^3+3x^2+y^2+10y$, determine the location of any maxes, mins, or saddles, and classify each location appropriately using eigenvalues.
Solution
At each critical point, we need to (1) evaluate the second derivative, (2) compute the eigenvalues, and (3) classify the point using the eigenvalues.
- At the point $(0,-5)$, the second derivative is $D^2f(0,-5) = \begin{bmatrix}\begin{matrix}6\\0\end{matrix}&\begin{matrix}0\\2\end{matrix}\end{bmatrix}$. The eigenvalues are 6 and 2 (gradient point outwards from the point), which means at $(0,-5)$ we have a minimum.
- At the point $(-2,-5)$, the second derivative is $D^2f(-2,-5) = \begin{bmatrix}\begin{matrix}-6\\0\end{matrix}&\begin{matrix}0\\2\end{matrix}\end{bmatrix}$. The eigenvalues are -6 and 2 (gradient point outwards from the point in one direction, and inwards in another), which means at $(-2,-5)$ we have a saddle point.
- A rover travels along the curve $x^2+y=3$. The elevation near the rover is given by $z = 4 x - 2 y + 1395$. Locate the $(x,y)$ coordinates provided by Lagrange Multipliers.
Solution
We wish to optimize $f(x,y) = 4 x - 2 y + 1395$ subject to the constraint $g(x,y)=x^2+y=3$. We have $\vec\nabla f = (4,-2)$ and $\vec \nabla g = (2x,1)$. The system we must solve is $$4 = \lambda 2x, -2 = \lambda 1, x^2+y=3.$$ The second equation gives $\lambda = -2$. The first equation then provides $x=-1$. This means $y = 3-1 = 2$. The solution is $(x,y)=(-1,2)$.
- Imagine a rover follows a linear path through some terrain whose contour plot is given below.
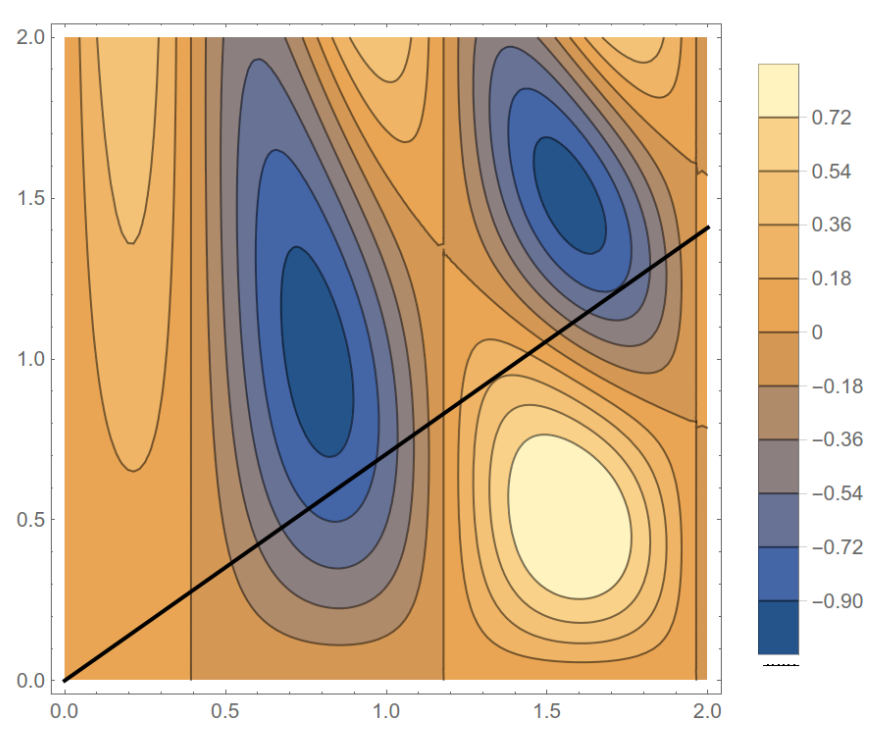
Identify the points that the Lagrange multipliers process will yield.
Solution
We'll discuss this in class. There are 4 points, namely the places where the path would meet a level curve tangentially. The one in the lower left corner is very subtle. Not all level curves are drawn, so we have to estimate some of these points.
Group Problems
- A rover travels along the curve $4x+y=3$. The elevation near the rover is given by $z=y-x^2$. Use Lagrange multipliers to locate the $(x,y)$ coordinates where the rover reaches maximum height. [Check: $(x,y)= (-2,11)$.]
- Suppose $h$ is a function of $p$ and $q$, where $p$ and $q$ are both functions of $x$, $y$, and $z$. Compute the partial derivatives of $h$ with respect to $x$, $y$, and $z$.
- For the function $f(x,y) = x^3+3xy+y^3$, the first and second derivatives are $$Df(x,y) = \begin{bmatrix}3x^2+3y&3x+3y^2\end{bmatrix}\quad\text{and}\quad D^2f(x,y) = \begin{bmatrix}\begin{matrix}6x\\3\end{matrix}&\begin{matrix}3\\6y\end{matrix}\end{bmatrix}. $$ A critical point of the function is $(x,y)=(-1,-1)$, which we can verify by computing $$Df(-1,-1) = \begin{bmatrix}3(-1)^2+3(-1)&3(-1)+3(-1)^2\end{bmatrix} = \begin{bmatrix}0&0\end{bmatrix}.$$ Does the function have a maximum or minimum at this critical point? Use the eigenvalues of $D^2f(-1,-1)$ to explain.
- Find the directional derivative of $f(x,y)=xy^2$ at $P=(4,-1)$ in the direction $(-3,4)$. [Check: $D_{(-3,4)}f(4,-1) = \vec\nabla f(4,-1)\cdot \frac{(-3,4)}{5}=(1,-8)\cdot \frac{(-3,4)}{5}=-35/5=-7$.]
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$. [Check: $(-2)(x-(-3))+(-3)(y-(-2))+2(1)(z-1)=0$. ]
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$. [Check: $z-4 = (-1)^2(x-4)+2(4)(-1)(y-(-1))$.]
- Consider the function $f(x,y,z) = 3xy+z^2$. We'll be analyzing the surface at the point $P=(1,-3,2)$.
- If $dx=0.1$, $dy=0.2$ and $dz=0.3$, then what is $df$ at $P$.
- Find the directional derivative of $f$ at $P$ in the direction $(1,-2,2)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $P$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- Consider the function $f(x,y)= 2x^2+3xy+4y^2-5x+2y$.
- Find all critical points of $f$. [Check: $(x,y) = (2,-1)$.]
- Determine the eigenvalues of the second derivative at each critical point. [Check: The eigenvalues are $\lambda = 6\pm\sqrt{13}$, so $\lambda \approx 9.6$ or $\lambda \approx 2.4$.]
- At each critical point, do we have a local max, local min, or saddle?
- A rover travels along the path $2x-4y=12$. The elevation is given by $z=x+y^2-3$. Use Lagrange multipliers to find the $(x,y)$ location of the lowest elevation reached by the rover along this path. [Check $ (4,-1) $.]
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
