• I-Learn, Class Pictures, Learning Targets, Text Book Practice
• Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus

We still have some tasks from Day 34 to finish discussing in class.

Day 34 - Prep

Task 34.1

It's time to focus on how area is changed when we perform a change-of-coordinates. We'll see that finding the area of a transformed parallelogram is the key.

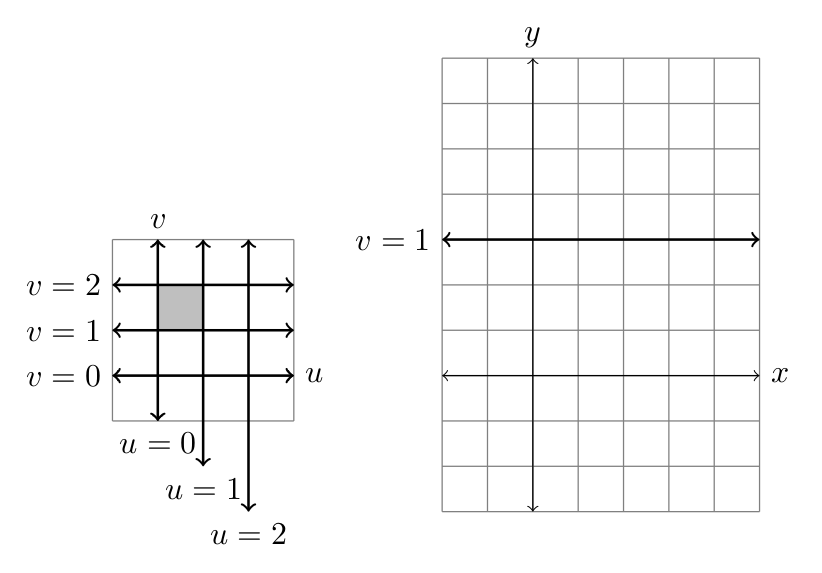
1. Consider the change-of-coordinates $x=2u$, $y=3v$.
   1. The lines $u=0,u=1,u=2$ and $v=0,v=1,v=2$ correspond to lines in the $xy$-plane. Draw these lines in the $xy$-plane (the line $v=1$ is done for you).
      • 
   2. The box in the $uv$-plane with $0\leq u\leq 1$ and $1\leq v\leq 2$ corresponds to a box in the $xy$-plane. Shade this box in the $xy$-plane and find its area.
   3. Compute the differentials $dx$ and $dy$. State them using the vector form (linear combination) $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix} ?\\ ?\end{pmatrix}du+\begin{pmatrix}?\\?\end{pmatrix}dv$$ What do the two vectors $(a,0)$ and $(0,b)$ have to do with your picture?
   4. Draw the box given by $-1\leq u\leq 1$ and $-1\leq v\leq 1$ in both the $uv$-plane and $xy$-plane. Then state the area $A_{uv}$ of this box in the $uv$-plane, and state the area $A_{xy}$ of the corresponding rectangle in the $xy$-plane.
   5. Consider the circle $u^2+v^2=1$, whose area inside is $A_{uv}=\pi$. Guess the area $A_{xy}$ inside the corresponding ellipse in the $xy$-plane. Explain.
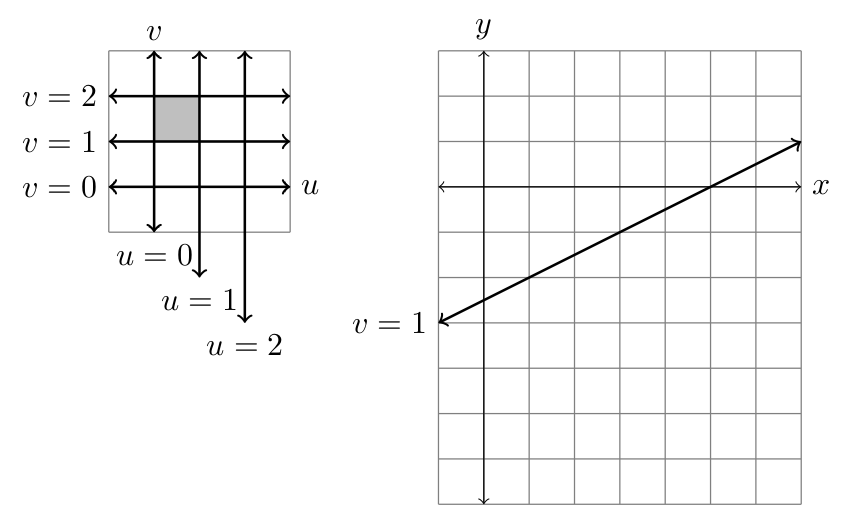
2. Consider now the change-of-coordinates $x=2u+v$, $y=u-2v$.
   1. The lines $u=0,u=1,u=2$ and $v=0,v=1,v=2$ correspond to lines in the $xy$ plane. Draw these lines in the $xy$-plane (the line $v=1$ is drawn for you). One option is to find the $xy$ coordinates of the $(u,v)$ points $(0,0)$, $(0,1)$, $(0,2)$, $(1,0)$, $(1,1)$, etc., and then just connect the dots to make a rotated grid.
      • 
   2. The box in the $uv$-plane with $0\leq u\leq 1$ and $1\leq v\leq 2$ should correspond to a parallelogram in the $xy$ plane. Shade this parallelogram in your picture above.
   3. Compute the differentials $dx$ and $dy$. State them using the vector form (linear combination) $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix} ?\\ ?\end{pmatrix}du+\begin{pmatrix}?\\?\end{pmatrix}dv.$$ What do the two vectors above have to do with your picture?
   4. Show that the area of the parallelogram formed using these two vectors is 5. How would you describe the change in area between the graph in the $uv$-plane, and the graph in the $xy$-plane?

The following code will help you check that your work on the second part is correct.

coordinates = {2 u + v, u - 2 v}
R = ParametricRegion[{coordinates, 0 <= u <= 1 && 1 <= v <= 2}, {u, v}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]
R = ParametricRegion[{coordinates, u == 0 || u == 1 || u == 2 || v == 0 || v == 1 || v == 2}, {{u, -1, 3}, {v, -1, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]

Task 34.2

Many vector fields are the derivative of a function. This function we call a potential for the vector field. Once we are comfortable finding potentials, we'll show that the work done by a vector field with a potential is the difference in the potential.

Potential of a Vector Field

A potential for the vector field $\vec F$ is a function $f$ whose gradient equals $\vec F$, so $\vec \nabla f=\vec F$.

Let's practice finding gradients and potentials. You're welcome to watch this YouTube Video before starting, or just jump in and give it a try.

1. Let $f(x,y) = x^2+3xy+2y^2$. Find $\vec \nabla f$. Then compute $D^2f(x,y)$ (you should get a square matrix). What are $f_{xy}$ and $f_{yx}$?
2. Consider the vector field $\vec F(x,y)=(2x+y,x+4y)$. Find the derivative of $\vec F(x,y)$ (it should be a square matrix). Then find a function $f(x,y)$ whose gradient is $\vec F$ (i.e. $Df=\vec F$). What are $f_{xy}$ and $f_{yx}$?
3. Consider the vector field $\vec F(x,y)=(2x+y,3x+4y)$. Find the derivative of $\vec F$. Why is there no function $f(x,y)$ so that $Df(x,y)=\vec F(x,y)$? [Hint: look at $f_{xy}$ and $f_{yx}$.]

Test for a Potential

Let $\vec F$ be a vector field that is everywhere continuously differentiable. Then $\vec F$ has a potential if and only if the derivative $D\vec F$ is a symmetric matrix. We say that a matrix is symmetric if interchanging the rows and columns results in the same matrix (so if you replace row 1 with column 1, and row 2 with column 2, etc., then you obtain the same matrix).

4. For each of the following vector fields, start by computing the derivative. Then find a potential, or explain why none exists.
   1. $\vec F(x,y)=(2x-y, 3x+2y)$
   2. $\vec F(x,y)=(2x+4y, 4x+3y)$
   3. $\vec F(x,y)=(2x+4xy, 2x^2+y)$
   4. $\vec F(x,y,z)=(x+2y+3z,2x+3y+4z,2x+3y+4z)$
   5. $\vec F(x,y,z)=(x+2y+3z,2x+3y+4z,3x+4y+5z)$
   6. $\vec F(x,y,z)=(x+yz,xz+z,xy+y)$

The Mathematica code below starts by computing the derivative $D\vec F$, then uses DSolve to find a potential, and finishes by computing the gradient of the potential to see if it is the original vector field (verify you have the correct solution). If a potential exists, then the last line should match the first. You'll need to add a third variable (,z) in appropriate spots to use this code for a 3D vector field.

ClearAll[F, f, x, y]
F = {2 x + y, x + 4 y}
D[F, {{x, y}}] // MatrixForm
potential = DSolve[D[f[x, y], {{x, y}}] == F, f[x, y], {x, y}]
D[f[x, y] /. potential, {{x, y}}] // Flatten

Task 34.3

We already found the area of parallelogram in the $xy$-plane. To use new coordinate systems in 3D, we'll need to volume of a parallelepiped formed by the three vectors $\vec u$, $\vec v$, and $\vec w$, shown in the image below.

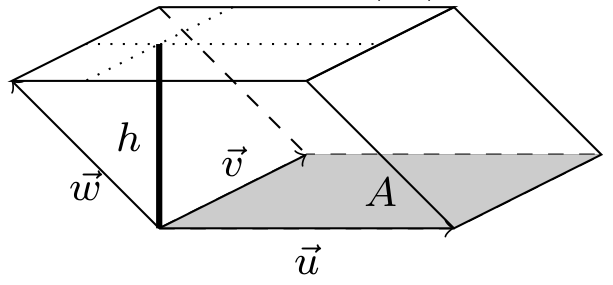
We get the volume by obtaining the area $A$ of one face, multiplied by the distance $h$ between the base and the plane containing the opposing face. This means we need to (1) compute the area of a parallelogram in 3D, and then (2) obtain a formula for the distance between the opposing faces. In this task, we'll see that the cross product and dot product provide us with precisely the tools we need to do both tasks.

1. Let $\vec u = (a,b,c)$ and $\vec v = (d,e,f)$. Our goal is to find the area of a parallelogram whose edges are formed from these two vectors.
   1. Draw a picture that contains 2 vectors labeled $\vec u$ and $\vec v$. In that picture, include $\vec u_{\parallel \vec v}$ and $\vec u_{\perp\vec v}$. Explain why the area we seek is $A = |\vec u_{\perp\vec v}||\vec v|$. Then use the following Mathematica code to compute the area. The Assumptions command below is needed to help Mathematica do some simplifications .

      $Assumptions = a \[Element] Reals && b \[Element] Reals && c \[Element] Reals && d \[Element] Reals && e \[Element] Reals && f \[Element] Reals;
      u = {a, b, c};
      v = {d, e, f};
      uPerpv = u - Projection[u, v];
      Norm[uPerpv]*Norm[v] // Simplify
      

   2. The magnitude of the cross product is $$|\vec u\times \vec v|= |(bf-ce, cd-af, ae-bd)| = \sqrt{(bf-ce)^2+ (cd-af)^2+ (ae-bd)^2}.$$ Show that the magnitude of the cross product and the area of the parallelogram (the value you obtained above) are the same. You can do this by hand, or with Mathematica. If you choose to use Mathematica, here is code for getting the magnitude of the cross product.

      Norm[Cross[u, v]] // Simplify
      

   3. Use what you just learned to find the area of the parallelogram formed by the two vectors $(1,2,3)$ and $(-3,1,4)$.

Properties of the Cross Product

The cross product $\vec u\times\vec v$ of $\vec u$ and $\vec v$ is orthogonal to both $\vec u$ and $\vec v$. The magnitude of the cross product, so $|\vec u\times \vec v|$, is the area of the parallelogram formed by $\vec u$ and $\vec v$.

Now that we have a formula for the area of one face of a parallelepiped, we only need to find the distance between opposing faces to obtain the volume.

2. Consider three vectors $\vec u$, $\vec v$, and $\vec w$ in $\mathbb{R}^3$. We will find the volume of the parallelepiped formed by these three vectors. Let the base of the parallelogram be the face formed by $\vec u$ and $\vec v$. The height $h$ is the distance between the plane that contains the base and the plane that contain the opposing side of the parallelepiped.
   1. Give a formula to compute the area of the base of the parallelogram. (What did the first part of this tasks help us learn)
   2. Give a vector $\vec n$ that is normal to the base.
   3. Use the projection formula, with the vectors $\vec w$ and $\vec n$ in an appropriate manner, to state the height $h$ of the parallelogram in terms of dot products.
   4. Use your work above to explain why the parallelepiped's volume is $$V=|(\vec u\times \vec v)\cdot \vec w|.$$

Triple Product

We call $(\vec u\times \vec v)\cdot \vec w$ the triple product of $\vec u$, $\vec v$, and $\vec w$. The volume of a parallelepiped formed by the three vectors is $V=|(\vec u\times \vec v)\cdot \vec w|.$

Task 34.4

Pick some problems related to the topics we are discussing from the Text Book Practice page.

Day 35 - Prep

Task 35.1

1. Use the area of a parallelogram formula we developed to explain why the Jacobian can be computed using the formula $$\frac{\partial (x,y)}{\partial (u,v)} = \left|\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\right|.$$
2. For the polar coordinate transformation given by the change-of-coordinates $x=r\cos\theta$ and $y=r\sin\theta$, compute the differential $(dx,dy)$, and then show that the Jacobian is $\ds\frac{\partial (x,y)}{\partial (r,\theta)} = |r|$. This is precisely the reason we use the notation $dA = |r|drd\theta$ when setting up double integrals using polar coordinates.
3. For the change-of-coordinates $x=2u-v$ and $y=u+2v$, compute the differential $(dx,dy)$, and then obtain the Jacobian $\ds \frac{\partial (x,y)}{\partial (u,v)}$.
4. For the change-of-coordinates $x=au$ and $y=bv$, show that the Jacobian is $\ds \frac{\partial (x,y)}{\partial (u,v)}=|ab|$.
5. For the change-of-coordinates $u=x+y$ and $v=x-y$, show that $\ds \frac{\partial (u,v)}{\partial (x,y)} = 2$.
6. For the change-of-coordinates $u=x+y$ and $v=x-y$, first solve for $x$ and $y$ in terms of $u$ and $v$ (so obtain $x = ....$ and $y= ...$). Then show that $\ds \frac{\partial (x,y)}{\partial (u,v)} = \frac{1}{2}$.

Did you notice that $\ds \frac{\partial (u,v)}{\partial (x,y)} = \left(\ds \frac{\partial (x,y)}{\partial (u,v)}\right)^{-1}$?

Task 35.2

In three dimensions, some common coordinate systems are cylindrical and spherical coordinates. In this task, for each of these coordinates systems, we'll (1) develop the change-of-coordinates formula, (2) compute the Jacobian using the triple product, and then (3) use the Jacobian to compute the volume of an object in this coordinate system.

Let's first tackle cylindrical coordinates. Let $P=(x,y,z)$ be a point in space. This point lies on a cylinder of radius $r$, where the cylinder has the $z$ axis as its axis of symmetry. The height of the point is $z$ units up from the $xy$ plane. The point casts a shadow in the $xy$ plane at $Q=(x,y,0)$. The angle between the ray $\vec{Q}$ and the $x$-axis is $\theta$. See the image below.

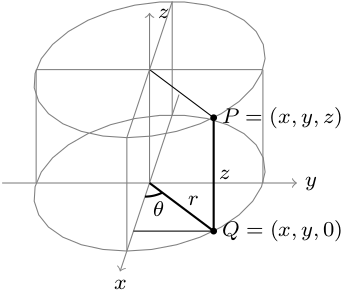
1. Explain why the equations for cylindrical coordinates are $$x=r\cos\theta, \quad y=r\sin\theta,\quad z=z.$$ [Hint: Compute the sine and cosine of $\theta$ in terms of $x$, $y$, and $r$, and then solve for $x$ and $y$.]
2. Compute the Jacobian $\dfrac{\partial(x,y,z)}{\partial(r,\theta,z)}$ for cylindrical coordinates. The steps below are a guide, if needed.
   • For cylindrical coordinates we have $x=r\cos\theta$, $y=r\sin\theta$, and $z=z$. Write the differential $d(x,y,z)$ as the linear combination of partial derivatives $$\begin{pmatrix}dx\\dy\\dz\end{pmatrix} = \begin{pmatrix}\cos\theta\\\sin\theta\\0\end{pmatrix}dr+\begin{pmatrix}?\\?\\?\end{pmatrix}d\theta+\begin{pmatrix}?\\?\\?\end{pmatrix}dz.$$
   • Compute the volume of the parallelepiped formed by the three vectors (partial derivatives) above, using the triple product. Software can make quick work of this. Simplify your result to show that $\dfrac{\partial(x,y,z)}{\partial(r,\theta,z)} = |r|$.
3. Consider the solid domain $D$ in space that lies inside the right circular cylinder $x^2+y^2=a^2$ (or $r=a$) for $0\leq z\leq h$. Start by drawing the domain $D$. The volume in cylindrical coordinates is given by the iterated integral $$V = \iiint_D dV = \ds\int_{0}^{2\pi}\int_{0}^{a}\int_{0}^{h}rdzdrd\theta.$$ Compute this integral to obtain a familiar formula $V = \pi a^2 h$.

Now let's tackle spherical coordinates. Let $P=(x,y,z)$ be a point in space. This point lies on a sphere of radius $\rho$ ("rho"), where the sphere's center is at the origin $O=(0,0,0)$. The point casts a shadow in the $xy$ plane at $Q=(x,y,0)$. The angle between the ray $\vec{Q}$ and the $x$-axis is $\theta$, which some call the azimuth angle. The angle between the ray $\vec{P}$ and the $z$-axis is $\phi$ ("phi"), which some call the inclination angle, polar angle, or zenith angle. See the image below.

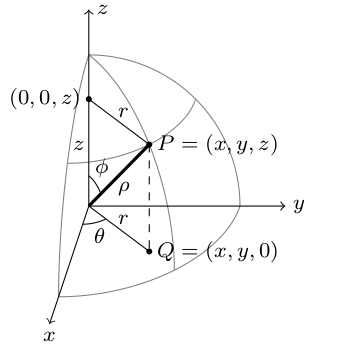
4. Explain why the equations for spherical coordinates are $$x=\rho\sin\phi\cos\theta,\quad y=\rho\sin\phi\sin\theta,\quad z=\rho\cos\phi.$$ [Hint: Compute the sine and cosine of $\phi$ in terms of $\rho$, $r$, and $z$, and then solve for $r$ and $z$. Substitution into $x=r\cos\theta$ and $y=r\sin \theta$ will get the rest.]
5. Compute the Jacobian $\dfrac{\partial(x,y,z)}{\partial(\rho,\phi,\theta)}$ for spherical coordinates. The steps below are a guide, if needed.
   • For spherical coordinates we have $$x=\rho\sin\phi\cos\theta,\quad y=\rho\sin\phi\sin\theta,\quad z=\rho\cos\phi.$$ Write $d(x,y,z)$ as a linear combination of partial derivatives, so $$\begin{pmatrix}dx\\dy\\dz\end{pmatrix} = \begin{pmatrix}\sin\phi\cos\theta\\\sin\phi\sin\theta\\\cos\phi\end{pmatrix}d\rho+\begin{pmatrix}?\\?\\?\end{pmatrix}d\phi+\begin{pmatrix}?\\?\\?\end{pmatrix}d\theta.$$
   • Compute the volume of the parallelepiped formed by the three vectors (partial derivatives) above. Software can make quick work of this. You can do it all by hand, but you'll have to use a Pythagorean identity several times to complete the simplification. Simplify your result to show that $\frac{\partial(x,y,z)}{\partial(\rho,\phi,\theta)} = |\rho^2\sin\phi|$.
6. Consider the solid domain $D$ in space that lies inside the sphere $x^2+y^2+z^2=a^2$ (or $\rho=a$). Start by drawing the domain $D$. The volume in spherical coordinates is given by the iterated integral $$V = \iiint_D dV = \ds\int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{a}\rho^2\sin\phi d\rho d\phi d\theta.$$ Compute this integral to obtain a familiar formula $V = \frac{4}{3}\pi a^3$.

Task 35.3

For a differentiable function $f(x)$, the second part of the fundamental theorem of calculus states that $\ds\int_a^b \frac{df}{dx} dx =f(b)-f(a)$. To find the total change in a function $f$ (so $f(b)-f(a)$), we just sum the little changes $\int_C df = \int_C \frac{df}{dx}dx$. We'll use this fact to greatly simplify work computations for vector fields that have a potential.

Let $\vec F$ be a vector field with $f$ being a potential for $\vec F$, meaning $\vec F = \vec \nabla f$. Let $\vec r(t)$ for $a\leq t\leq b$ be a differentiable parametrization of a curve $C$. Let $A = \vec r(a)$ and $B= \vec r (b)$ be the end points of the curve. The composite function $g(t) = f(\vec r(t)) = (f\circ \vec r)(t)$ gives the potential at points along the curve. In particular $f(A)$ and $f(B)$ give the potential at the end points of the curve. The difference in potential is $f(B)-f(A)$.

1. Pause. Reread the above. Do you understand what each of $\vec F$, $f$, $\vec r$, $a$, $b$, $A$, $B$, and $g$ represent? If not, what parts do you have questions about? Then continue reading.

From the chain rule, the composite function $g(t) = f(\vec r(t)) = (f\circ \vec r)(t)$ has the derivative $\frac{dg}{dt}=\vec \nabla f(\vec r(t))\cdot\frac{d\vec r}{dt}$. We now compute $$\begin{align*} f(B)-f(A) &= f(\vec r(b))-f(\vec r(a))&\text{($A$ and $B$ are the end points of the curve)}\\ &= g(b)-g(a)&\text{(recall $g(t) = f(\vec r(t))$}\\ &= \int_a^b \frac{dg}{dt}dt&\text{(the fundamental theorem of calculus)}\\ &= \int_a^b \vec \nabla f(\vec r(t))\cdot \frac{d\vec r}{dt} dt&\text{(using the chain rule to compute $\frac{dg}{dt}$)}\\ &= \int_C \vec F\cdot d\vec r&\text{(recall that $\vec \nabla f=\vec F$)}. \end{align*}$$ This shows that the work done by $\vec F$ along $C$ is the difference in the potential $f$.

Let's try using this theorem in a few situations.

2. Let $\vec F(x,y) = (2x+y,x+4y)$ and $C$ be the parabolic path $\vec r(t) = (t,9-t^2)$ for $-3\leq t\leq 2$.
   1. Use the work formula we developed earlier in the semester, so $\int_C Mdx+Ndy$ or $\int_C \vec F\cdot d\vec r$, to set up and compute the work done by $\vec F$ along $\vec r$. This is a review of a previous learning target. Feel free to use software to complete the integral.
   2. Find a potential $f$ for $\vec F$, state $A$ and $B$, and then compute $f(B)-f(A)$.
   3. Identify the function $g(t) = f(\vec r(t))$, compute $\frac{dg}{dt}$, state $\vec F(\vec r(t))$ and $\frac{d\vec r}{dt}$, and then verify that $\frac{dg}{dt} = \vec F(\vec r(t))\cdot \frac{d\vec r}{dt}$ (these were the terms that appeared in the proof of the fundamental theorem of line integrals).
3. Let $\vec F(x,y,z) = (2x+yz,2z+xz,2y+xy)$ and $C$ be the straight segment from $(2,-5,0)$ to $(1,2,3)$. Compute the work done by $\vec F$ along $C$ by first finding a potential for $\vec F$.
4. Let $\vec F = (x,2yz,y^2)$. Let $C$ be the curve which starts at $(1,0,0)$ and follows a helical path $(\cos t, \sin t, t)$ to $(1,0,2\pi)$ and then follows a straight line path to $(2,4,3)$. Find the work done by $\vec F$ to get from $(1,0,0)$ to $(2,4,3)$ along this path.
5. Suppose a vector field $\vec F$ has a potential. Compute $\int_C \vec F\cdot d\vec r$ where $C$ is the path parametrized by $\vec r(t) = (3\cos t, 3\sin t)$ for $0\leq t\leq 2\pi$.

Task 35.4

Pick some problems related to the topics we are discussing from the Text Book Practice page.

Day 35 - In class

Brain Gains (Rapid Recall, Jivin' Generation)

• Consider the vector field $\vec F(x,y,z) = (2x+3z, 4y,3x-3z^2)$ and the helical curve $C$ parametrized by $\vec r(t) = (t, \cos (\pi t), \sin(\pi t))$ for $0\leq t\leq 2$.
  • Find a potential for $\vec F$.
  • Find work done by $\vec F$ to move an object along $C$.

ClearAll[F, f, r, potential]
F[x_, y_, z_] := {2 x + 3 z, 4 y, 3 x - 3 z^2}
sol = DSolve[D[f[x, y, z], {{x, y, z}}] == F[x, y, z], f, {x, y, z}] //Flatten
potential = f /. sol;

(*Manually type in the end points*)
potential[2, 1, 0] - potential[0, 1, 0]

(*Use function notation to evaluate the potential at the end points.*)
r[t_] := {t, Cos[Pi t], Sin[Pi t]}
potential @@ r@2 - potential @@ r@0 

(*The apply function (@@) is required for function composition when the output is a vector.*)
(*Here we compute work using the formula from earlier in the semester*)
Integrate[Dot[Apply[F, r[t]], D[r[t], t]], {t, 0, 2}] 
Integrate[Dot[F @@ r@t, r'@t], {t, 0, 2}]

• Consider the integral $\iint_RdA$, the region satisfying $-1\leq x+y\leq 4$ and $0\leq 2x-y\leq 3$, and the change-of-coordinates $u=x+y$ and $v=2x-y$.
  • Draw the region $R$.
  • Compute the Jacobians $\dfrac{\partial(u,v) }{\partial (x,y) }$ and $\dfrac{\partial(x,y) }{\partial (u,v) }$.
  • Fill in the missing part of $\ds \iint_RdA = \int_{-1}^{4}\int_{0}^{3}?dvdu$, and then evaluate the integral.
  • Try solving $\ds \iint_RxdA$, using the change-of-coordinates. What missing information will you need to find?

coordinates = {x, y}
R = ParametricRegion[{coordinates, -1 <= x + y <= 4 && 0 <= 2 x - y <= 3}, {x, y}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]

coordinates = {(u + v)/3, (2 u - v)/3}
R = ParametricRegion[coordinates, {{u, -1, 4}, {v, 0, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]

• Give the $(x,y,z)$ coordinates of the point in space whose spherical coordinates are $(\rho,\phi,\theta) = (3,\pi/2,\pi)$.

• Give $(\rho,\phi,\theta)$ coordinates for the Cartesian coordinates $(0,0,4)$, $(3,0,0)$, $(0,2,0)$, and $(0,0,-1)$.

• Draw the region in space whose volume is computed from the triple integral $$\ds \int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{0}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$

coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{rho, 0, 3}, {phi, Pi/4, Pi/2}, {theta, 0, Pi}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]

Group Problems

1. Compute the work done by the vector field $\vec F = (4x+2xy,x^2+2y)$ along the curve $C$ parametrized by $\vec r(t) = (3t-1,-5t+2)$ for $0\leq t\leq 1$. [Hint: First find a potential.]

2. Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given, in cylindrical coordinates, by the iterated triple integral

$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$

coordinates = {r Cos[theta], r Sin[theta], z}
R = ParametricRegion[coordinates, {{r, 1, 3}, {theta, Pi/2, Pi}, {z, 0, 4}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]

3. Set up an integral formula to compute $\bar x$ for the solid above (use cylindrical coordinates).

4. Give cylindrical equations for both the the sphere $x^2+y^2+z^2=9$ and paraboloid $z=9-x^2-y^2$.

5. The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
   1. Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
   2. Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
   3. Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
   4. Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$.
      • You can check your solution with Mathematica by updating the code below.

        coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
        R = ParametricRegion[coordinates, {{rho, 0, 3}, {phi, Pi/4, Pi/2}, {theta, 0, Pi}}];
        Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
        

   5. Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
   6. Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$. Check your work with Mathematica.

coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]

Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}]

coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]

Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}]

Day 36 - Prep

Task 36.1

This task has you practice using spherical and cylindrical coordinates. Mathematica's ParametricRegion[] command allows us to plot a region, using any coordinate system, which is extremely useful for visualizing regions defined by bounds of an integral. As an example, the code below visualizes the region whose volume is given by the cylindrical coordinate iterated triple integral $$\int_{1}^{3}\int_{\pi/2}^{2\pi}\int_{0}^{r}rdz d\theta dr,$$ and then computes the triple integral.

coordinates = {r Cos[theta], r Sin[theta], z}
R = ParametricRegion[coordinates, {{r, 1, 3}, {theta, Pi/2, 2 Pi}, {z, 0, r}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
Integrate[r, {r, 1, 3}, {theta, Pi/2, 2 Pi}, {z, 0, r}]

To compute integrals in spherical coordinates, we just update the change-of-coordinates and bounds. Here's code to plot the region whose volume is given by the spherical coordinate iterated triple integral $$\ds \int_{0}^{\pi}\int_{\pi/6}^{\pi/3}\int_{1}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$

coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, Pi/2}, {phi, Pi/6, Pi/3}, {rho, 1, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
Integrate[rho^2 Sin[phi], {theta, 0, Pi/2}, {phi, Pi/6, Pi/3}, {rho, 1, 3}]

1. Consider the solid domain $D$ in space which is above the cone $z=\sqrt{x^2+y^2}$ and below the paraboloid $z=6-x^2-y^2$.
   1. Sketch the region by hand.
   2. Explain why an equation of the cone in cylindrical coordinates is $z=r$. Then obtain an equation of the paraboloid in cylindrical coordinates.
   3. Use cylindrical coordinates to set up an iterated triple integral that would give the volume of the region. You'll need to find where the surfaces intersect, as their intersection will help you determine the appropriate bounds. Use the ParametricRegion[] command to verify that the bounds you gave do indeed produce the correct region.
   4. By symmetry, it should be clear that for the centroid of this region, we have $\bar x = \bar y = 0$. Set up a formula involving iterated triple integrals that would give $\bar z$ for this solid, and then use software to compute $\bar z$.
2. Consider the solid domain $D$ in space that lies below the cone $z=\sqrt{x^2+y^2}$, above the $xy$-plane, and inside the sphere $x^2+y^2+z^2=25$.
   1. Provide a sketch of the domain $D$.
   2. Explain why an equation of the cone in spherical coordinates is $\phi = \pi/4$. Then given an equation of the sphere in spherical coordinates.
   3. Set up an integral in spherical coordinates that gives the volume of $D$. Use the ParametricRegion[] command to verify that the bounds you gave do indeed produce the correct region.
   4. Set up an integral in spherical coordinates that would give the $z$-coordinate of the centroid of $D$.

Task 36.2

Two important vector fields show up over and over again when studying gravity and electrostatics. In this task we will develop a common formula for these fields, show that these fields have a potential, and then practice using the fundamental theorem of line integrals to perform work computations, using the potential.

1. We need a formula for a vector field where at each point in space, the vector points towards the origin with a magnitude that proportional to 1 over the square of the distance to the origin. To obtain this field, complete the following steps.
   1. Let $P=(x,y,z)$ be a point in space. At the point $P$, let $\vec F_1(x,y,z)$ be the vector which points from $P$ to the origin. Give a formula for $\vec F_1(x,y,z)$.
   2. Give an equation of the vector field where at each point $P$ in space, the vector $\vec F_2(P)$ is a unit vector that points towards the origin.
   3. Give an equation of the vector field where at each point $P$ in space, the vector $\vec F_3(P)$ is a vector of length 7 that points towards the origin.
   4. Give an equation of the vector field where at each point $P$ in space, the vector $\vec F(P)$ points towards the origin, and has a magnitude equal to $G/d^2$ where $d = \sqrt{x^2+y^2+z^2}$ is the distance to the origin, and $G$ is a constant.
2. The gravitational vector field is directly related to the radial field $\ds\vec F(x,y,z) = \frac{\left(-x,-y,-z\right)}{(x^2+y^2+z^2)^{3/2}}$.
   1. We say that a vector field is conservative when the work done by the field is independent of the path traveled. Show that this vector field is conservative, by finding a potential for $\vec F$.
   2. Compute the work done by $\vec F$ to move an object from $(1,2,-2)$ to $(0,-3,4)$ along ANY path that avoids the origin.

Task 36.3

We need to gain some familiarity with the notation related to gradients, divergence, and curl. As you work on the tasks below, you are welcome to use subscript notation (such as $f_x$ and $M_y$) to simplify writing.

1. Suppose $f(x,y,z)$ is twice continuously differentiable.
   1. Compute the curl of the gradient of $f$, so compute $\vec \nabla \times \vec \nabla f$. Simplify the result as much as possible.
   2. If a vector field $\vec F = (M,N,P)$ has a potential, then what is the curl of $\vec F$?
2. Suppose $\vec F(x,y,z) = (M,N,P)$ is a vector field and $f(x,y,z)$ is a function, both of which are twice continuously differentiable.
   1. Compute the divergence of the curl of $\vec F$, so compute $\vec \nabla \cdot \left(\vec \nabla \times \vec F\right)$, and simplify the result as much as possible.
   2. Compute the divergence of the gradient of $f$, so compute $\vec \nabla \cdot \vec \nabla f$, and simplify the result as much as possible.

Task 36.4

Pick some problems related to the topics we are discussing from the Text Book Practice page.

Today

• Sep24, Oct, Nov, Dec