- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
We still have some tasks from Day 25 to finish discussing in class.
Day 25 - Prep
We are beginning a new unit on integration.
Task 25.1
We need to become adept at describing regions in the plane, using inequalities. For this first task, we'll start with inequalities and from them shade a region in the plane.
- Shade the region in the $xy$-plane that satisfies the inequalities $-1\leq x\leq 1$ and $1-x\leq y\leq 4-x^2$.
- Shade the region in the $xy$-plane that satisfies the inequalities $-3\leq y\leq 0$ and $0\leq x\leq \sqrt{9-y^2}$.
- Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $0\leq \theta\leq \pi$ and $1\leq r\leq 3$.
- Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $-\frac{\pi}{6}\leq \theta \leq \frac{\pi}{6}$ and $0\leq r\leq 4\cos 3\theta$.
- Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $0\leq \theta\leq \frac{3\pi}{2}$ and $1\leq r\leq 3+2\cos\theta$.
We can also describe solid regions in space, using 3 sets of inequalities.
- Draw the region in space that satisfies the inequalities $0\leq x\leq 3$, $-1\leq y\leq 1$, and $0\leq z\leq 1-y^2$.
- Draw the region in space that satisfies the inequalities $-1\leq x\leq 1$, $0\leq y\leq 1-x^2$, and $0\leq z\leq 1-y$.
We will soon see that the area of the first region is given by the iterated double integral $\ds\int_{x=-1}^{x=1}\left(\int_{y=1-x}^{y=4-x^2}dy\right) dx$, written more compactly as $\ds\int_{-1}^{1}\int_{1-x}^{4-x^2}dy dx.$ The area of the second region is given by $\ds\int_{-3}^{0}\int_{0}^{\sqrt{9-y^2}}dx dy.$
The polar regions have areas given by the iterated double integrals $\ds\int_{0}^{\pi}\int_{1}^{3}rdr d\theta$, $\ds\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\int_{0}^{4\cos 3\theta}rdr d\theta$, and $\ds\int_{0}^{\frac{3\pi}{2}}\int_{1}^{3+2\cos\theta}rdr d\theta$.
The regions in space have a volume given by the iterated triple integrals $\ds\int_{0}^{3}\int_{-1}^{1}\int_{0}^{1-y^2}dz dy dx$ and $\ds\int_{-1}^{1}\int_{0}^{1-x^2}\int_{0}^{1-y}dz dy dx$.
Task 25.2
One way to compute the area of a region $R$ is overlay the region with a rectangular grid, where $dx$ and $dy$ are the distances between the vertical and horizontal lines of the grid. To find the area of the region, we first determine which of the rectangles contains a portion of the region $R$, and then add up the areas of of all such rectangles. This will overestimate the area, but we can then use limits to shrink both $dx$ and $dy$ to zero to obtain the area.
Consider the polar curve $r=1+\cos\theta$. We will use the approach described above to estimate the area of region $R$ that is inside this polar curve. We'll assume that all distances are given in meters. The bounds for each graph below are $-1\leq x\leq 2$ and $-2\leq y\leq 2$.
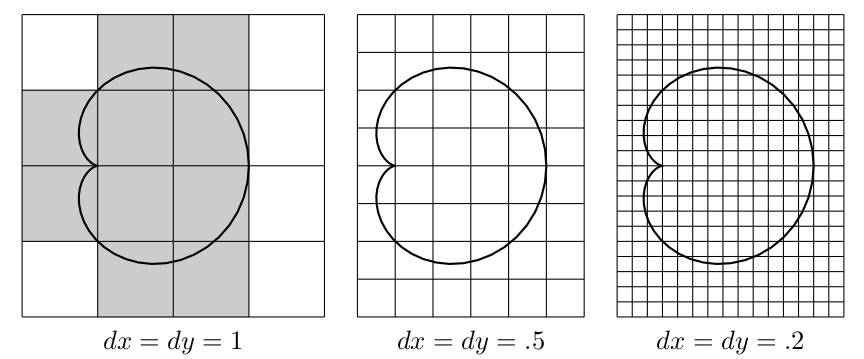
- For the first picture above, there are 10 rectangles (shaded) that contain a portion of the region $R$. Each of these rectangles has area $dA=dxdy=(1)(1) = 1 $, which means an overestimate for the area of $R$ is $A\approx 10 \, dA = 10(1)=10$. Describe a way to use these same rectangles to get an underestimate for the area of $R$.
- Now use the middle picture above (where $dx=dy=.5$) to shade and then count the number of rectangles that contain a portion of $R$. What is the area $dA$ of each little rectangle. Finish by giving an estimate for $A$.
- Now use the last picture with $dx=dy=.2$ to estimate the area of $R$.
- How can we obtain the exact value for the area of $R$?
- The questions above help focus on finding area, because each rectangle was given the same importance in the overall sum. Suppose instead that an object is made in the shape of the cardioid, but the portion that lies above the $x$-axis has a density of 2 kg/m^2, while the portion below has a density of 3 kg/m^2. How would you modify your work above to give an estimate for the mass (in kg)?
Task 25.3
In this task, we'll focus on the integrals $\int_C dx$ and $\int_C dy$, and from them develop a way to compute area using iterated (repeated) integrals.
- Consider the portion of the ellipse parametrized by $\vec r(t) = (3\cos t, 4\sin t)$ for $0\leq t\leq \pi/2$. Notice that parametrization starts at $(3,0)$ and ends at $(0,4)$. The integral $\int_C dx$ literally says ``Sum up little changes in $x$.'' Adding up little changes in $x$ gives the total change in $x$.
- Differentials gives us $dx = -3\sin t dt$. Compute $\ds\int_C dx=\int_{t=0}^{t=\pi/2}dx = \ds\int_{t=0}^{t=\pi/2}-3\sin t dt$ and verify that it gives the total change in $x$ from $t=0$ to $t=\pi/2$.
- Guess the value of $\ds\int_{t=0}^{t=\pi/2}dy$ (the integral adds up what?), and then check your solution.
- Consider the region $R$ between the functions $y=x^2$ and $y=-x$ for $0\leq x\leq 3$. Our goal is to explain why the iterated integral $\ds\int_{x=0}^{x=3}\left(\int_{y=-x}^{y=x^2} dy \right)dx$ gives the area of the region $R$.
- Draw both functions and shade the region $R$.
- Compute the integral $\ds\int_{y=-x}^{y=x^2}dy$ for arbitrary $x$. This integral comutes, for a given value of $x$, the total change in $y$ (so a height).
- Recall that $dx$ is a small width. When we multiply the previous integral by this width $dx$, we will obtain the area of a small rectangular region whose height is given by $\ds\int_{y=-x}^{y=x^2}dy$ and width is given by $dx$. Pick a value $x$ between 0 and 3, and then construct a picture that illustrates this rectangular region whose area is given by $dA=\ds\left(\int_{y=-x}^{y=x^2} dy \right)dx$.
- Explain why $\ds\int_{x=0}^{x=3}\left(\int_{y=-x}^{y=x^2} dy \right)dx$ gives the area of the region $R$.
- Consider the double integral $$\int_{y=-1}^{y=2}\left(\int_{x=y^2}^{x=y+2}dx\right)dy.$$
- The bounds in the integral above describe a region in $xy$ plane where $-1\leq y\leq 2$ and $y^2\leq x\leq y+2$. Sketch this region.
- Consider the inner integral $\int_{x=y^2}^{x=y+2}dx$. This integral adds up changes in $x$, so gives a total change in $x$ (hence a width). Add to your sketch several line segments whose widths are given by this integral.
- When we multiply a width $\int_{x=y^2}^{x=y+2}dx$ by a small height $dy$, we get a little bit of area $dA$. Pick a value $y$ between $-1$ and $2$, and then at that height draw a small rectangle whose area is given by $dA = \left(\int_{x=y^2}^{x=y+2}dx\right) dy$.
- Adding up little bits of area gives total area, so the double integral $$\int_{y=-1}^{y=2}\left(\int_{x=y^2}^{x=y+2}dx\right)dy$$ gives an area. Compute the integral.
Task 25.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
Day 26 - Prep
Task 26.1
In this task we'll be focusing on locating the average, mean, center, etc., of something.
- Suppose a class takes a test and there are three scores of 70, five scores of 85, one score of 90, and two scores of 95. We will calculate the average class score, $\bar s$, four different ways to emphasize four ways of thinking about the averages. We are emphasizing the pattern of the calculations in this problem, rather than the final answer, so it is important to write out each calculation completely, without doing any simplifying, before calculating the number $\bar s$.
- Compute the average by adding 11 numbers together and dividing by the number of scores ($\bar s=\frac{\sum \text{values}}{\text{number of values}}$). Write down the whole computation before doing any arithmetic.
- Compute the numerator of the fraction in the previous part by multiplying each score by how many times it occurs, rather than adding it in the sum that many times ($\bar s=\frac{\sum (\text{value}\cdot\text{weight})}{\sum \text{weight}}$). Again, write down the calculation for $\bar s$ before doing any arithmetic.
- Compute $\bar s$ by splitting up the fraction in the previous part into the sum of four numbers ($\bar s=\sum (\text{value}\cdot\text{(\% of stuff)})$). This is called a weighted average because we are multiplying each score value by a weight.
- Another way of thinking about the average $\bar s$ is that $\bar s$ is the number so that if all 11 scores were the same value $\bar s$, you'd have the same sum of scores ($\text{ (number of values) }\bar s = \sum \text{values}$ or $(\sum \text{weight})\bar s = \sum (\text{value}\cdot\text{weight})$). Write this way of thinking about these computations by taking the formulas for $\bar s$ in the first two parts and multiplying both sides by the denominator.
We now generalize the above ways of thinking about averages from a discrete situation to a continuous situation. We did this in first-semester calculus when we computed the average value of $f$ using integrals.
- Suppose the price of a stock is \$10 for two days. Then the price of the stock jumps to \$20 for three days. Our goal is to determine the average price of the stock over the total 5 day period.
- Why is the average stock price not \$15? Use any of the methods from the previous problem to show that the average price is $\bar f=\$16$.
- The function $f(t) = \begin{cases}10 &0\leq t<2\\20&2\leq t\leq 5\end{cases}$ models the price of the stock for the 5-day period. The graph below shows both the function $f$ and the average stock price $\bar f$. Show that the area under $f$ for $0\leq t\leq 5$ is 80. Then show that the area under $\bar f$ for $0\leq t\leq 5$ is also 80.
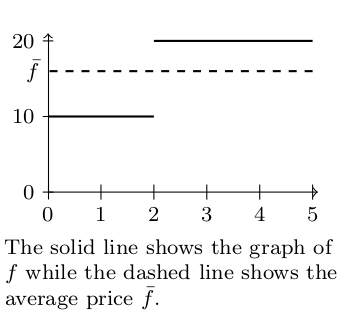
- The average value of a function over an interval $ [a,b] $ is a constant value $\bar f$ so that the areas under both $f$ and $\bar f$ are equal, which means $\ds\int_a^b \bar f dx = \int_a^b f dx.$ Solve for $\bar f$ to show that $$\bar f = \dfrac{\ds\int_a^b f dx}{\ds\int_a^b dx}.$$
Let's examine one last averaging question, this time as it relates to a rover. If we know the mass and center-of-mass of each part of the rover, we can use weighted averages to combine these values and obtain the center-of-mass of the the entire rover.
- Consider a simplified rover with a bottom and a top.
- The bottom part of the rover has a volume of $V_1$ m$^3$, a constant density (mass per volume) of $\delta_1$ g/m$^3$, and a center-of-mass located at $(\bar x_1,\bar y_1,\bar z_1)$.
- The top part of the rover has a volume of $V_2$ m$^3$, a constant density (mass per volume) of $\delta_2$ g/m$^3$, and a center-of-mass located at $(\bar x_2,\bar y_2,\bar z_2)$.
- Give the masses $m_1$ and $m_2$ of the bottom and top of the rover. Explain.
- What proportion of the total mass comes from the bottom of the rover?
- Explain why the center-of-mass of the entire rover is $$\left(\frac{\bar x_1(m_1)+\bar x_2(m_2)}{m_1+m_2},\frac{\bar y_1(m_1)+\bar y_2(m_2)}{m_1+m_2}, \frac{\bar z_1(m_1)+\bar z_2(m_2)}{m_1+m_2}\right) .$$
- The rover picks up an additional object. The object's mass is $m_3$ with center-of-mass $(\bar x_3, \bar y_3, \bar z_3)$. Modify the formula above to give the center-of-mass of the rover, together with the new object. Try writing the formula using summation notation.
Task 26.2
To find the mass of a thin metal plate occupying a region $R$ in the $xy$-plane, we add up the little masses (differentials) $dm = \delta(x,y)dA$, where $\delta$ is the density (mass per area), to obtain the mass as $$m=\iint_R\delta(x,y)dA = \iint_R\delta(x,y) dxdy= \iint_R\delta(x,y) dydx. $$ Note that if $\delta(x,y)=1$, then this reduces to the formula for the area of $R$. This task has you practice setting up area and mass integrals.
For each region $R$ below, draw the region. Then set up an iterated double integral which would give the area of the region. Then use the density provided to set up an iterated double integral that would give the mass of a metal plate occupying this region with the given density. You do not need to compute each integral, rather just set it up.
- The region $R$ is above the line $x+y=1$ and inside the circle $x^2+y^2=1$. The density is $\delta(x,y)=x$.
- The region $R$ is below the line $y=8$, above the curve $y=x^2$, and to the right of the $y$-axis. The density is $\delta(x,y)=xy^2$.
- The region $R$ is bounded by $2x+y=3$, $y=x$, and $x=0$. The density is $\delta(x,y)=7$.
Task 26.3
Consider the change-of-coordinates $x=r\cos \theta$ and $y=r\sin\theta$.
- The lines $r=1,r=2,r=3$ and $\theta=0,\theta=\frac{\pi}{6},\theta=\frac{\pi}{3}$ correspond to circles and lines in the $xy$ plane. Draw these circles and lines in the $xy$-plane.
- The box in the $r\theta$ plane with $2\leq r\leq 3$ and $\frac{\pi}{6}\leq \theta\leq \frac{\pi}{3}$ corresponds to a region in the $xy$ plane. Shade this region in the $xy$ plane.
- Let $(r,\theta)$ be an arbitrary point. Our goal is to develop a formula for the area of the region $R$ in the $xy$ plane where the radius ranges from $r$ to $r+dr$ and the angle ranges from $\theta$ to $\theta +d\theta$, shown in the diagram below.
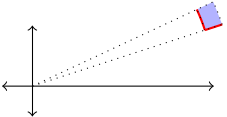
- Add the labels $r$, $\theta$, $dr$, $d\theta$, $r+dr$, and $\theta +d\theta$ to appropriate places in your diagram.
- The shaded region is approximately a rectangle. Letting the width of the rectangle be $dr$, explain why the height of the rectangle can be approximated by $rd\theta$. This means that a little area is give by $dA=rdrd\theta$.
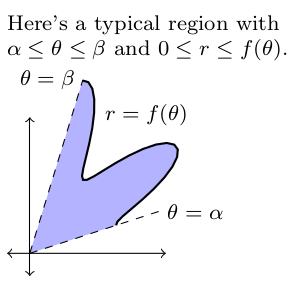
- Consider the region $R$ in the $xy$ plane bounded by $\alpha\leq \theta\leq \beta$ and $0\leq r\leq f(\theta)$ (shown below). The area of such a region $R$ in the $xy$ plane is the double integral $A=\int\int_R dA$. Explain why the area of the region in the $xy$ plane, when using polar coordinates, is $$A=\int_\alpha^\beta\int_0^{f(\theta)} rdrd\theta.$$
- Now consider the region $R$ bounded by $\alpha\leq \theta\leq \beta$ and $r_1(\theta)\leq r\leq r_2(\theta)$. Set up a double integral that would give the area of this region $R$.

Task 26.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
Day 26 - In class
Brain Gains (Rapid Recall, Jivin' Generation)

Draw a bear in polar coordinates, and then Cartesian coordinates.
- Draw a bear in polar coordinates, and then Cartesian coordinates.....
- Two objects lie on the $x$-axis. The first object has a mass of 2 kg and is located at the point $x=-1$ (or rather its center of mass is at that point). The second object has a mass of 3 kg and is located at the point $x=4$. Find the center-of-mass of the combined system.
Solution
The center of mass should be close to 4 than -1, because there is more mass there. There are many ways to do this problem. One way involves thinking of the 2kg object as 2 single kg objects, and the 3 kg object as 3 single kg objects. This means there are 5 equally weighted objects. We then average the $x$ coordinates of the 4 objects to get $$\bar x = \frac{(-1)+(-1)+4+4+4}{5} = \frac{(-1)2+(4)3}{2+3} = \frac{10}{5}=2.$$ Note that $\bar x = 2$ is closer to 4 than -1, as expected.

- If we travel $2\pi$ units along the outer edge of a disc of radius 6 units, then through what central angle, in radians, did we traverse?
Solution
The definition of radian measure is given by $$\text{radian measure} = \frac{\text{arc length}}{\text{radius of circle}}\quad \text{or}\quad \theta = \frac{s}{r}.$$ We've traveled (arc length) $s=2\pi$ units along a circle with radius $r=6$. The radian measure is $$\theta = \frac{s}{r} = \frac{2\pi}{6} = \frac{\pi}{3}.$$
Note that $s = r\theta$. In particular, note that if the angle we traverse is a little angle $d\theta$, then the little distance traveled is $$ds = rd\theta.$$
- Compute the polar double integral $\ds \int_0^{2\pi}\int_{0}^{7} r\, dr d\theta$.
Solution
With Mathematica, we can quickly get the answer using either of the following. Notice the order for bounds.
Integrate[Integrate[r, {r, 0, 7}], {theta, 0, 2 Pi}]
Integrate[r, {theta, 0, 2 Pi}, {r, 0, 7}]
By hand, we compute $$\ds \int_0^{2\pi}\int_{0}^{7} r\, dr d\theta = \int_0^{2\pi}\frac{r^2}{2}\bigg|_0^{7} d\theta = \int_0^{2\pi}\frac{7^2}{2} d\theta = \frac{7^2}{2}\theta\bigg|_0^{2\pi} = \pi7^2. $$ This shows that that area inside a circle of radius $7$ is $\pi 7^2$. Changing the 7 to an an arbitrary radius $a$, the above work shows that the area inside a circle of radius $a$ is $\pi a^2$.
- Set up a double integral formula that gives the area of the region in the first quadrant of the $xy$-plane that lies both inside the curve $r=2-2\cos\theta$ and inside the curve $r=2\cos\theta$.
Solution
We can use Mathematica to quickly plot the curves.
PolarPlot[2 - 2 Cos[t], {t, 0, Pi/2}]
PolarPlot[2 Cos[t], {t, 0, Pi/2}]
PolarPlot[{2 - 2 Cos[t], 2 Cos[t]}, {t, 0, Pi/2}]
Notice that rays starting from the origin, and heading out to the curves, hit the cardioid for $0\leq \theta\leq \pi/3$, and then swap to hitting the circle for $\pi/3\leq \theta\leq \pi/2$. This means we'll need two different integrals. One solution is $$ \int_{0}^{\pi/3}\int_{0}^{2-2\cos\theta} r dr d\theta + \int_{\pi/3}^{\pi/2}\int_{0}^{2\cos\theta} r dr d\theta. $$
- Draw the region whose volume is given by the triple integral $\ds\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-y}dzdydx.$
Solution
You end up with a pyramid, with a square base on the xz plane. Here's a solution with Mathematica.
ContourPlot3D[{x == 0, x == 1, y == 0, y == 1 - x, z == 0, z == 1 - y}, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}]
RegionPlot3D[x >= 0 && x <= 1 && y >= 0 && y <= 1 - x && z >= 0 && z <= 1 - y, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}]
- Compute the triple integral $\ds\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-y}dzdydx.$
Solution
The solution is 1/3, and I'll jump straight to Mathematica to compute it. The first option focus on the iterated nature of the integral. The later option is streamlined.
Integrate[Integrate[Integrate[1, {z, 0, 1 - y}], {y, 0, 1 - x}], {x, 0, 1}]
Integrate[1, {x, 0, 1}, {y, 0, 1 - x}, {z, 0, 1 - y}]
Group Problems
- Two objects lie on the $z$-axis. The first object has a mass of 2 kg and is located at the point $z=3$ (or rather its center of mass is at that point). The second object has a mass of 4 kg, and after being placed on top of the first object, its center-of-mass is located at the point $z=6$. Find the center-of-mass of the combined system.
- A box lies inside the rectangle $ [-2,6]\times [1,5] $ (so $-2\leq x\leq 6$ and $1\leq y \leq 5$ ).
- What is the center-of-mass $(\bar x,\bar y)$ of the rectangle? (Where is the geometric center?)
- Compute the integral formula $\ds\frac{\int_{-2}^{6}\int_1^5 x dydx}{\int_{-2}^{6}\int_1^5 1 dydx}.$ [Check: 64/32=2. This gives $\bar x$. ]
- Compute the integral formula $\ds\frac{\int_{-2}^{6}\int_1^5 y dydx}{\int_{-2}^{6}\int_1^5 1 dydx}.$ [Check: 96/32=3. This gives $\bar y$. ]
- Compute the integral formula $\ds\frac{\int_1^5 \int_{-2}^{6}x dxdy}{\int_1^5 \int_{-2}^{6}1 dxdy}$, to verify that swapping the order of integration still yields $\bar x = 2$.
- Draw the region described by the bounds of each integral.
- $\ds\int_{0}^{2}\int_{2x}^{4}dydx$
- $\ds\int_{0}^{4}\int_{0}^{y/2}dxdy$
- $\ds\int_{0}^{3\pi/2}\int_{0}^{2+2\cos\theta}rdrd\theta$
- $\ds\int_{-3}^{3}\int_{0}^{9-x^2}\int_{0}^{5}dzdydx$
- $\ds\int_{0}^{1}\int_{0}^{1-z}\int_{0}^{\sqrt{1-x^2}}dydxdz$
Here's 2 options for plotting the first region in Mathematica.
ContourPlot[{x == 0, x == 2, y == 2 x, y == 4}, {x, -1, 3}, {y, -1, 5}]
RegionPlot[ x >= 0 && x <= 2 && y >= 2 x && y <= 4, {x, -1, 3}, {y, -1, 5}]
Here's two options for the first 3D plot in Mathematica.
ContourPlot3D[{x == -3, x == 3, y == 0, y == 9 - x^2, z == 0, z == 5}, {x, -4, 4}, {y, -1, 10}, {z, -1, 6}]
RegionPlot3D[x >= -3 && x <= 3 && y >= 0 && y <= 9 - x^2 && z >= 0 && z <= 5, {x, -4, 4}, {y, -1, 10}, {z, -1, 6}]
- Set up an integral formula to compute each of the following:
- The mass of a disc that lies inside the circle $x^2+y^2=9$ and has density function given by $\delta = x+10$
- The $x$-coordinate of the center of mass (so $\bar x$) of the disc above.
- The $z$-coordinate of the center-of-mass (so $\bar z$) of the solid object in the first octant (all variables positive) that lies under the plane $2x+3y+6z=6$.
- The $y$-coordinate of the center-of-mass (so $\bar y$) of the same object.
Day 27 - Prep
Task 27.1
We can think of any object (such as a rover) as consisting of many little parts. Each little part contributes a little mass $dm$ and a center-of-mass. We can predict these quantities prior to building the rover, before we can weigh anything. We just need the length $ds$, area $dA$, or volume $dV$ of a small part, together with the material's density $\delta$ (mass per length, area, or volume, as appropriate).
- For thin wires, we get little masses $dm$ by multiplying little lengths $ds$ by a density $\delta$ with units of mass per length.
- For thin plates, we get little masses $dm$ by multiplying little areas $dA$ by a density $\delta$ with units of mass per area.
- For solid objects, we get little masses $dm$ by multiplying little volumes $dV$ by a density $\delta$ with units of mass per volume.
In all three cases, we can obtain the total mass $m$ by adding up the little masses with an integral. The difference between the three cases will be whether we use a single, double, or triple integral. Often the density $\delta$ will be constant throughout an entire object. However, composite materials exist where density $\delta (x,y,z)$ can vary throughout an object. We can then compute the center-of-mass using the average value formula.
Consider a thin rod (like a drive shaft or thinner) that lies along the $z$-axis for $a\leq z\leq b$.
- Suppose first that the rod is made out of a single material whose density is given by the constant $\delta$ g/m (mass per length).
- A small part of the rod has length $dz$. Compute $\int_a^b dz$, and explain what physical quantity this integral computes.
- A small bit of the rod has mass $dm = \delta dz$. Compute the total mass by computing $\int_a^b \delta dz$. Remember that $\delta$ is a constant.
- Guess the location of the average $z$-value of the rod (the center-of-mass).
- To validate your guess, compute and simplify the average value integral formula $$\bar z = \frac{\ds\int_a^b z dm}{\ds\int_a^b dm} = \frac{\ds\int_a^b z \delta dz}{\ds\int_a^b \delta dz}.$$
- Now suppose the rod is more like an antenna and the rod gets thinner as we move up the rod. This means the density $\delta(z)$ is now a function of $z$. Let's use, for simplicity, the linear density function $\delta(z)=b-z$.
- What is the density of the rod at $a$? What is the density of the rod at $b$? Construct a rough sketch of a rod that could have this type of density function.
- A small bit of the rod has mass $dm = \delta(z) dz$. Compute the total mass by computing $\int_a^b \delta(z) dz = \int_a^b (b-z)dz$.
- Is the location of $\bar z$ closer to $z=a$ or $z=b$? Explain.
- Find the $z$-coordinate of the center-of-mass by computing $$\bar z = \frac{\ds\int_a^b z dm}{\ds\int_a^b dm} = \frac{\ds\int_a^b z \delta dz}{\ds\int_a^b \delta dz}.$$ Feel free to use software. Verify that $\bar z = \frac{2a+b}{3}$.
Above we performed computations for a rod that lies on an axis. This works great for a drive shaft, or antenna, or any part of the rover that consists of a straight thin rod. But we can repeate these computations for a portion of the rover that is a thin flat plate, such as a solar panel, an armored plate, or any object which is best described by thinking of the area.
- Consider the triangular region $R$ in the first quadrant that lies under the line $\ds\frac{x}{a}+\frac{y}{b}=1$. If you would rather work with numbers instead of variables, feel free to let $a=5$ and $b=7$ in this problem.
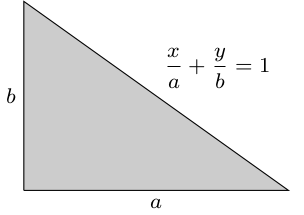
- Compute the double integral $\ds\int_0^a\int_0^{b(1-\frac{x}{a})} dy dx$. What physical quantity of the region $R$ does this integral give?
- The density of the metal plate is $\delta$ g/m$^2$. Set up a double integral formula to compute the mass of the region using this density.
- The center-of-mass in the $x$-direction is given by the formula $$\bar x = \frac{\ds\iint_R xdm}{\ds\iint_R dm}= \frac{\ds\int_0^a\int_0^{b(1-\frac{x}{a})} x \delta dy dx}{\ds\int_0^a\int_0^{b(1-\frac{x}{a})} \delta dy dx}.$$ Assuming $\delta$ is constant, compute this integral and show that $\bar x = \frac{a}{3}$. Feel free to use software.
- Set up an integral formula, like the one above, to compute $\bar y$. Show the integral formula you used, and then state the value $\bar y$ obtained.
Task 27.2
- Consider the region $R$ in the $xy$-plane that is below the line $y=x+2$, above the line $y=2$, and left of the line $x=5$. We can describe this region by saying for each $x$ with $0\leq x\leq 5$, we want $y$ to satisfy $2\leq y\leq x+2$. In set builder notation, we write $$R=\{(x,y)\in \mathbb{R}^2\mid 0\leq x\leq 5, 2\leq y\leq x+2\}.$$ We use the symbols $\{$ and $\}$ to enclose sets and the symbol $\mid$ for "such that". We read the above line as "$R$ equals the set of $(x,y)$ in the plane such that zero is less than $x$ which is less than 5, and 2 is less than $y$ which is less than $x+2$." The iterated double integral $\int_0^5\int_2^{x+2} dy dx$ gives the area of this region.
- Draw this region.
- Describe the region $R$ by saying for each $y$ with $c\leq y\leq d$, we want $x$ to satisfy $a(y)\leq x\leq b(y)$. In other words, find constants $c$ and $d$, and functions $a(y)$ and $b(y)$, so that for each $y$ between $c$ and $d$, the $x$ values must be between the functions $a(y)$ and $b(y)$. Write your answer using the set builder notation $$R=\{(x,y)\ | \ c\leq y\leq d, a(y)\leq x\leq b(y)\}.$$
- Finish setting up the iterated double integral $\int_?^?\int_?^? dx dy$.
- Compute both $\int_0^5\int_2^{x+2} dy dx$ and $\int_?^?\int_?^? dx dy$ (the integral you just set up), and verify that they give the same value.
- Consider the iterated integral $\ds \int_0^3\int_x^3 e^{y^2}dydx$. We could think of the function $e^{y^2}$ as a density, but notice that this function is independent of the region described by the bounds of the integral.
- Write the bounds as two inequalities ($0\leq x\leq 3$ and $?\leq y\leq ?$). Then draw and shade the region $R$ described by these two inequalities.
- Swap the order of integration from $dydx$ to $dxdy$. This forces you to describe the region using two inequalities of the form $c\leq y\leq d$ and $a(y)\leq x\leq b(y)$, obtaining the iterated double integral $\ds \int_?^?\int_?^? e^{y^2}dxdy$.
- Use your new bounds to compute the integral by hand.
- Why is the original integral $\ds \int_0^3\int_x^3 e^{y^2}dydx$ impossible to compute without first swapping the order of integration [Hint: Try computing the inner integral $\int_x^3 e^{y^2}dy$ -- why can't you? What does Mathematica give if you try to compute this inner integral?]
Task 27.3
I won't add another task. Work on the previous tasks, and come ready to discuss them.
Task 27.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |

