Day 24 - Prep

Learning Target Checkoff

A learning target quiz will appear in I-Learn. Complete and submit the quiz before the due date.

Day 24 - In class

There is no class. Complete the quiz in I-Learn.

Day 25 - Prep

We are beginning a new unit on integration.

Task 25.1

We need to become adept at describing regions in the plane, using inequalities. For this first task, we'll start with inequalities and from them shade a region in the plane.

  1. Shade the region in the $xy$-plane that satisfies the inequalities $-1\leq x\leq 1$ and $1-x\leq y\leq 4-x^2$.
  2. Shade the region in the $xy$-plane that satisfies the inequalities $-3\leq y\leq 0$ and $0\leq x\leq \sqrt{9-y^2}$.
  3. Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $0\leq \theta\leq \pi$ and $1\leq r\leq 3$.
  4. Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $-\frac{\pi}{6}\leq \theta \leq \frac{\pi}{6}$ and $0\leq r\leq 4\cos 3\theta$.
  5. Shade the region in the $xy$-plane that satisfies the polar coordinate inequalities $0\leq \theta\leq \frac{3\pi}{2}$ and $1\leq r\leq 3+2\cos\theta$.

We can also describe solid regions in space, using 3 sets of inequalities.

  1. Draw the region in space that satisfies the inequalities $0\leq x\leq 3$, $-1\leq y\leq 1$, and $0\leq z\leq 1-y^2$.
  2. Draw the region in space that satisfies the inequalities $-1\leq x\leq 1$, $0\leq y\leq 1-x^2$, and $0\leq z\leq 1-y$.
A look towards the future.

We will soon see that the area of the first region is given by the iterated double integral $\ds\int_{x=-1}^{x=1}\left(\int_{y=1-x}^{y=4-x^2}dy\right) dx$, written more compactly as $\ds\int_{-1}^{1}\int_{1-x}^{4-x^2}dy dx.$ The area of the second region is given by $\ds\int_{-3}^{0}\int_{0}^{\sqrt{9-y^2}}dx dy.$

The polar regions have areas given by the iterated double integrals $\ds\int_{0}^{\pi}\int_{1}^{3}rdr d\theta$, $\ds\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\int_{0}^{4\cos 3\theta}rdr d\theta$, and $\ds\int_{0}^{\frac{3\pi}{2}}\int_{1}^{3+2\cos\theta}rdr d\theta$.

The regions in space have a volume given by the iterated triple integrals $\ds\int_{0}^{3}\int_{-1}^{1}\int_{0}^{1-y^2}dz dy dx$ and $\ds\int_{-1}^{1}\int_{0}^{1-x^2}\int_{0}^{1-y}dz dy dx$.

Task 25.2

One way to compute the area of a region $R$ is overlay the region with a rectangular grid, where $dx$ and $dy$ are the distances between the vertical and horizontal lines of the grid. To find the area of the region, we first determine which of the rectangles contains a portion of the region $R$, and then add up the areas of of all such rectangles. This will overestimate the area, but we can then use limits to shrink both $dx$ and $dy$ to zero to obtain the area.

Consider the polar curve $r=1+\cos\theta$. We will use the approach described above to estimate the area of region $R$ that is inside this polar curve. We'll assume that all distances are given in meters. The bounds for each graph below are $-1\leq x\leq 2$ and $-2\leq y\leq 2$.

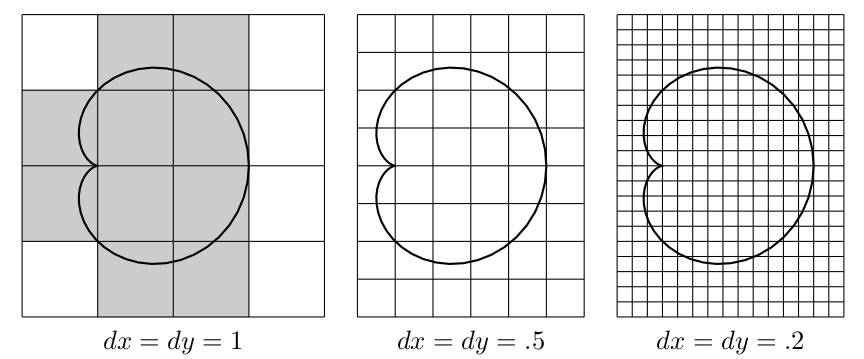
  1. For the first picture above, there are 10 rectangles (shaded) that contain a portion of the region $R$. Each of these rectangles has area $dA=dxdy=(1)(1) = 1 $, which means an overestimate for the area of $R$ is $A\approx 10 \, dA = 10(1)=10$. Describe a way to use these same rectangles to get an underestimate for the area of $R$.
  2. Now use the middle picture above (where $dx=dy=.5$) to shade and then count the number of rectangles that contain a portion of $R$. What is the area $dA$ of each little rectangle. Finish by giving an estimate for $A$.
  3. Now use the last picture with $dx=dy=.2$ to estimate the area of $R$.
  4. How can we obtain the exact value for the area of $R$?
  5. The questions above help focus on finding area, because each rectangle was given the same importance in the overall sum. Suppose instead that an object is made in the shape of the cardioid, but the portion that lies above the $x$-axis has a density of 2 kg/m^2, while the portion below has a density of 3 kg/m^2. How would you modify your work above to give an estimate for the mass (in kg)?

Task 25.3

In this task, we'll focus on the integrals $\int_C dx$ and $\int_C dy$, and from them develop a way to compute area using iterated (repeated) integrals.

  1. Consider the portion of the ellipse parametrized by $\vec r(t) = (3\cos t, 4\sin t)$ for $0\leq t\leq \pi/2$. Notice that parametrization starts at $(3,0)$ and ends at $(0,4)$. The integral $\int_C dx$ literally says ``Sum up little changes in $x$.'' Adding up little changes in $x$ gives the total change in $x$.
    • Differentials gives us $dx = -3\sin t dt$. Compute $\ds\int_C dx=\int_{t=0}^{t=\pi/2}dx = \ds\int_{t=0}^{t=\pi/2}-3\sin t dt$ and verify that it gives the total change in $x$ from $t=0$ to $t=\pi/2$.
    • Guess the value of $\ds\int_{t=0}^{t=\pi/2}dy$ (the integral adds up what?), and then check your solution.
  2. Consider the region $R$ between the functions $y=x^2$ and $y=-x$ for $0\leq x\leq 3$. Our goal is to explain why the iterated integral $\ds\int_{x=0}^{x=3}\left(\int_{y=-x}^{y=x^2} dy \right)dx$ gives the area of the region $R$.
    • Draw both functions and shade the region $R$.
    • Compute the integral $\ds\int_{y=-x}^{y=x^2}dy$ for arbitrary $x$. This integral comutes, for a given value of $x$, the total change in $y$ (so a height).
    • Recall that $dx$ is a small width. When we multiply the previous integral by this width $dx$, we will obtain the area of a small rectangular region whose height is given by $\ds\int_{y=-x}^{y=x^2}dy$ and width is given by $dx$. Pick a value $x$ between 0 and 3, and then construct a picture that illustrates this rectangular region whose area is given by $dA=\ds\left(\int_{y=-x}^{y=x^2} dy \right)dx$.
    • Explain why $\ds\int_{x=0}^{x=3}\left(\int_{y=-x}^{y=x^2} dy \right)dx$ gives the area of the region $R$.
  3. Consider the double integral $$\int_{y=-1}^{y=2}\left(\int_{x=y^2}^{x=y+2}dx\right)dy.$$
    • The bounds in the integral above describe a region in $xy$ plane where $-1\leq y\leq 2$ and $y^2\leq x\leq y+2$. Sketch this region.
    • Consider the inner integral $\int_{x=y^2}^{x=y+2}dx$. This integral adds up changes in $x$, so gives a total change in $x$ (hence a width). Add to your sketch several line segments whose widths are given by this integral.
    • When we multiply a width $\int_{x=y^2}^{x=y+2}dx$ by a small height $dy$, we get a little bit of area $dA$. Pick a value $y$ between $-1$ and $2$, and then at that height draw a small rectangle whose area is given by $dA = \left(\int_{x=y^2}^{x=y+2}dx\right) dy$.
    • Adding up little bits of area gives total area, so the double integral $$\int_{y=-1}^{y=2}\left(\int_{x=y^2}^{x=y+2}dx\right)dy$$ gives an area. Compute the integral.

Task 25.4

Pick some problems related to the topics we are discussing from the Text Book Practice page.


Today

« October 2022 »

Sun

Mon

Tue

Wed

Thu

Fri

Sat

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31