- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
We still have some tasks from Day 20 to finish discussing in class.
Day 20 - Prep
Task 20.1
Consider the function $f(x,y)=x^3-3x+y^2-4y$.
- Find the critical points of $f$ by finding when $Df(x,y)$ is the zero matrix.
- Find the eigenvalues of $D^2f$ at any critical points. [Hint: First compute $D^2f$. Since there are two critical points, evaluate the second derivative at each point to obtain 2 different matrices. Then find the eigenvalues of each matrix.]
- Label each critical point as a local maximum, local minimum, or saddle point, and state the value of $f$ at the critical point.
- Use Mathematica to construct a 2D contour plot and 3D surface plot of the function to visually verify that your solution is correct. Choose bounds for your plots so that the critical points are clearly visible.
The Mathematica Notebook 2ndDerTest.nb can help you check much of your work above.
Task 20.2
Let's now return to a Lagrange multiplier problem, where we have a constraint that limits the values over which we want to optimize a function. Consider the curve $xy^2=54$.
- Start by drawing the curve.
The distance from each point on this curve to the origin is a function that must have a minimum value. We will find a point $(a,b)$ on the curve that is closest to the origin.
The first step to any Lagrange multiplier problem is to identify the function $f(x,y)$ that we wish to maximize or minimize, and then then identify the constraint and write it in the form $g(x,y) = c$. The distance from $(x,y)$ to the origin is $f(x,y) = \sqrt{(x-0)^2+(y-2)^2}=\sqrt{x^2+y^2}.$ This is the function we wish to minimize. The square root on this function will complicate computations later on. Because the square root function is increasing, note that $h(x,y) = x^2+y^2$ will have its minimum value at the same place. Because of this, we can simplify our work and use $f(x,y)=x^2+y^2$ as the function we wish to minimize.
- What's the constant $c$ and function $g$ so that our constraint can be written in the form $g(x,y)=c$?
- Solve the system $\vec \nabla f = \lambda \vec \nabla g$ and $g=c$.
- After computing the gradients, state the 3 equations that form the system we must solve, and then solve it.
- Note that in this problem, the number $\lambda$ is not an eigenvalue, rather it is a multiplier that helps us know if $\vec \nabla f$ and $\vec \nabla g$ lie on the same line (are parallel or antiparallel, i.e. "Is one gradient a multiple of the other?".
- State the $(x,y)$ coordinates on the curve $xy^2=54$ that are closest to the origin.
Remember that you can use LagrangeMultipliers.nb to check your work.
- How does the problem above change if we want to find the point on the curve that is closest to $(3,4)$? Solving the corresponding system of equations by hand will not be simple, but we can use the Mathematica notebook above to quickly answer this question, once we state $f$, $g$, and $c$. You will need to numerically approximate the solution that Mathematica gives (type //N at the end of a line of code to numerically approximate the output). The solution is $(x,y) = (3.11122,4.16612)$.
Task 20.3
Consider the function $f(x,y,z) = -x^2+y^2+z^2$.
- Start by using the ContourPlot3D[] command in Mathematica to draw several level surface of this function. You can use the Mathematica notebook ContourSurfaceGradient.nb to help you.
The level surface which passes through the point $(3,2,-1)$ is shown below, along with the tangent plane to the surface through the point $(3,2,-1)$. This surface is called a hyperboloid of two sheets.
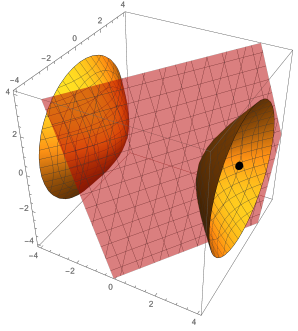
- Use the differential $$df = f_xdx+f_ydy+f_zdz \quad\text{or}\quad df=\vec\nabla f(a,b,c)\cdot(dx,dy,dz) . $$ to give an equation of the tangent plane to this surface at the point $(3,2,-1)$. [Hint: Start by explaining why $df=0$. Then we have $dx=x-3$, $dy=y-?$, and $dz =?$. Don't forget to evaluate the partials at the correct point.]
- Suppose the function $f(x,y,z) = -x^2+y^2+z^2$ gives the temperature (in Celcius) at points in space near some object (located at the origin), with $x,y,z$ values given in meters. Compute the temperature at $(3,2,-1)$, and then use differentials to approximate the temperature at $(3.01,1.98, -0.98)$. [What are $dx$, $dy$, and $dz$?]
- Compute the directional derivative of $f(x,y,z) = -x^2+y^2+z^2$ at the point $(3,2,-1)$ in the direction $(1, -2, 2)$. What are the units of $D_{ (1, -2, 2) }f(3,2,-1)$?
- What similarities, and what differences, do you see in the three questions above?
Task 20.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
Day 21 - Prep
Task 21.1
Let $f(x,y) = 9-x^2-y^2$. Rather than using Cartesian coordinates to examine this function, we could instead use polar coordinates $x=r\cos \theta$ and $y=r\sin\theta$.
- Compute the differential $df$ in terms of $x$, $y$, $dx$, and $dy$.
- Compute the differentials $dx$ and $dy$ in terms of $r$, $\theta$, $dr$, and $d\theta$.
- Use substitution to obtain $df$ in terms of $r$, $\theta$, $dr$, and $d\theta$. Write your answer as the linear combination $df = (?)dr + (?)d\theta$.
- State $\frac{\partial f}{\partial r}$ and $\frac{\partial f}{\partial \theta}$.
- We can write the change of coordinates as the function $(x,y) = \vec T(r,\theta) = (r\cos\theta, r\sin\theta)$. Given a polar coordinate $(r,\theta)$, the function $\vec T$ returns the Cartesian (rectangular) coordinate $(x,y)$. Compute $f(\vec T(r,\theta))$.
- Compute the differential $d\vec T$ and write is as the linear combination $d\vec T = (?)dr + (?)d\theta$. Note that the questions marks will be vectors, not numbers, because the function $\vec T$ returns a vector (not a number).
- State the total derivatives $Df(x,y)$ and $D\vec T(r,\theta)$. How would you interpret $Df(\vec T(r,\theta))$.
- Compute the matrix product $Df(\vec T(r,\theta))D\vec T(r,\theta)$. [Hint: the partial derivatives you computed earlier should appear.]
Task 21.2
This task will have you practice using the second derivative test to locate maxima, minima, and/or saddle points for function $f(x,y)$ of two variables.
- Consider the function $f(x,y)=x^3-3x+y^2-4y$.
- Find the critical points of $f$ by finding when $Df(x,y)$ is the zero matrix.
- Find the eigenvalues of $D^2f$ at any critical points. [Hint: First compute $D^2f$. Since there are two critical points, evaluate the second derivative at each point to obtain 2 different matrices. Then find the eigenvalues of each matrix.]
- Label each critical point as a local maximum, local minimum, or saddle point, and state the value of $f$ at the critical point.
- Consider the function $f(x,y) = 6x^2-2x^3+3y^2+6xy$. The function has two critical points $(0,0)$ and $(1,-1)$. At each of these points, evaluate the second derivative and then find the corresponding eigenvalues. Use these eigenvalues to classify each critical point as the location of a local maximum, local minimum, or saddle point.
The Mathematica Notebook 2ndDerTest.nb can help you check much of your work above.
Task 21.3
To use Lagrange Multipliers, we must (1) identify the function $f(x,y)$ to be optimized along with the constant $c$ and function $g$ in the constraint $g(x,y)=c$, (2) write the system of equations that results from $\vec \nabla f = \lambda \vec \nabla g$ and $g(x,y)=c$, (3) solve this system, and (4) determine which points correspond to maxes and which to mins. The third step, solving a system of equations, can become extremely difficult quite quickly, but luckily modern software can help facilitate this part of the process. Please use the Mathematica notebook LagrangeMultipliers.nb to help you check your work and visual what you're doing in this task.
- Let $f(x,y) = 20 x + 2 y^2$. Use Lagrange multipliers to identify the location of any extreme values of $f$ along the line $100=4x+8y$. Complete this by hand, and then check your work with software.
- A rover travels along a circle of radius 5, centered at the origin. The elevation of the surrounding hill is give by $z = 4x^2-4xy+y^2$. What are the highest and lowest elevations reached by the rover? [If the system to solve is brutal, then use software to help you.]
Task 21.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
Day 21 - In class
Brain Gains (Rapid Recall, Jivin' Generation)

- Consider the function $$x^3 - y^3 - 12 x + 3 y - 4.$$
- Compute the directional derivative of the function at the point $(1,2)$ in the direction $(3,4)$.
- Give an equation of the tangent plane to the function at the point $(1,2, f(1,2))$.
- Give an equation of the tangent line to the level curve that passes through the function at the point $(1,2)$.
- Locate all critical points of the function.
- One critical point is $(2,1)$. Use the eigenvalues of $D^2f(2,1)$ to classify this critical point as a maximum, minimum, or saddle point. We'll use software to examine the other 3 points.
- Consider the function $w(x,y)$, where $x$ and $y$ both depend on $r$ and $h$. Compute $\frac{\partial w}{\partial r}$.
- Let $f(x,y)=x^2+y$, and $g(x,y)=4x+3y$. Find the locations of all local maxima and minima of $f$ on the curve $g(x,y) = 12$. In other words, solve the system $\vec \nabla f = \lambda \vec \nabla g$ and $g(x,y)=12$.
Solution
We have $\vec \nabla f = (2x,1)$ and $\vec \nabla g = (4,3)$. The equation $\vec \nabla f = \lambda \vec \nabla g$ gives us $2x=\lambda\cdot 4$ and $1 = \lambda 3$. The second equation tells us $\lambda =1/3$, and the first equation tells us $x=\lambda\cdot 2=2/3$. Substitution into $4x+3y=12$ tells us $y=(12-8/3)/3$.
Group Problems
- For the function $f(x,y)=x^2+4xy+3y^2-10x-18y$, verify that the first derivative $Df(x,y)$ and second derivative $D^2f(x,y)$ are $$Df(x,y) = \begin{bmatrix}2x+4y-10&4x+6y-18\end{bmatrix}\quad\text{and}\quad
D^2f(x,y) = \begin{bmatrix}\begin{matrix}2\\4\end{matrix}&\begin{matrix}4\\6\end{matrix}\end{bmatrix}.
$$
- Solve $Df(x,y)=\begin{bmatrix}0&0\end{bmatrix}$, to find the critical points of this function. [Check: $(x,y)=(3,1)$.]
- Find the eigenvalues of $D^2f(3,1)$. [Check: $\lambda = 4\pm\sqrt{20} = 4\pm 2\sqrt{5}$.]
- Does the function $f$ have a local max, local min, or saddle at $(3,1)$? Explain.
- Consider the function $f(x,y,z) = 3xy+z^2$. We'll be analyzing the level surface that passes through the point $P=(1,-3,2)$.
- Compute the differential $df$, and then evaluate the differential at $P$.
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1$, $dy=y-(-3)$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- What relationship exists between the gradient of $f$ at $P$ and the tangent plane through $P$?
- Suppose a plane passes through the point $(a,b,c)$ and has normal vector $(A,B,C)$. Give an equation of that plane.
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$.
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$.
- Suppose $h$ is a function of $p$ and $q$, where $p$ and $q$ are both functions of $x$, $y$, and $z$. Compute the partial derivatives of $h$ with respect to $x$, $y$, and $z$.
Day 22 - Prep
Task 22.1
There are three optimization problems below. Each can be solved with a different method (first semester calculus, Lagrange multipliers, and the second derivative test with eigenvalues). Solve each problem below, and explain your choice of the method used.
- The elevation near a rover is given by $z=y+x^2$. The rover travels along a path given by $y-2x=5$. Find the $(x,y)$ location of any maxes or mins along the rover's path, and classify the point(s) appropriately.
- The elevation near a rover is given by $z=y+x^2$. The rover travels along the path parametrized by $\vec r(t) =(t,2t+5)$. Find the $(x,y)$ location of any maxes or mins along the rover's path, and classify the point(s) appropriately.
- The elevation near a rover is given by $f(x,y)=x^2+xy+y^2-2y$. Determine the location of any maxes or mins near the rover, and classify the point(s) appropriately.
Task 22.2
For each problem below, decide if you'll need to use Lagrange multipliers or the second derivative test. If you choose Lagrange multipliers, then state $f$, $g$, and $c$, along with the system of equations that must be solved. If you choose the second derivative test, then state $f$, $Df$, and $D^2f$. Then use the appropriate Mathematica notebook (either LagrangeMultipliers.nb or 2ndDerTest.nb) to solve the problem.
- Let $f(x,y)=x^3 + 3xy +y^3$. Find all local extreme values of $f$.
- Find the dimensions of the rectangle of largest possible area that will fit inside of the ellipse $\frac{x^2}{9}+\frac{y^2}{25}=1$.
- Find three numbers whose sum is 9 and whose sum of squares is minimized.
- Find the largest box in the first octant (all variables are positive) that can fit under the paraboloid $z=9-x^2-y^2$. The volume of such a box is given by $V=lwh = xyz = xy(9-x^2-y^2)$.
- A rover travels along a circle of radius 5, centered at the origin. The elevation of the surrounding hill is give by $z = 4x^2-4xy+y^2$. What are the highest and lowest elevations reached by the rover.
Task 22.3
In this task we'll derive the version of the second derivative test that is found in most multivariate calculus texts. The test given below only works for functions of the form $f:\mathbb{R}^2\to\mathbb{R}$. The eigenvalue test you have been practicing will work with a function of the form $f:\mathbb{R}^n\to\mathbb{R}$, for any natural number $n$.
Suppose that $f(x,y)$ has a critical point at $(a,b)$.
- We know that $D^2f(a,b) = \begin{bmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{bmatrix}$, where all partials are evaluated at $(a,b)$. Prove that the eigenvalues of $D^2f(a,b)$ are given by $$\lambda = \frac{(f_{xx}+f_{yy})\pm \sqrt{(f_{xx}+f_{yy})^2 - 4(f_{xx}f_{yy}-f_{xy}^2)}}{2}.$$
- Let $D=f_{xx}f_{yy}-f_{xy}^2$.
- If $D<0$, explain why the eigenvalues differ in sign.
- If $D=0$, explain why zero is an eigenvalue.
- If $D>0$, explain why the eigenvalues must have the same sign.
- If $D>0$, and $f_{xx}>0$, explain why $f$ has a local minimum at $(a,b)$.
- If $D>0$, and $f_{xx}<0$, explain why $f$ has a local maximum at $(a,b)$.
- How would you interpret $f_{xx}$ in terms of concavity?
- The only critical point of $f(x,y) = x^2+3xy+2y^2$ is at $(0,0)$. Does this point correspond to a local maximum, local minimum, or saddle point? Find $D$ from part 2 to answer the question.
Task 22.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
