- I-Learn, Class Pictures, Learning Targets, Text Book Practice
- Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus
We still have some tasks from Day 18 to finish discussing in class.
Day 18 - Prep
Task 18.1
In first semester calculus, differential notation is $dy=f' dx$. At $x=c$, the tangent line passes through the point $P=(c,f(c))$. If $Q=(x,y)$ is any other point on the line, then the vector $\vec {PQ} = (x-c,y-f(c))$ tells us that when $dx=x-c$ we have $dy=y-f(c)$. Substitution give us an equation for the tangent line tangent line as $$\underbrace{y-f(c)}_{dy}={f'(c)}\underbrace{(x-c)}_{dx}.$$ This equation tells us that a change in the output ($y-f(c)$) equals the derivative times a change in the input ($x-c$). In this task, we'll repeat this process to obtain an equation of a tangent plane to a function $f(x,y)$, where differential notation gives $$dz = \frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy.$$
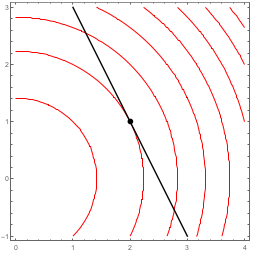
Consider the function $z=f(x,y)=9-x^2-y^2$. We'll be finding an equation of the tangent plane to $f$ at $(x,y)=(2,1)$. Here is surface plot along with the tangent plane at $(2,1,f(2,1))$, together with a contour plot.
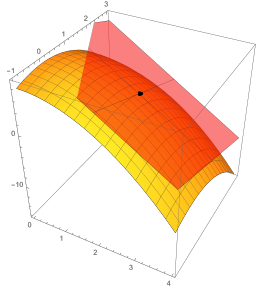
- Compute the partial derivatives $f_x$ and $f_y$, and the differential $dz$. At the point $(x,y) = (2,1)$, evaluate the partial derivatives and the function $z=f(x,y)$.
- One point on the tangent plane to the surface at $(2,1)$ is the point $P=(2,1,f(2,1))$. Let $Q=(x,y,z)$ be another point on this plane. Use the vector $\vec{PQ}$ to obtain $dz$ when $dx = x-2$ and $dy = y-1$.
- We'd like an equation of the tangent plane to $f(x,y)$ when $x=2$ and $y=1$. Differential notation tells us that $$\underbrace{z-?}_{dz}=(-4)\underbrace{(x-?)}_{dx}+(?)\underbrace{(y-?)}_{dy}.$$ Fill in the blanks to get an equation of the tangent plane.
- Rewrite the equation you got in the form $A(x-a)+B(y-b)+C(z-c)=0$ and state a normal vector to the plane.
- The level curve of $f$ that passes through $(2,1)$ has no change in height, so $dz=0$. Use this fact to give an equation of the tangent line to this level curve at $(2,1)$.
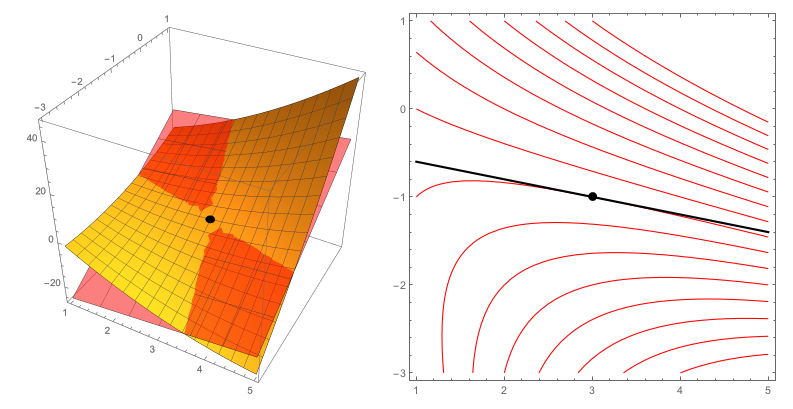
Now let $z=f(x,y)=x^2+4xy+y^2$. At the point $P=(x,y)=(3,-1)$, we'll give an equation of the tangent plane to the surface and an equation of the tangent line to the level curve of $f$ that passes through this point.
- Give an equation of the tangent plane at $P=(x,y)=(3,-1)$. [Hint: Find $f_x$, $f_y$, $dx$, $dy$, and then $dz$, all at $(x,y)=(3,-1)$. Then substitute, as done above.]
- The level curve of $f$ that passes through $P$ is a curve in the plane. Give an equation of the tangent line to this curve at $P$. [Hint: Since we're on a level curve, what does $dz$ equal? The equation is almost identical to the previous part, with one minor change based on what $dz$ equals.]
The tangent plane and tangent line you just found are shown below.
Task 18.2
A rover moves on a hill where elevation is given by $z=f(x,y)=9-x^2-y^2$. The rover's path is parametrized by $\vec r(t)=(2\cos t, 3\sin t)$.
- At time $t=0$, what is the rover's position $\vec r(0)$, and what is the elevation $f(\vec r(0))$ at that position? Then find the positions and elevations at $t=\pi/2$, $t=\pi$, and $t=3\pi/2$ as well.
- In the plane, draw the rover's path for $t\in [0,2\pi]$. Then, on the same 2D graph, include a contour plot of the elevation function $f$. Include the level curves that pass through the points in part 1. Along each level curve drawn, state the elevation of the curve. [If you end up with an ellipse and several concentric circles, then you've done this right.]
- As the rover follows its elliptical path, the elevation is rising and falling. At which $t$ does the elevation reach a maximum? A minimum? Explain, using your graph.
- As the rover moves past the point at $t=\pi/4$, is the elevation increasing or decreasing? In other words, is $\dfrac{df}{dt}$ positive or negative? Use your graph to explain.
Notice above that we wanted $\frac{df}{dt}$, the rate of change of elevation with respect to time, even though the function $f(x,y)$ does not explicitly have $t$ as an input. The proper notation would be $\frac{d(f\circ r)}{dt}$, but this is so cumbersome that it's generally avoided. The notation $\frac{df}{dt}$ requires the reader to infer from context that $x$ and $y$ depend on $t$.
- At the point $\vec r(t)$, we'd like a formula for the elevation $f(\vec r(t))$. What is the elevation of the rover at any time $t$? [In $f(x,y)$, replace $x$ and $y$ with what they are in terms of $t$.]
- Compute $df/dt$ (the derivative as you did in first-semester calculus).
Let's repeat the above, but first compute differentials before substitution. For reference, we let $f(x,y)=9-x^2-y^2$ and $(x,y)=\vec r(t)=(2\cos t, 3\sin t)$.
- Compute the differential $df$ in terms of $x$, $y$, $dx$, and $dy$.
- Compute $dx$ and $dy$ in terms of $t$ and $dt$.
- Use substitution to write $df$ in terms of $t$ and $dt$. Then divide by $dt$ to obtain $\frac{df}{dt}$. Did you get the same answer as the previous part?
- Use your work above to state both $\vec\nabla f(x,y)$ and $\frac{d\vec r}{dt}$. Show that $\frac{df}{dt} = \vec\nabla f(x,y)\cdot \frac{d\vec r}{dt}$.
Task 18.3
A second-order partial derivative of $f$ is a partial derivative of one of the partial derivatives of $f$. The second-order partial of $f$ with respect to $x$ and then $y$ is the quantity $\frac{\partial}{\partial y}\left[\frac{\partial f}{\partial x}\right]$, so we first compute the partial of $f$ with respect to $x$, and then compute the partial of the result with respect to $y$. Alternate notations exist, for example the same second-order partial above we can write as $$\frac{\partial}{\partial y}\left[\frac{\partial f}{\partial x}\right]=\left(f_{x}\right)_y=f_{xy}=\ds\frac{\partial}{\partial y}\frac{\partial}{\partial x}f = \frac{\partial}{\partial y}\frac{\partial f}{\partial x} = \frac{\partial^2 f}{\partial y \partial x}.$$ The subscript notation $f_{xy}$ is easiest to write. Sometimes we'll use subscript notation to mean something other than a partial derivative (like the $x$ or $y$ component of a vector), at which point we use the fractional partial derivative notation to avoid confusion.
Consider the functions $f(x,y,z) = xy^2z^3$ and $g(x,y)=x\cos(xy)$.
- First compute $\vec \nabla f$. Then compute $f_{xy}$ and $\frac{\partial^2 f}{\partial z\partial y}$. Explain how you got these. End by computing the entire second derivative $D\vec\nabla f(x,y,z)$ (it is a 3 by 3 matrix with all 9 second partials placed inside).
- Compute $g_x$ and then $g_{xy}$. Then compute $g_y$ followed by $g_{yx}$.
- Now let $f(x,y)=3xy^3+e^{x}.$ Compute the four second partials $$\ds \frac{\partial^2 f}{ \partial x^2},\quad \ds\frac{\partial^2 f}{\partial y \partial x},\quad \ds\frac{\partial^2 f}{\partial y^2}, \quad \text{ and }\ds\frac{\partial^2 f}{\partial x \partial y}.$$
- For $f(x,y)=x^2\sin(y)+y^3$, compute both $f_{xy}$ and $f_{yx}$.
- Make a conjecture about a relationship between $f_{xy}$ and $f_{yx}$. Then use your conjecture to quickly compute $f_{xy}$ if $$f(x,y)=3xy^2+\tan^{2}(\cos(x)) (x^{49}+x)^{1000}.$$
Task 18.4
The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below.
- Return to any of the previous day's OpenStax problems to locate extra practice.
Day 19 - Prep
Task 19.1
In the first calculus books, there was no mention of the chain rule. This is because differentials were extremely common notation, and the chain rule, when working with differentials, is simply substitution. In this task, we'll develop some rules for how to compute derivatives when functions depend on other functions (so composite functions).
- Suppose that $f(x,y,z) = ax+by+cz$, and $x=mt$, $y=nt$, and $z = pt$, for some constants $a,b,c,m,n,p$. Compute the differentials $df$, $dx$, $dy$, and $dz$. Then use substitution to obtain the differential of $f$ in terms of $t$ and $dt$. Finish by stating $\frac{df}{dt}$.
- Suppose now that $g$ is a function of $x$ and $y$, but $x$ and $y$ are functions of $u$, $v$, and $w$. This means, by definition of the differential and partial derivatives, that $dg = g_xdx+g_ydy$, along with $dx = x_udu+x_vdv+x_wdw$ and $dy = y_udu+y_vdv+y_wdw$. Substitution gives $$\begin{align*} dg &= g_xdx+g_ydy\\ &= g_x(x_udu+x_vdv+x_wdw)+g_y(y_udu+y_vdv+y_wdw)\\ &= (?)du+(?)dv+ (?)dw. \end{align*}$$ Fill in the question marks above, and then use your answer to state the three partials $\dfrac{\partial g}{\partial u}$, $g_v$, and $D_w g$.
- Consider the function $h(x,y,z)$, where $x$, $y$, and $z$ are functions of $r$ and $\theta$. State the differentials of $h$, $x$, $y$, and $z$, and then use substitution to prove that $$\dfrac{\partial h}{\partial r} = \dfrac{\partial h}{\partial x}\dfrac{\partial x}{\partial r} +\dfrac{\partial h}{\partial y}\dfrac{\partial y}{\partial r} +\dfrac{\partial h}{\partial z}\dfrac{\partial z}{\partial r}.$$ Obtain a similar formula for $\dfrac{\partial h}{\partial \theta}$.
Feel free to ask me in class how this relates to matrix multiplication.
Task 19.2
Suppose a rover travels around the circle $g(x,y)=x^2+y^2=1$. The elevation of the surrounding terrain is $f(x,y) = x^2+y+4$. The plot below shows the rover's path (the constraint $g(x,y)=1$), placed on the same grid as a contour plot of the elevation (the function $f(x,y)$ we wish to optimize).
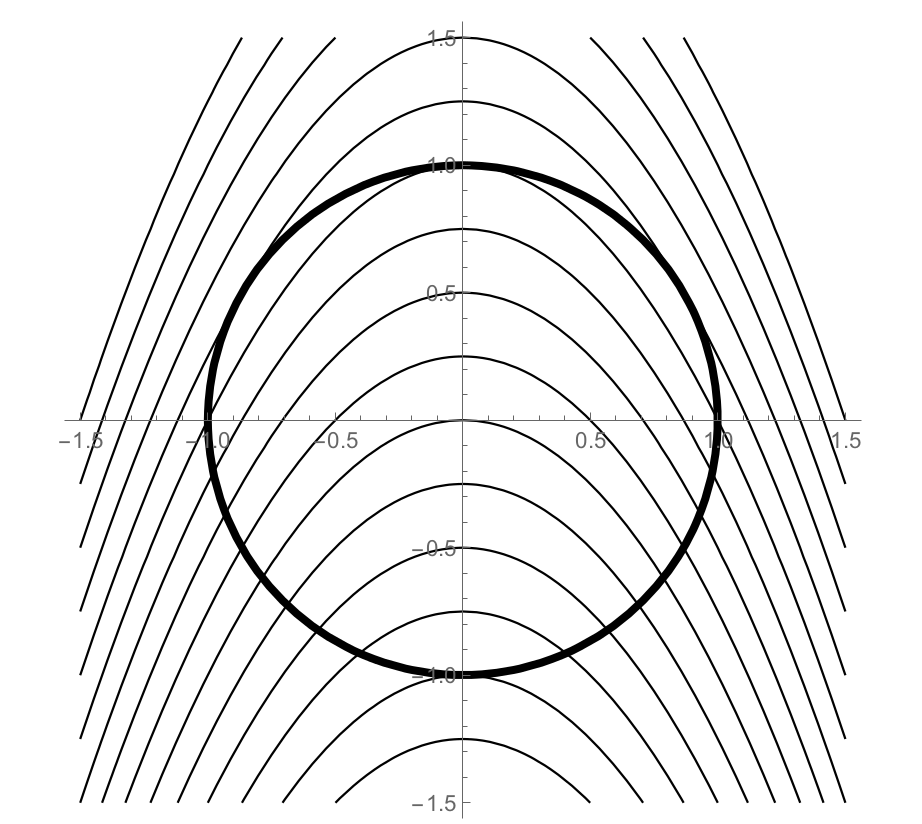
Each level curve above represents a difference in elevation of 0.25 m. Our goal is to find the maximum and minimum elevation reached by the rover as it travels around the circle. We will optimize $f(x,y)$ subject to the constraint $g(x,y)=1$.
- Label each level curve with its elevation. Print this page, or copy the curves down on your paper.
- At which $(x,y)$ point does the rover encounter the minimum elevation? What is the minimum elevation? Explain, using the plot.
- Suppose the rover is currently at the point $(0,1)$ on its circular path. As the rover moves left, will the elevation rise or fall? What if the rover moves right? Is $(0,1)$ the location of a local maximum or local minimum?
- On your graph, place a dot(s) where the rover reaches a maximum elevation. What is the maximum elevation? Explain.
- Rather than visually inspecting level curves, let's examine the gradients $\vec \nabla f$ and $\vec \nabla g$ to see how these gradients compare at maximums and minimums.
- On the graph above, draw $\vec \nabla f$ at lots of places on your contour plot.
- At lots of points on the circle, with a different color, draw $\vec \nabla g$.
- Make sure you draw both gradients at all the points corresponding to local maxes and mins.
- At the local maximums and minimums, Lagrange noticed that $\vec \nabla f = \lambda \vec \nabla g$.
- How would you interpret the equation $\vec \nabla f = \lambda \vec \nabla g$?
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- Explain why the system of equations $\vec \nabla f = \lambda \vec \nabla g$ and $g(x,y)=c$ is equivalent to the system of equations $$2x = \lambda 2x,\quad 1=\lambda 2y,\quad x^2+y^2=1.$$
- Solve the system of equations above to obtain 4 ordered pairs $(x,y)$. You can use the Mathematica notebook LagrangeMultipliers.nb to check your work.
- At each ordered pair, find the elevation. What is the maximum elevation obtained, and where does it occur? What is the minimum elevation obtained, and where does it occur?
Suppose $f$ and $g$ are continuously differentiable functions. Suppose that we want to find the maximum and minimum values of $f(x,y)$ subject to the constraint $g(x,y)=c$ (where $c$ is some constant). If a local maximum or minimum occurs, it must occur at a spot where the gradient of $f$ and the gradient of $g$ point in the same, or opposite, directions. This means the gradient of $g$ must be a multiple of the gradient of $f$. To find the $(x,y)$ locations of the maximum and minimum values (if they exist), we solve the system of equations that result from $$\vec \nabla f = \lambda \vec \nabla g,\quad \text{and}\quad g(x,y)=c$$ where $\lambda$ is the proportionality constant. The locations of maximum and minimum values of $f$ will be among the solutions of this system of equations.
Task 19.3
This task will mostly involve reading through some definitions and an example, with a short example at the end.
Let $A$ be a square matrix, as $A=\begin{bmatrix} \begin{pmatrix}a\\b\end{pmatrix}& \begin{pmatrix}c\\d\end{pmatrix}\end{bmatrix} = \begin{bmatrix}a&c\\b&d\end{bmatrix}$. The eigenvalues $\lambda$ and eigenvectors $\vec x$ of $A$ are solutions $\lambda$ and $\vec x\neq \vec 0$ to the equation $A\vec x=\lambda \vec x$, effectively replacing the matrix product (linear combination) with scalar multiplication.
The identity matrix $I$ is a square matrix with 1's on the diagonal and zeros everywhere else, so in 2D we have $I = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}$. To find the eigenvalues, we rewrite $A\vec x = \lambda\vec x$ in the form $A\vec x -\lambda\vec x=\vec 0$ or $A\vec x -\lambda I \vec x=\vec 0$, which becomes $(A-\lambda I) =\vec 0.$ We need to find the values $\lambda$ so that $\left(\begin{bmatrix} a&c\\b&d\end{bmatrix}-\lambda \begin{bmatrix} 1&0\\0&1 \end{bmatrix} \right)\begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}0\\0\end{pmatrix} \quad\text{or}\quad \begin{bmatrix} a-\lambda &c\\b&d-\lambda \end{bmatrix}\begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}0\\0\end{pmatrix}.$ A linear algebra course will show that $\lambda$ satisfies $$(a-\lambda)(d-\lambda)-bc=0.$$
Let $f(x,y)$ be a function so that all the second partial derivatives exist and are continuous. The second derivative of $f$, written $D^2f$ and sometimes called the Hessian of $f$, is a square matrix. Suppose $P=(a,b)$ is a critical point of $f$, meaning $\vec\nabla f(a,b) = (0,0)$.
- Suppose all the eigenvalues of $D^2f(a,b)$ are positive. Then at all points $(x,y)$ sufficiently near $P$, the gradient $\vec \nabla f(x,y)$ points away from $P$. The function has a local minimum at $P$.
- Suppose all the eigenvalues of $D^2f(a,b)$ are negative. Then at all points $(x,y)$ sufficiently near $P$, the gradient $\vec \nabla f(x,y)$ points inwards towards $P$. The function has a local maximum at $P$.
- Suppose the eigenvalues of $D^2f(a,b)$ differ in sign. Then at some points $(x,y)$ near $P$, the gradient $\vec \nabla f(x,y)$ points inwards towards $P$. However, at other points $(x,y)$ near $P$, the gradient $\vec \nabla f(x,y)$ points away from $P$. The function has a saddle point at $P$.
- If the largest or smallest eigenvalue of $f$ equals 0, then the second derivative tests yields no information.
Let's look at an example. Consider $f(x,y)=x^2-2x+xy+y^2$. The gradient is $\vec \nabla f(x,y)=(2x-2+y,x+2y)$. The critical points of $f$ occur where the gradient is zero. We need to solve the system $2x-2+y=0$ and $x+2y=0$, which is equivalent to solving $2x+y=2$ and $x+2y=0$. Double the second equation, and then subtract it from the first to obtain $0x-3y=2$, or $y=-2/3$. The second equation says that $x=-2y$, or that $x=4/3$. So the only critical point is $(4/3,-2/3)$.
The second derivatives is $ D^2f = \begin{bmatrix}2&1 \\1&2\end{bmatrix}.$ The second derivative is constant, so $D^2 f(4/3,-2/3)$ is the same as $D^2f(x,y)$. (In general, the critical point may affect your matrix.) To find the eigenvalues we solve $$(2-\lambda)(2-\lambda)-(1)(1)=0.$$ Expanding the left hand side gives $4-4\lambda + \lambda^2 -1 = 0$. Simplifying and factoring gives us $\lambda^2-4\lambda +3 = (\lambda-3)(\lambda -1) = 0$. The eigenvalues are $\lambda = 1$ and $\lambda=3$. Since both numbers are positive, we know the gradient points outwards away from the critical point. The critical point $(4/3,-2/3)$ corresponds to a local minimum of the function. The local minimum is the output $f(4/3,-2/3) = (4/3)^2-2(4/3)+(4/3)(-2/3)+(-2/3)^2$.
Let's try this process on our own. Consider the function $f(x,y)=x^2+4xy+y^2$.
- Find the critical points of $f$ by finding when $Df(x,y)$ is the zero matrix.
- Find the eigenvalues of $D^2f$ at any critical points.
- Label each critical point as a local maximum, local minimum, or saddle point, and state the value of $f$ at the critical point.
Task 19.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
Day 19 - In class
Brain Gains (Rapid Recall, Jivin' Generation)

- Let $f(x,y)=ax+by$ and $\vec r(t) = (ct+d, et+f)$. Compute $\frac{df}{dt}$.
Solution
Two options:
- Substitute, so $f(\vec r(t)) = a(ct+d)+b(et+f)$, and then differentiate.
- Compute differentials, so $df=adx+bdy$, $dx=cdt$, and $dy=edt$, and then substitute.
Either way, we end up with $$\dfrac{df}{dt} = ac+be.$$ Symbolically, we have $$\frac{df}{dt} = \underbrace{a}_{f_x}\underbrace{c}_{\frac{dx}{dt}}+\underbrace{b}_{f_y}\underbrace{e}_{\frac{dy}{dt}} = f_x\frac{dx}{dt}+f_y\frac{dy}{dt}. $$ We call this the chain rule.
- The hyperbola $x^2-y^2=5$ passes through the point $(3,2)$. Differentials tell us $2xdx-2ydy = 0$. Give an equation of the tangent line to this curve at $(3,2)$.
Solution
Let $(x,y)$ be a point on the tangent line.
- The change in $x$ along the tangent line from $(3,2)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,2)$ to $(x,y)$ is $dy=y-2$.
- Plugging $x=3$, $y=2$, $dx=x-3$ and $dy=y-2$ into the differential $2xdx-2ydy = 0$ gives the desired equation as $$2(\underbrace{3}_{x})\underbrace{ (x-3) }_{dx}-2(\underbrace{2}_{y})\underbrace{ (y-2) }_{dy} = 0.$$
- Let $f(x,y)=2x^2+4y$, and $g(x,y)=2x+y$. Solve the system $\vec \nabla f = \lambda \vec \nabla g$ together with $g(x,y)=3$.
Solution
We have $\vec \nabla f = (4x,4)$ and $\vec \nabla g = (2,1)$. The equation $\vec \nabla f = \lambda \vec \nabla g$ means $$(4x,4) = \lambda(2,1) = (2\lambda,1\lambda).$$ This gives us the two equations $4x=2\lambda$ and $4 = \lambda$. The second equation tells us $\lambda=4$. The first equation tells us $x=2\lambda/4 = 2$. Substitution of $x=2$ into $2x+y=3$ tells us $y=-1$.
- For the function $f(x,y) = 4x^2y+y^3$, compute $\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)$.
Solution
Since we know $\frac{\partial f}{\partial y} = 4x^2(1)+3y^2$, then we have $$\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) =\ds\frac{\partial}{\partial x}\left(4x^2(1)+3y^2\right) =8x. $$ We call the above the second partial derivative of f, first with respect to $y$, and then with respect to $x$. For this function $f(x,y)$, there are four total second partial derivatives of $f$, namely $$ f_{xx}=\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right), \quad f_{xy}=\ds\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right), \quad f_{yx}=\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right), \quad f_{yy}=\ds\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right). $$
- For the function $f(x,y) = 4x^2y+y^3$, compute the four second partial derivatives $f_{xx}$, $f_{xy}$, $f_{yx}$, and $f_{yy}$, and then state the second derivative $D^2f(x,y)$.
Solution
We have $f_x = 8xy$ which gives
- $f_{xx} = 8y$ and
- $f_{xy} = 8x$.
We have $f_y = 4x^2(1)+3y^2$ which gives
- $f_{yx} = 8x$ and
- $f_{yy} = 6y$.
The second derivative is $$D^2f(x,y) = \begin{bmatrix}f_{xx}&f_{yx}\\f_{xy}&f_{yy}\end{bmatrix} = \begin{bmatrix}8y&8x\\8x&6y\end{bmatrix}.$$
- The eigenvalues of the matrix $\begin{bmatrix}a&b\\c&d\end{bmatrix}$ are the solutions to the equation $(a-\lambda)(d-\lambda)-bc=0$. Find the eigenvalues of the matrix $\begin{bmatrix}5&3\\2&4\end{bmatrix}$.
Solution
We have $$(5-\lambda)(4-\lambda)-(2)(3) = \lambda^2-9\lambda+20-6 = \lambda^2-9\lambda-14 = (\lambda - 7)(\lambda - 2).$$ This equals zero when $\lambda = 7 $ or $\lambda =2$.
Finding the eigenvalues of a 2 by 2 matrix will always result in solving a quadratic equation. Carefully chosen problems will factor nicely, but in general the eigenvalues will not be integers.
Group Problems
- Find the eigenvalues of the following matrices (take turns).
- $\begin{bmatrix}2&4\\4&2\end{bmatrix}$, $\begin{bmatrix}2&3\\1&4\end{bmatrix}$, $\begin{bmatrix}1&6\\4&3\end{bmatrix}$, $\begin{bmatrix}3&2\\1&2\end{bmatrix}$.
- Check: 6,-2; 5,1; 7,-3; 4,1
- We will find the points on the curve $g(x,y)=xy^2=16$ that minimize the function $f(x,y)=x^2+y^2$.
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- To find the points where $\vec \nabla f$ and $\vec \nabla g$ are either parallel or anti-parallel, we need to solve $\vec \nabla f=\lambda\vec \nabla g$ together with $g(x,y) = 16$. Write the three equations that result from needing to solve this system (you should get $2x=\lambda y^2$, $2y = \lambda 2xy$, and $xy^2=16$.)
- Solve the system above for $x$ and $y$ (a value for $\lambda$ will appear, but we don't need it). [Check: $x=2$ and $y=\pm \sqrt{8}=\pm 2\sqrt{2}$, $\lambda = $ something. ]
- Consider the function $f(x,y)= 2x^2+3xy+4y^2-5x+2y$.
- Find all critical points of $f$, so find when the first derivative equals zero. [Check: $(x,y) = (2,-1)$.]
- Compute the second derivative $D^2f(x,y)$.
- Determine the eigenvalues of the second derivative at the critical point. [Check: The eigenvalues are $\lambda = 6\pm\sqrt{13}$, so $\lambda \approx 9.6$ or $\lambda \approx 2.4$.]
- Do we have a local max, local min, or saddle, at this critical point?
- Consider the function $f(x,y,z) = 4x^2+4y^2+z^2$. We'll be analyzing the surface at the point $P=(1/2,0,\sqrt{3})$.
- Compute the gradient $\vec\nabla f(x,y,z)$, and then give $\vec\nabla f(P)$.
- Compute the differential $df$, and then the differential at $P$. [Check: For the latter, $df = 4dx+0dy+2\sqrt{3}dz$]
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1/2$, $dy=y-0$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane to the surface.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$. [Check: $0=8(x-1)+16(y-2)-6(z+3)$.]
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
Day 20 - Prep
Task 20.1
Consider the function $f(x,y)=x^3-3x+y^2-4y$.
- Find the critical points of $f$ by finding when $Df(x,y)$ is the zero matrix.
- Find the eigenvalues of $D^2f$ at any critical points. [Hint: First compute $D^2f$. Since there are two critical points, evaluate the second derivative at each point to obtain 2 different matrices. Then find the eigenvalues of each matrix.]
- Label each critical point as a local maximum, local minimum, or saddle point, and state the value of $f$ at the critical point.
- Use Mathematica to construct a 2D contour plot and 3D surface plot of the function to visually verify that your solution is correct. Choose bounds for your plots so that the critical points are clearly visible.
The Mathematica Notebook 2ndDerTest.nb can help you check much of your work above.
Task 20.2
Let's now return to a Lagrange multiplier problem, where we have a constraint that limits the values over which we want to optimize a function. Consider the curve $xy^2=54$.
- Start by drawing the curve.
The distance from each point on this curve to the origin is a function that must have a minimum value. We will find a point $(a,b)$ on the curve that is closest to the origin.
The first step to any Lagrange multiplier problem is to identify the function $f(x,y)$ that we wish to maximize or minimize, and then then identify the constraint and write it in the form $g(x,y) = c$. The distance from $(x,y)$ to the origin is $f(x,y) = \sqrt{(x-0)^2+(y-2)^2}=\sqrt{x^2+y^2}.$ This is the function we wish to minimize. The square root on this function will complicate computations later on. Because the square root function is increasing, note that $h(x,y) = x^2+y^2$ will have its minimum value at the same place. Because of this, we can simplify our work and use $f(x,y)=x^2+y^2$ as the function we wish to minimize.
- What's the constant $c$ and function $g$ so that our constraint can be written in the form $g(x,y)=c$?
- Solve the system $\vec \nabla f = \lambda \vec \nabla g$ and $g=c$.
- After computing the gradients, state the 3 equations that form the system we must solve, and then solve it.
- Note that in this problem, the number $\lambda$ is not an eigenvalue, rather it is a multiplier that helps us know if $\vec \nabla f$ and $\vec \nabla g$ lie on the same line (are parallel or antiparallel, i.e. "Is one gradient a multiple of the other?".
- State the $(x,y)$ coordinates on the curve $xy^2=54$ that are closest to the origin.
Remember that you can use LagrangeMultipliers.nb to check your work.
- How does the problem above change if we want to find the point on the curve that is closest to $(3,4)$? Solving the corresponding system of equations by hand will not be simple, but we can use the Mathematica notebook above to quickly answer this question, once we state $f$, $g$, and $c$. You will need to numerically approximate the solution that Mathematica gives (type //N at the end of a line of code to numerically approximate the output). The solution is $(x,y) = (3.11122,4.16612)$.
Task 20.3
Consider the function $f(x,y,z) = -x^2+y^2+z^2$.
- Start by using the ContourPlot3D[] command in Mathematica to draw several level surface of this function. You can use the Mathematica notebook ContourSurfaceGradient.nb to help you.
The level surface which passes through the point $(3,2,-1)$ is shown below, along with the tangent plane to the surface through the point $(3,2,-1)$. This surface is called a hyperboloid of two sheets.
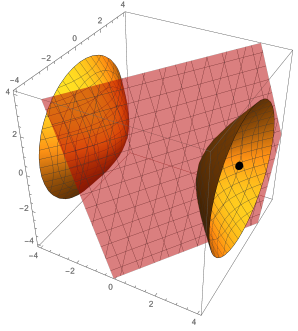
- Use the differential $$df = f_xdx+f_ydy+f_zdz \quad\text{or}\quad df=\vec\nabla f(a,b,c)\cdot(dx,dy,dz) . $$ to give an equation of the tangent plane to this surface at the point $(3,2,-1)$. [Hint: Start by explaining why $df=0$. Then we have $dx=x-3$, $dy=y-?$, and $dz =?$. Don't forget to evaluate the partials at the correct point.]
- Suppose the function $f(x,y,z) = -x^2+y^2+z^2$ gives the temperature (in Celcius) at points in space near some object (located at the origin), with $x,y,z$ values given in meters. Compute the temperature at $(3,2,-1)$, and then use differentials to approximate the temperature at $(3.01,1.98, -0.98)$. [What are $dx$, $dy$, and $dz$?]
- Compute the directional derivative of $f(x,y,z) = -x^2+y^2+z^2$ at the point $(3,2,-1)$ in the direction $(1, -2, 2)$. What are the units of $D_{ (1, -2, 2) }f(3,2,-1)$?
- What similarities, and what differences, do you see in the three questions above?
Task 20.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
