• I-Learn, Class Pictures, Learning Targets, Text Book Practice
• Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus

Day 12 - Prep

Task 12.1

A computer chip has been disconnected from electricity and sitting in cold storage for quite some time. The chip is connected to power, and a few moments later the temperature (in Celsius) at various points $(x,y)$ on the chip is measured. From these measurements, statistics is used to create a temperature function $z=f(x,y)$ to model the temperature at any point on the chip. Suppose that this chip's temperature function is given by the equation $z=f(x,y)=9-x^2-y^2$. (This could just as easily have been the elevation of a rover at a point $(x,y)$ on a hill.) We'll be creating both a 2D contour plot (topographical map) and 3D surface plot of this function in this task.

The points in the plane with temperature $f(x,y)=0$ satisfy $0=9-x^2-y^2$, or equivalently $x^2+y^2=9$. These points lie on a circle of radius 3, so we can draw that circle in the $xy$-plane (the start of our 2D contour plot) and also in 3D by plotting a circle of radius 3 at height $z=0$ (the start of our 3D surface plot). These two plots are shown below.

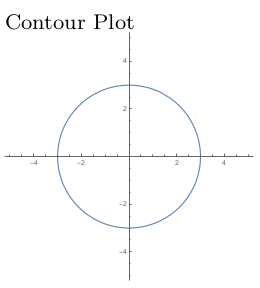
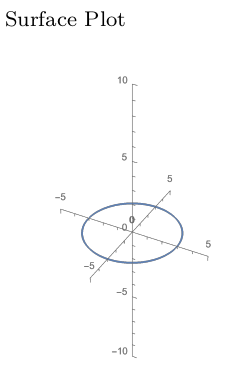
1. What is the temperature at $(0,0)$, $(1,2)$, and $(-4,3)$?
2. Which points in the plane have temperature $z=5$? Add this contour (level curve) to your 2D contour plot. Then at height $z=5$, add the same curve to the 3D surface plot.
3. Repeat the above for $z=8$, $z=9$, and $z=1$. What's wrong with letting $z=10$?
4. Letting $y = 0$ provides a vertical cross section of the surface. This is the curve $z = 9-x^2-0^2$. This curve cannot be drawn on the contour plot, but can be added to your 3D surface plot. Add that curve, and then add the curve given by letting $x=0$.
5. Describe the 3D surface that you created with your plot. Add any extra features to your 3D surface plot to convey the 3D image you constructed. You can use the Mathematica file ContourSurfaceGradient.nb to check your work.
6. For the function $f(x,y) = x^2-y$, construct a 2D contour plot and 3D surface plot.

Task 12.2

Suppose that an explosion occurs at the origin $(0,0,0)$. Heat from the explosion starts to radiate outwards. Suppose that a few moments after the explosion, the temperature at any point in space is given by $w=T(x,y,z)=100-x^2-y^2-z^2.$

1. Which points in space have a temperature of 99? To answer this, replace $T(x,y,z)$ by $99$ to get $99=100-x^2-y^2-z^2$. Use algebra to simplify this to $x^2+y^2+z^2=1$. Draw this object.
2. Which points in space have a temperature of 96? of 84? Draw the surfaces.
3. What is the temperature at $(3,0,-4)$? Draw the set of points that have this same temperature.
4. The 4 surfaces you drew above are called level surfaces. If you walk along a level surface, what happens to your temperature?
5. When we compute a level surface of a function $w = f(x,y,z)$, which variable do we make constant? When we compute a level curve of a function $z=f(x,y)$, which variable do we make constant?
6. Consider now the function $w=f(x,y,z)=x^2+z^2$. This function has an input $y$, but notice that changing the input $y$ does not change the output of the function.
   • Draw a graph of the level surface $w=4$. [When $y=0$ you can draw one curve. When $y=1$, you draw the same curve. When $y=2$, again you draw the same curve. This kind of graph we call a cylinder, and is important in manufacturing where you extrude an object through a hole.]
   • Graph the level surface $9=x^2+z^2$ (so $w=9$), and $w=16$.

You can use the Mathematica file ContourSurfaceGradient.nb to check your work.

Task 12.3

Suppose the elevation $z$ of terrain near a rover is given by the formula $z=f(x,y) = x^2+3xy$.

1. Suppose that $x$ and $y$ are both functions of $t$, and then use implicit differentiation to compute $\dfrac{dz}{dt}$. Write your answer in the form $$\frac{dz}{dt} = (?)\frac{dx}{dt}+(?)\frac{dy}{dt}.$$
2. The differential of $z$ (or differential of $f$ as $z=f(x,y)$) is obtained by multiplying both sides above by $dt$. Verify that $dz = (2x+3y)dx+3xdy$.
3. Write the differential of $f$ as the dot product $$df = (?,?)\cdot(dx,dy).$$

When we write the differential of a function $f(x,y)$ in the form $df = M dx +N dy$, we call $M$ the partial derivative of $f$ with respect to $x$, written $f_x$ or $\frac{\partial f}{\partial x}$ or $D_x f$, and we call $N$ the partial derivative of $f$ with respect to $y$, written $f_y$ or $\frac{\partial f}{\partial y}$ or $D_y f$. The vector $(f_x,f_y)$ we call the gradient of $f$, written as $\vec\nabla f$, which means the differential of $f$ is always $$df = \vec \nabla f \cdot (dx,dy) = (f_x, f_y)\cdot (dx,dy) = f_xdx+f_ydy.$$ Similar definitions hold for functions of more variables.

4. For the function $f(x,y)=3x^2+2xy$, compute the differential $df$ (in terms of $x$, $y$, $dx$, $dy$), the partial derivatives $f_x$ and $f_y$, and the gradient $\vec \nabla f(x,y)$.
5. For the function $g(r,s,t)=r^2s^3+4rt^2$ compute the differential $dg$ (in terms of $r$, $s$, $t$, $dr$, $ds$, $dt$), the partial derivatives $g_r$ and $\frac{\partial g}{\partial s}$ and $D_tg$, and the gradient $\vec \nabla g(r,s,t)$.

Task 12.4

The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below.

• section 4.1 exercises 14-29, 30-32, 39-41, 42-47, 48-52, 53-58

Day 12 - In class

Brain Gains (Rapid Recall, Jivin' Generation)

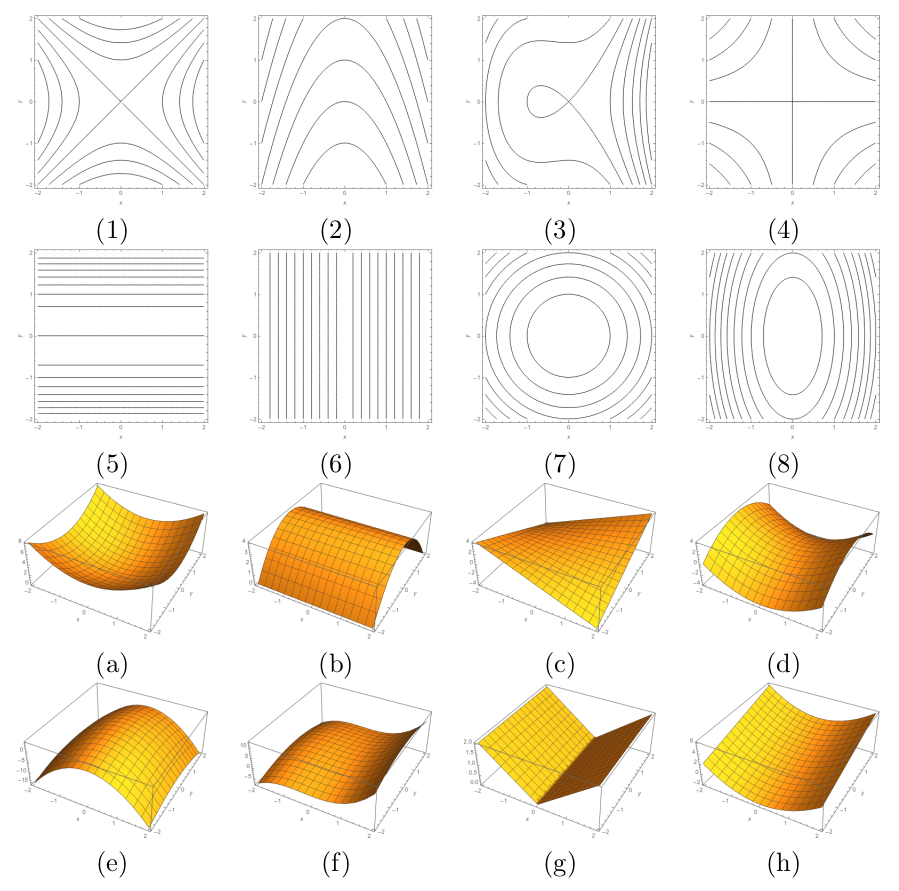
• Match the contour plots to the surface.

• For the function $f(x,y) = x^2-y^2$, graph the level curve that passes through the point $(1,0)$.
• Let $z= x^3+4xy$. We can think of this as an elevation function that tells us the height $z$ of a hill at a point $(x,y)$. Compute $dz$ in terms of $x$, $y$, $dx$, and $dy$.

• Write your answer above in the form $dz = (?_1) dx+(?_2) dy$.

• Write your answer above as the dot product of two vectors, namely $dz= (?????)\cdot (dx,dy)$.

• What is the gradient of $z$ for the function above, written $\vec \nabla z(x,y)$? We will often just write $\vec\nabla z$, when the input variables $x$ and $y$ are clear from context.

• What is the partial derivative of $z$ with respect to $x$, written $\ds\frac{\partial z}{\partial x}$ or $z_x$ or $D_x z$?

• What is the partial derivative of $z$ with respect to $y$, written $\ds\frac{\partial z}{\partial y}$ or $z_y$ or $D_y z$?

Group Problems

1. A rover is located on a hill whose elevation is given by $z=f(x,y) = 3x^2+2xy+4y^2$.
   • Compute the differential $dz$ in terms of $x$, $y$, $dx$, and $dy$, and write it in the form $dz=(?_1)dx+(?_2)dy.$
   • Write your answer above as the dot product of two vectors, i.e., $dz = (??, ??)\cdot(dx, dy).$
   • State the gradient of $f$, so $\vec \nabla f$.
   • State $\dfrac{\partial f}{\partial x}$ and $f_y$.
2. The sides of a rectangle $x=3$ ft and $y=2$ ft, with tolerances $dx = .1$ ft and $dy = 0.05$ ft. Use differentials to estimate the tolerance on the area $A=xy$ that results from the given tolerances on $x$ and $y$. So compute $dA$ and then plug in $x$, $y$, $dx$, $dy$, as given. [Check: $dA = 0.35.$]
3. Let $z = f(x,y) = x^2+y^2$.
   • Construct a 2D contour plot. (Let $z = 1$, and plot the resulting curve. Then let $z=4$ and plot the resulting curve. Repeat with various values for the output $z$.)
   • Construct a 3D surface plot.
   • Compute the gradient of $f$.
   • Note that the gradient of $f$ is a vector field. Graph the vector field on the same 2D plot as you did your contour plot.
4. Let $z = f(x,y) = 4-y^2$.
   • Construct a 2D contour plot.
   • Construct a 3D surface plot.
   • Compute the gradient of $f$.
   • Note that the gradient of $f$ is a vector field. Graph the vector field on the same 2D plot as you did your contour plot.

Day 13 - Prep

Task 13.1

For the function $f(x,y) = 9-x^2-y^2$, we can compute the differential $df = -2xdx-2ydy$, the partial derivatives $f_x = -2x$ and $f_y=-2y$, along with the gradient $\vec \nabla f(x,y) = (-2x,-2y)$. Notice that the gradient is a vector field, so at the point $(x,y)$ we can draw the vector $(-2x,-2y)$.

1. Construct a plot of the vector field $\vec \nabla f(x,y) = (-2x,-2y)$.
2. Add to your vector field plot a contour plot of $f(x,y) = 9-x^2-y^2$ (we constructed a contour plot for the function in a previous Task).
3. What relationships do you see between the vectors from the gradient plot, and the level curves from your contour plot.

For the function $f(x,y) = x^2-y$, we can compute the differential $df = 2xdx-1dy$, the partial derivatives $f_x = 2x$ and $f_y=-1$, along with the gradient $\vec \nabla f(x,y) = (2x,-1)$. Again, notice that the gradient is a vector field, so at the point $(x,y)$ we can draw the vector $(2x,-1)$.

4. Construct a plot of the vector field $\vec \nabla f(x,y) = (2x,-1)$.
5. Add to your vector field plot a contour plot of $f(x,y) = x^2-y$ (we constructed a contour plot for the function in a previous Task).
6. What relationships do you see between the vectors from the gradient plot, and the level curves from your contour plot.

You can use the Mathematica file ContourSurfaceGradient.nb to check your work.

Task 13.2

Suppose the Mars rover Curiosity is currently on a hill, and its position is at the center of the map on the left below. Zooming in on the rover's position yields the map on the right below (the color legend applies to the graph on the right).

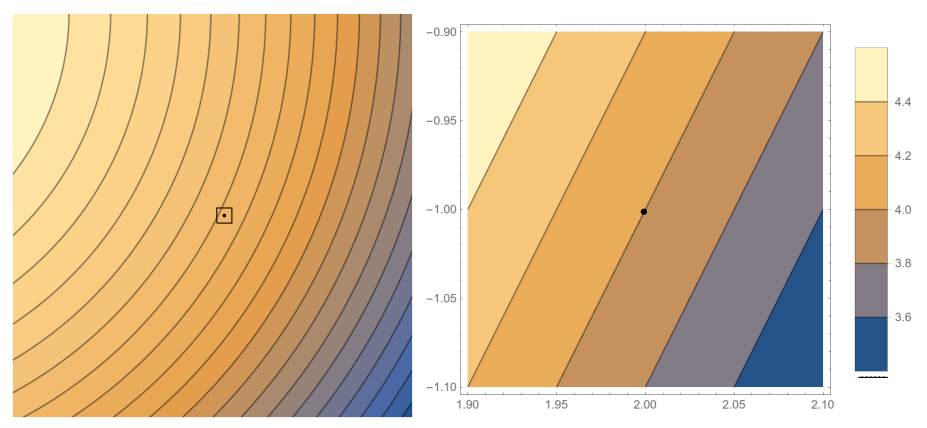
The contours in the graph to the right each represent a change in height of 0.2 units. The bounds for the graph are $1.9\leq x\leq 2.1$ and $-1.1\leq y\leq -0.9$. For simplicity of computations, let's assume the $x$, $y$ and $z$ axes use the same units. The rover is currently located at the point $(2,-1)$, shown as a dot.

The rover can head in many directions. In this problem we'll estimate the slope in several directions. For example, if the rover follows the vector $(0,1)$, heads north, then it has to move a distance (run) of $\Delta y = 0.1$ units to hit the next contour, resulting in a change in height of $\Delta z = +0.2$ units. This means the slope in the $(0,1)$ direction is $$\ds\frac{\text{rise}}{\text{run}} = \frac{\Delta z}{\text{distance moved in $xy$ plane}} = \frac{+0.2}{0.1} = 2.$$

1. Estimate the slope if the rover heads east, following $(1,0)$.
2. If the rover heads south, following $(0,-1)$, estimate the slope.
3. If the rover follows the direction $(1,1)$ (so northeast), what distance must the rover travel to hit the next contour? Use this to estimate the slope in the $(1,1)$ direction.
4. Estimate the slope in the $(1,2)$ direction.

Rather than starting with a contour plot and using it to visually estimate slopes, let's start with a function of the form $z=f(x,y)$ and use it to compute slopes. Suppose the elevation $z$ of terrain near the rover is given by the formula $z=f(x,y) = x^2+3xy$, and the rover is currently at $P=(2,-1)$.

5. Compute the differential $dz$ and write it in the form $dz = (?)dx+(?)dy$. Then evaluate $dz$ at the rover's location $P=(2,-1)$. [Check: Did you get $dz = (1)dx+(6)dy$?]
6. If the rover follows the direction $(dx,dy)$, explain why the slope is $\frac{dz}{\sqrt{(dx)^2+(dy)^2}}$.
7. Estimate the slope if the rover heads east, following $(dx,dy)=(1,0)$. Then estimate the slope if the rover heads north, following $(dx,dy)=(0,1)$. What do these values have to do with the partial derivatives of $f$?
8. Estimate the slope in the $(1,1)$ direction and then the $(1,2)$ direction.

Task 13.3

The volume of a right circular cylinder is $V(r,h)= \pi r^2 h$.

1. If we think of $h$ as a constant, so that $V(r)$ is only a function of $r$, then compute $\frac{dV}{dr}$.
2. If instead we think of $r$ as a constant, so that $V(h)$ is only a function of $h$, then compute $\frac{dV}{dh}$.
3. Compute the differential of $V(r,h)$, and then state the gradient $\vec \nabla V(r,h)$ along with the partial derivatives $\frac{\partial V}{\partial r}$ and $\frac{\partial V}{\partial h}$.
4. If we know $r=3$ and $h=4$, and we know that $r$ could increase by $dr=0.1$ and $h$ could increase by about $dh=0.2$, then use differentials to estimate how much $V$ will increase.

Notice that we were able to compute the partial derivatives above, without ever needing to compute the differential first. We obtain $\frac{\partial V}{\partial r}$ by imagining that every variable other than $r$ was a constant, and then computing the regular derivative.

5. The volume of a box is given by $f(x,y,z)=xyz$. Without computing the differential, compute $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, and $\frac{\partial f}{\partial z}$.
6. Now compute the differential $df$ (use implicit differentiation if needed) and verify that the partial derivatives you computed before actually show up in the differential $df$.
7. If the current measurements are $x=2$, $y=3$, and $z=5$, and we know that expected tolerances are $dx=.01$, $dy=.02$, and $dz=.03$, then estimate the change in volume.

Task 13.4

The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below.

• section 4.3, exercises 118-131

---

Today

« September 2022 »
Sun	Mon	Tue	Wed	Thu	Fri	Sat
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

• Sep24, Oct, Nov, Dec