I-Learn, Class Pictures, Learning Targets, Text Book Practice
Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus

Day 4 - Prep

Task 4.1

Consider the curve $\vec r(t) = (2t+3, 4(2t-1)^2)$.

Construct a graph of $\vec r$ for $0\leq t\leq 2$.
If this curve represents the path of a rover (meters for distance, minutes for time), find the velocity of the rover at any time $t$, and then specifically at $t=1$. What is the rover's speed at $t=1$?
Give a vector equation of the tangent line to $\vec r$ at $t=1$. Include this on your graph.
State the rover's acceleration vector.
Explain how to obtain the slope of the tangent line, and then write an equation of the tangent line using point-slope form. [Hint: How can you turn the direction vector, which involves $(dx/dt)$ and $(dy/dt)$, into the number given by the slope $(dy/dx)$?]

Task 4.2

We are ready to tackle the problem of finding the length of a path. This length we call arc length. If a rover moves at a constant speed, then the distance traveled is simply $$\text{distance} = \text{speed}\times\text{time}.$$ This requires that the speed be constant. What if the speed is not constant? Over a really small time interval $dt$, the speed is almost constant, so we can still use the idea above.

Suppose a rover (or other object) moves along the path given by $\vec r(t)=(x(t),y(t))$ for $a\leq t\leq b$. We know that the velocity is $\dfrac{d\vec r}{dt}$, and so the speed is just the magnitude of this vector.

Show that we can write the rover's speed at any time $t$ as $$\ds\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}.$$
If the rover moves at speed $\ds\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}$ for a little time length $dt$, what's the little distance $ds$ that the rover traveled?
Explain (Riemann sums may help) why the length of the path given by $\vec r(t)$ for $a\leq t\leq b$ is $$s=\int ds=\int_a^b \left|\frac{d\vec r}{dt}\right| dt=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt.$$
The path $\vec r(t) = (3\cos t, 3\sin t)$ for $0\leq t\leq 2\pi$ is a circle of radius 3. Verify that the formula above does in fact yield the circumference of this circle.
If the curve is in space (so $\vec r(t)=(x(t),y(t),z(t))$ is the path), then how does the arc length formula above change?
Are there any requirements we must know about the parametrization $\vec r$ so that the formula above is valid?

Task 4.3

Gravity is often the first example we encounter of a vector field. Other important vector fields arise when we study magnetism, electricity, fluid flow, and more. To analyze how a river flows, we can construct a plot of the river and at each point in the river we draw a vector that represents the velocity at that point. This creates a collection of many vectors drawn all at once, where the base of each velocity vector is placed at the point where the velocity occurs. For gravity, a similar picture can be drawn, though all the vectors will point down with the same magnitude. This task has us construct a plot of a vector field.

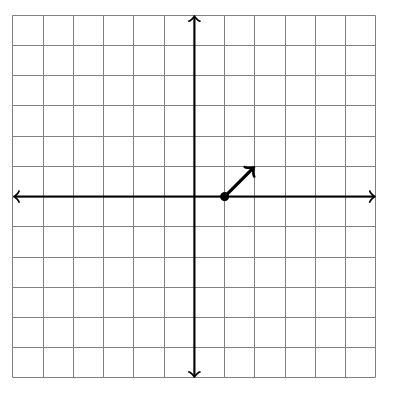
Consider the function $\vec F(x,y) = \left<x-2y,x+y\right>$. This is a function where the input is a point $(x,y)$ in the plane, and the output is the vector $\left<x-2y,x+y\right>$. For example, if we input the point $(1,0)$, then the output is $\left<1-2(0),1+0\right> = \left<1,1\right>$. To construct a vector field plot, we draw the vector $\left<1,1\right>$ with its base located at the input $(1,0)$. In the picture below, based at $(1,0)$ we draw a vector that points right 1 and up 1.

Complete the table below and add the other 7 vectors to the graph.
$\begin{array}{c|c} (x,y)&\left<x-2y,x+y\right>\\\hline (1,0)&\left<1,1\right>\\ (1,1)&\\ (1,-1)&\\ (0,1)&\\ (0,-1)&\\ (-1,0)&\\ (-1,1)&\\ (-1,-1)& \end{array}$
Repeat the above for the vector field $\vec F(x,y)=(-2y,3x)$, constructing a vector field plot consisting of 8 vectors.

Task 4.4

The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below.

section 3.2: checkpoint 3.7, exercises 75-92
Arc Length Practice: section 3.3: checkpoint 3.9, exercises 102-112

Day 4 - In class

Brain Gains (Rapid Recall, Jivin' Generation)

A rover follows the path given by $\vec r(t) = (3t,t^2)$. Find the velocity of the rover at $t=2$.
Give a vector equation of the tangent line to the rover's path at $t=2$, so $$\begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}?\\?\end{pmatrix} t+\begin{pmatrix}?\\?\end{pmatrix}.$$
Give the rover's speed at any time $t$.
An object travels along straight lines. Its velocity is $ (0,3,4) $ m/s for 2 seconds, and then turns so its velocity is $ (1,2,-2) $ m/s for 5 seconds. Show the total distance (arc length) traveled by the object is 25m. [Hint: find the speed from the velocity.]

Group Problems

Find the arc length of the curve $\vec r(t) = (t^2, t^3)$ for $0\leq t\leq 2$. Recall the arc length formula is $$\int_C ds = \int_a^b\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt.$$ Actually compute any integrals you encounter.
Draw the vector field $\vec F(x,y) = \langle2x+y,x+2y\rangle$. (Based at $(x,y)$, draw the vector $\langle2x+y,x+2y\rangle$.)
Draw the vector field $\vec F(x,y) = \langle y,-x\rangle$.
Draw $\vec r(t) = (3 \cos t, 3 \sin t)$.
- The curve above represents the position of an object. Compute the velocity of the object, so $\vec v(t) = \frac{d\vec r}{dt}$.
- State the speed of the object above (simplify your answer to get a speed of 3). What is the difference between velocity and speed?
Draw $\vec r(t) = (3 \cos 2t, 3 \sin 2t)$. (Suggestion - use multiples of $\pi/4$ for a table, rather than $\pi/2$. Why?) What is the speed of this curve? (Simplify the speed to get 6.)
Draw $\vec r(t) = (7 \cos 5t, 7 \sin 5t)$. What is the speed of this curve? (Did you get 35?)
Hurricane Matthew has a diameter of 28 miles. Assuming the eye is at the origin $(0,0)$, give a parametrization of the exterior edge of the hurricane.
- Sustained winds are 128 mi/hr. Modify your parametrization above so that the speed is 128 mi/hr.
- The eye of the hurricane is moving north west at a speed of 12 mi/hr. Modify your parametrization so that the center moves north west at 12 mi/hr.
Let $\vec F=(-10,0)$ N and $\vec d=(2,1)$ m. Recall the projection of $\vec F$ onto $\vec d$ is $\ds \text{proj}_\vec d\vec F = \frac{\vec F\cdot \vec d}{\vec d\cdot \vec d}\vec d$.
- Compute the projection of $\vec F$ onto $\vec d$ (so compute $\vec F_{\parallel \vec d}$).
- Draw $\vec F$, $\vec d$ and $\text{proj}_\vec d\vec F $ on the same grid, all with their base at the origin. Try your best to give the $x$ and $y$ directions the same scale, otherwise you won't be able to see the connections among vectors.
- Add to your picture the vector difference $\vec F_{\perp \vec d}=\vec F - \text{proj}_\vec d\vec F $. Which vectors in your picture are orthogonal?
- Draw $\text{proj}_\vec F\vec d $, without doing any computations. Have each group member do this, and discuss any differences.

Day 5 - Prep

Task 5.1

Work is a transfer of energy. When a force acts through a displacement, work is done. Gravity acts on falling objects, transferring potential energy to kinetic energy. Any force, when acting through a displacement, will result work done.

When a constant force and displacement are in the same straight line direction, the work done is simply the product of the magnitude of the force, and the distance.
When a constant force acts opposite a straight line displacement, the work is the negative of the magnitude of the force and the distance.

If a constant force is not parallel (or antiparallel) to a straight line displacement $\vec d$, then we instead use the component of the force that is parallel to the displacement (so $\vec F_{\parallel \vec d}$) to compute work.

Let $\vec F=(-1,2)$ and $\vec d=(3,4)$.

Start by computing $\vec F_{\parallel d} = \text{proj}_{\vec d}\vec F$ and $\vec F_{\perp d}$.
Construct a picture that shows the relationship between $\vec F,$ $\vec d$, $\text{proj}_{\vec d}\vec F$, and $\vec F_{\perp d}$.
Compute the work done by $\vec F$ through the displacement $\vec d$ by computing $|\vec F_{\parallel d}|$ and $|\vec d|$. Should the work be positive or negative?

Change the force to $\vec F = (-2,0)$. but keep $\vec d=(3,4)$.

Construct a similar picture as above, showing the relationship between $\vec F,$ $\vec d$, $\text{proj}_{\vec d}\vec F$, and $\vec F_{\perp d}$. Feel free to construct this picture with, or without, doing any computations.
Compute the work done by $\vec F$ through the displacment $\vec d$. Should the work be positive or negative?
Can you find a simpler way to compute the work done by $\vec F$ through $\vec d$ than computing $|\vec F_{\parallel d}|$ and $|\vec d|$?

Task 5.2

Find the length of the curve $\ds \vec r(t) = \left(t^3,\frac{3t^2}{2}\right)$ for $t\in[1,3]$. The notation $t\in[1,3]$ means $1\leq t\leq 3$. Be prepared to show us your integration steps in class (you'll need a substitution).
Now find the length of the helix $\vec r(t) = (2\cos t, 2\sin t, t)$ for $t\in [0, 4\pi] $.

Task 5.3

Suppose a rover is currently moving and has a velocity vector $\vec v = (3,4)$. A force acts on the rover causing an acceleration of $\vec a = (-1,5)$. The rover is currently at the location $(2,-3)$.

Draw picture that shows the rover's location along with the velocity and acceleration vectors drawn with their base at the rover's location.
Find the vector component of the acceleration that is parallel to the velocity (so find $\vec a_{\parallel \vec v}$), and then find the vector component of the acceleration that is orthogonal to the velocity (so find $\vec a_{\perp \vec v}$).
Will this acceleration cause the rover to speed up or slow down? Explain.
Will this acceleration cause the rover to turn left or right? Explain.

A probe above Mars is currently moving and has a velocity vector $\vec v = (-2,1,2)$. The onboard thrusters apply a force that causes an acceleration of $\vec a = (0,2,-3)$.

Find both $\vec a_{\parallel \vec v}$ and $\vec a_{\perp \vec v}$.
Will this acceleration cause the satellite to speed up or slow down? Explain.
How would you interpret $\vec a_{\perp \vec v}$?

Task 5.4