I-Learn, Class Pictures, Learning Targets, Text Book Practice
Prep Tasks: Unit 1 - Motion, Unit 2 - Derivatives, Unit 3 - Integration, Unit 4 - Vector Calculus

Day 3 - Prep

Task 3.1

Suppose for a short time that a rover follows a path given by $(x, y) = (1t + 3, −2t + 4)$. This is the same as writing $(x, y) = (1, −2)t + (3, 4)$.

Construct a plot that shows the location of the rover at time $t = 0, 1, 2$, and add some arrows as well as a line to illustrate the rover’s path.
What is the speed of the rover? (you may assume that distances are in meters, and time is in minutes).
What is the rover's velocity (hint, this should be a vector)?
When we write the path in the form $(x, y) = (1, −2)t + (3, 4)$, what do the quantities (1, −2) and (3, 4) have to do with the path?
The rover is no longer on flat ground, rather is sitting at point $P = (0, 2, 3)$. It starts to climb in the direction $\vec v = \langle 1, −1, 2\rangle$.
- Write a vector equation $(x, y, z) = (?, ?, ?)$ for the line that passes through the point $P$ and is parallel to $\vec v$.
- Generalize your work to give an equation of the line that passes through the point $P = (x_1 , y_1 , z_1)$ and is parallel to the vector $\vec v = (v_1 , v_2 , v_3 )$.

Task 3.2

Suppose the Curiosity rover travels in a circular path given by the parametric curve $\vec r(t) = (3 \cos t, 3 \sin t)$.

Graph the curve $\vec r$ (you should obtain a circle) and make sure you designate the direction in which the rover is traveling.
Compute both $\ds \frac{d \vec r}{dt}$ and $\ds\frac{d^2\vec r}{dt^2}$.
Locate the point on your graph that the rover is at when $t = \pi/2$. How would you describe the velocity and acceleration of the rover at this point? Compute both $\frac{d\vec r}{dt}(\frac{\pi}{2})$ and $\frac{d^2\vec r}{dt^2}(\frac{\pi}{2})$, and confirm that these vectors do indeed provide the acceleration and velocity of the rover at $t = \pi/2$.
Let's swap to the time $t = \pi/4$. On your graph, draw the vectors $\frac{d\vec r}{dt}(\frac{\pi}{4})$ and $\frac{d^2\vec r}{dt^2}(\frac{\pi}{4})$ with their tail placed on the curve at $\vec r(\frac{\pi}{4})$. These vectors are the velocity and acceleration.
Give a vector equation of the tangent line to this curve at $t = \pi/4$.

Task 3.3

Suppose a heavy box needs to be lowered down a ramp. The box exerts a downward force of say 200 Newtons (gravity), which we could write in vector notation as $\vec F=\left<0,-200\right>$. If the ramp was placed so that the box needed to be moved right 6 m, and down 3 m, then we'd need to get from the origin $(0,0)$ to the point $(6,-3)$. This displacement can be written as $\vec d=\left<6,-3\right>$. The force $\vec F$ acts straight down, rather than parallel to the displacement. Let's find out how much of the force $\vec F$ acts in the direction of the displacement. We are going to break the force $\vec F$ into two components, one component in the direction of $\vec d$, and another component orthogonal to $\vec d$. The component of the force that is parallel to $\vec d$ is useful in understanding energy computations. The component of the force that is orthogonal to $\vec d$ is useful in understanding surface friction.

We want to write $\vec F$ as the sum of two vectors $\vec F = \vec w+\vec n$, where $\vec w$ is parallel to $\vec d$ and $\vec n$ is orthogonal to $\vec d$. Since $\vec w$ is parallel to $\vec d$, we can write $\vec w=c\vec d$ for some unknown scalar $c$. This means that $\vec F=c\vec d+\vec n$.

Start by drawing a picture that shows how $\vec F$, $\vec d$, $\vec w$, and $\vec n$ are related.
Use the fact that $\vec n$ is orthogonal to $\vec d$ to show that $\ds c = \frac{\vec F\cdot \vec d}{\vec d\cdot \vec d}$. [Hint: Dot each side of $\vec F=c\vec d+\vec n$ with $\vec d$ and distribute. You'll need to use the fact that $\vec n$ and $\vec d$ are orthogonal to remove $\vec n\cdot \vec d$ from the problem.]
Now that we have a formula for $c$, use that formula to show that $\vec w = c\vec d = (80,-40)$. We call this the projection of $\vec F$ onto $\vec d$ (or the component of $\vec F$ that is parallel to $\vec d$), and write $$\text{proj}_{\vec d}\vec F = \vec F_{\parallel \vec d}= \left(\frac{\vec F\cdot \vec d}{\vec d\cdot \vec d}\right)\vec d.$$
Obtain a formula for $\vec n$, the component of the force that is orthogonal to $\vec d$. This is sometimes written as $\vec F_{\perp \vec d}$.

Task 3.4

The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below. Remember that you don't have to do all of the problems listed below, rather do a few from sections that you feel you need more practice with.

Equations of lines: Section 2.5, checkpoint 2.43 and exercises 243 - 250.
Derivatives of Vector Valued functions: Section 3.2, checkpoint 3.5 and exercises 41-54.
Projection practice: section 2.3, checkpoint 2.27 and exercises 167-172

Day 3 - In class

Brain Gains (Rapid Recall, Jivin' Generation)

1. For the curve $\vec r(t) = (t^2+2, -3t+4)$, note that $\frac{d\vec r}{dt} =(2t,-3)$. Give a vector equation of the tangent line to $\vec r(t)$ at $t=2$. In other words, give a vector equation of a line that passes through $\vec r(2) = (6,-2)$ and is parallel to $\frac{d\vec r}{dt}(2) = (4,-3)$.

Solution

Passing through $(6,-2)$ and parallel to $(4,-3)$ means an equation is $$(x,y) = (4,-3)t+(6,-2)\quad \text{or}\quad \vec r(t) = (4,-3)t+(6,-2).$$ This is the same as $$(x,y) = (4t+6,-3t-2).$$

2. The curve above represents the path of an object. Find the object's velocity and speed at any time $t$, and then at $t=1$.

Solution

The derivative $\frac{d\vec r}{dt} =(2t,-3)$ gives us the velocity at any time $t$. So at $t=1$ we have the velocity as $$\vec v = (2,-3).$$ The speed is the magnitude of the velocity, which gives the speed as $$v=|\vec v|=||\vec v|| = \sqrt{4t^2+9}.$$ At $t=1$ we have $v(1) = \sqrt{13}$. Note that we may use the same letter, without a vector symbol, to represent the magnitude of the corresponding vector, and you'll find that some people prefer double bars $||\vec v||$ instead of single bards $|\vec v|$.

3. The (vector) projection of $\vec P$ onto $\vec Q$ is given by the formula $$\ds \text{proj}_\vec Q\vec P = \frac{\vec P\cdot \vec Q}{\vec Q\cdot \vec Q}\vec Q.$$ Compute the projection of $\vec P$ onto $\vec Q$ using $P=(3,4)$ and $Q=(-2,5)$.

Solution

We compute $$\ds \text{proj}_\vec Q\vec P = \frac{\vec P\cdot \vec Q}{\vec Q\cdot \vec Q}\vec Q = \frac{(3)(-2)+(4)(5)}{(-2)^2+5^2}(-2,5) = \frac{14}{29}(-2,5) .$$ Note that this is a little less than half $\vec Q$.

Group Problems

Remember to pass the chalk after each problem (or part of a problem).

Give a vector equation of the line that passes through the point $(1,2,3)$ and $(-2,4,9)$.
An object starts at $P=(1,2,3)$ and each unit of time its displacement is $\vec v=(-4,5,1)$. Give an equation for the position $(x,y,z)$ at any time $t$.
- What is the speed of an object that follows the path described above?
Draw the parametric curve $\vec r(t) = (1+t^2,3t-2)$ for $-2\leq t\leq 3$.
- Give $\frac{d\vec r}{dt}$. Then state $\frac{dx}{dt}$, $\frac{dy}{dt}$, and $\frac{dy}{dx}$.
- Give a vector equation of the tangent line to the curve at $t=2$.
Let $P=(3,4)$ and $Q=(2,0)$.
- Using the formula $$\ds \text{proj}_\vec Q\vec P = \frac{\vec P\cdot \vec Q}{\vec Q\cdot \vec Q}\vec Q,$$ compute $\text{proj}_\vec Q\vec P$, the project of $\vec P$ onto $\vec Q$. We may also write this as $\vec P _{\parallel \vec Q}$, which we read as, "The vector component of $\vec P$ that is parallel to $\vec Q$."
- Draw $\vec P$, $\vec Q$ and $\text{proj}_\vec Q\vec P $ on the same grid with their base at the origin.
- Add to your picture the vector difference $\vec P_{\perp \vec Q} = \vec P - \text{proj}_{\vec Q}\vec P$, which we call "The vector component of $\vec P$ that is orthogonal to $\vec Q$." How is $\vec P_{\perp \vec Q}$ related to the other vectors?
- Now compute the projection of $\vec Q$ onto $\vec P$ (so swap which vector is projected onto the other).
- Draw $\vec P$, $\vec Q$ and $\text{proj}_\vec P\vec Q $ on the same grid with their base at the origin, and add to your picture the vector difference $\vec Q_{\perp \vec P} = \vec Q - \text{proj}_{\vec P}\vec Q $.
Repeat the previous problem with $P=(3,4)$ and $Q=(-1,1)$.

Day 4 - Prep

Task 4.1

Consider the curve $\vec r(t) = (2t+3, 4(2t-1)^2)$.

Construct a graph of $\vec r$ for $0\leq t\leq 2$.
If this curve represents the path of a rover (meters for distance, minutes for time), find the velocity of the rover at any time $t$, and then specifically at $t=1$. What is the rover's speed at $t=1$?
Give a vector equation of the tangent line to $\vec r$ at $t=1$. Include this on your graph.
State the rover's acceleration vector.
Explain how to obtain the slope of the tangent line, and then write an equation of the tangent line using point-slope form. [Hint: How can you turn the direction vector, which involves $(dx/dt)$ and $(dy/dt)$, into the number given by the slope $(dy/dx)$?]

Task 4.2

We are ready to tackle the problem of finding the length of a path. This length we call arc length. If a rover moves at a constant speed, then the distance traveled is simply $$\text{distance} = \text{speed}\times\text{time}.$$ This requires that the speed be constant. What if the speed is not constant? Over a really small time interval $dt$, the speed is almost constant, so we can still use the idea above.

Suppose a rover (or other object) moves along the path given by $\vec r(t)=(x(t),y(t))$ for $a\leq t\leq b$. We know that the velocity is $\dfrac{d\vec r}{dt}$, and so the speed is just the magnitude of this vector.

Show that we can write the rover's speed at any time $t$ as $$\ds\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}.$$
If the rover moves at speed $\ds\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}$ for a little time length $dt$, what's the little distance $ds$ that the rover traveled?
Explain (Riemann sums may help) why the length of the path given by $\vec r(t)$ for $a\leq t\leq b$ is $$s=\int ds=\int_a^b \left|\frac{d\vec r}{dt}\right| dt=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt.$$
The path $\vec r(t) = (3\cos t, 3\sin t)$ for $0\leq t\leq 2\pi$ is a circle of radius 3. Verify that the formula above does in fact yield the circumference of this circle.
If the curve is in space (so $\vec r(t)=(x(t),y(t),z(t))$ is the path), then how does the arc length formula above change?
Are there any requirements we must know about the parametrization $\vec r$ so that the formula above is valid?

Task 4.3

Gravity is often the first example we encounter of a vector field. Other important vector fields arise when we study magnetism, electricity, fluid flow, and more. To analyze how a river flows, we can construct a plot of the river and at each point in the river we draw a vector that represents the velocity at that point. This creates a collection of many vectors drawn all at once, where the base of each velocity vector is placed at the point where the velocity occurs. For gravity, a similar picture can be drawn, though all the vectors will point down with the same magnitude. This task has us construct a plot of a vector field.

Consider the function $\vec F(x,y) = \left<x-2y,x+y\right>$. This is a function where the input is a point $(x,y)$ in the plane, and the output is the vector $\left<x-2y,x+y\right>$. For example, if we input the point $(1,0)$, then the output is $\left<1-2(0),1+0\right> = \left<1,1\right>$. To construct a vector field plot, we draw the vector $\left<1,1\right>$ with its base located at the input $(1,0)$. In the picture below, based at $(1,0)$ we draw a vector that points right 1 and up 1.

Complete the table below and add the other 7 vectors to the graph.
$\begin{array}{c|c} (x,y)&\left<x-2y,x+y\right>\\\hline (1,0)&\left<1,1\right>\\ (1,1)&\\ (1,-1)&\\ (0,1)&\\ (0,-1)&\\ (-1,0)&\\ (-1,1)&\\ (-1,-1)& \end{array}$
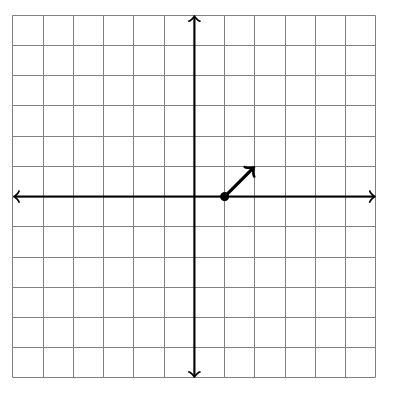
Repeat the above for the vector field $\vec F(x,y)=(-2y,3x)$, constructing a vector field plot consisting of 8 vectors.