Please Login to access more options.


Today

« September 2017 »

Sun

Mon

Tue

Wed

Thu

Fri

Sat

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

Once we have a set of permutations, we'd like to be able to combine them to get new permutations. The previous problem used repetition on simple shift permutations of the alphabet to obtain additional permutations. The next problem has you show that the composition of any finite collection of permutations on a set is always a permutation.

Theorem (The Composition Of Permutations Is A Permutation)

Let $X$ be a set. Suppose that $\sigma_1, \sigma_2, \ldots,\sigma_k$ are permutations of $X$. Then the composition $\sigma_1\circ \sigma_2\circ \ldots\circ \sigma_k$ is a permutation of $X$.

Problem 11 (The Composition Of Permutations Is A Permutation)

Prove theorem (The Composition Of Permutations Is A Permutation). As some reminders, you may use the following facts that you proved in either Math 301 or Math 340. You may use these facts without proof.

  • The composition of two injective functions is injective.
  • The composition of two surjective functions is surjective.
  • A function is a bijection if it is both injective (1 to 1) and surjective (onto). Hence, the composition of two bijective functions is a bijection.
  • You might find induction helps you get from a composition of two bijective functions is bijective to the composition of $n$ bijective functions is bijective.

Recall that given a set of vectors $S=\{\vec v_1, \vec v_2,\ldots, \vec v_k\}$, a linear combination of these vectors was a sum of the form $$c_1\vec v_1+c_2\vec v_2+\cdots+c_k\vec v_k.$$ The span of a set of vectors is the set of all linear combinations of the vectors. In linear algebra we took a small set of vectors and spanned the vectors to create vector spaces. We defined the span of $S$ to be the set of all linear combinations of vectors in $S$.

Given a permutation, we've shown that we can use function composition to create new permutations. If $S$ is a set of permutations on $X$, we'd like to have a way to talk about combining the permutations. Instead of multiplying by a scalar and adding, we'll decide how many times to repeatedly apply the function, and then compose different functions together.

Definition (Composition Combination Of Permutations)

Let $X$ be a set, and $S$ be a set of permutations of $X$.

  • If $\sigma$ is a permutation of $X$, we'll use exponential notation to express repeated composition of $\sigma$. This gives us $\sigma^2=\sigma\circ \sigma$ and $\sigma^5=\sigma\circ\sigma\circ\sigma\circ\sigma\circ\sigma$, etc.
  • We'll use negative exponents when we want to repeated apply an inverse, which gives us $\sigma^{-n}=\left(\sigma^{-1}\right)^n$.
  • A composition combination of permutations in $S$ is a composition of the form $$\sigma_1^{n_1}\circ\sigma_2^{n_2}\circ\cdots\circ \sigma_k^{n_k},$$ where $k\in\mathbb{N}$, each $\sigma_i\in S$, and each $n_i\in \mathbb{Z}$ for $i\in \{1,2,3,\ldots,k\}$.
  • The span of $S$, written $\text{span}(S)$ is the set of all composition combinations of permutations in $S$. We'll say that the set $S$ generates $\text{span}(S)$.

As an example, if $S=\{a,b,c,d\}$ is a set of permutations of $X$, then the composition $a^2\circ b^{-1}\circ c^3$ is a composition combination of permutations in $S$, and so are $d^{-3}$, $b^5\circ a^{-2}$, and more.

Problem 13 (Simple Shift Repetition Game)

Consider the set of simple shift permutations $H=\{\phi_n\mid n\in \mathbb{Z}\}$ on a 26 letter alphabet. We've shown that there are 26 different functions in this set. Consider the following game.

  • The first player picks an element $\sigma_1\in H$. They then remove from $H$ the span of $\sigma_1$ (so everything generated by $\{\sigma_1\}$).
  • The second player now chooses an element $\sigma_2\in H$ that hasn't yet been removed. They then remove from $H$ any element in the span of $\{\sigma_1,\sigma_2\}$. At this stage, any permutation that can be written as a composition combination of the permutations $\sigma_1$ and $\sigma_2$ has been removed.
  • Players alternate taking turns, choosing an element $\sigma_k\in H$ that hasn't been removed in a previous stage, and then removing from $H$ any element in the span of $\{\sigma_1,\sigma_2,\ldots,\sigma_k\}$.
  • Whoever take the last element of $H$ wins. The game can also be played as a misere game.

Answer the following questions.

  1. Player 1 takes $\phi_6$. Which elements should be removed from $H$
  2. Is there a way for player 1 to win on the first move? Explain.
  3. What's the largest number of turns that can occur in this game (so if neither player tries to win, how long can the game go on)?
  4. If we play this as a misere game, does player 1 have a winning strategy?

Problem 14(The Span Of A Simple Shift)

Suppose that our alphabet $S$ consists of only 12 letters $S=\{a,b,c,d,e,f,g,h,i,j,k,l\}$. Let $H_{12}=\{\phi_n\mid n\in \mathbb{Z}\}$ be the set of simple shift permutations on this 12 letter alphabet (we wrap around from $l$ to $a$).

  1. For each $n\in \{0,1,2,\ldots,11\}$, list the elements in $\text{span}(\{\phi_n\} ) $.
  2. For which $n$ does $\text{span}(\{\phi_n\})=H_{12}$.
  3. Make a conjecture about any patterns you see above and their relation to the size (12) of the alphabet.
  4. Whenever you make a conjecture, you should always test your conjecture on an example you have not yet considered. Pick another integer $k\neq 12,26$, and look at the set $H_k$ of simple shift permutations of an alphabet consisting of $k$ letters. Then check if your conjecture holds.

Much of our work up to this point has been based on the ability to compute a remainder. This is all based on the Division Algorithm.

Theorem (Division Algorithm)

Let $a,n\in\mathbb{Z}$, with $n> 0$. Then there exists unique integers $q$ and $r$ (called the quotient and remainder) such that $a=qn+r$ where $0\leq r<n$.

Problem 15(Division Algorithm Proof)

Prove the Division algorithm.

If you are unable to complete the previous problem, it's OK to move on to the next. You may find that reading chapter 0 in your abstract algebra text can help you with this one.

One of our main uses of the division algorithm is modular arithmetic.

Definition (Modular Arithmetic)

Let $a,b,n\in \mathbb{Z}$ with $n>0$. We say that two integers $a$ and $b$ are congruent mod $n$, and write $a \mod n= b\mod n$, if they have the same remainder after dividing by $n$. If $a=qn+r$ where $r$ is the remainder after dividing by $n$, then we'll often write $r=a\mod n$. There are lots of ways to denote this in the literature. We might say $r\equiv a\mod n$, $r=a\pmod n$, $a\mod n \equiv b \mod n$, and more.

Problem 16(Remainders Equal Iff Difference Is A Multiple)

Let $a,b,n\in\mathbb{Z}$ with $n>0$. Prove that $a\pmod n = b \pmod n$ if and only if $a-b$ is a multiple of $n$.

Many encryption algorithms depend entirely on modular arithmetic. The RSA public key encryption algorithm requires that we compute extremely large powers of rather large numbers. For example, we might need to compute $2348971^{986871578457358918334698187}$. This can be an expensive operation, unless we find some patterns to help us. The next problem provides a beginning at doing this.

Problem 17(Computing Powers Modn Conjecture)

We need to be able to compute $a^k\pmod n$.

  1. Compute $2^k\pmod 5$ for $k=1,2,3,4,5,6,7$. What pattern do you see. What is $2^k\pmod 5 $ for $k=257$ and for $k=49827512$.
  2. Compute $5^k\pmod {11}$ for $k=1,2,3,4,5,6,7,8,9,10,11,12$. Can you discover a pattern. What if $k=3047$ or $k=478209183234$?
  3. Make a conjecture about $a^k\pmod n$. Come up with a different example to back your conjecture.

We need a common notation to talk about permutations. If $\sigma$ is a permutation of $X=\{1,2,3,4,5,6\}$, then we could use the matrix notation $ \sigma= \begin{bmatrix}1&2&3&4&5&6\\2&4&6&1&5&3\end{bmatrix} $ to represent the permutation $$ \sigma(1)=2,\sigma(2)=4,\sigma(3)=6,\sigma(4)=1,\sigma(5)=5,\sigma(6)=3 $$ Alternately, we could look at cycling patterns that occur in the permutation and write $1\to 2\to 4\to 1$ and then stop because at this point the cycle repeats. We'd also need to write $3\to 6\to 3$ and $5\to 5$, though if we left the $5\to 5$ part off we could assume that 5 did not change. Rather than writing the arrows, we'll represent this permutation by writing $\sigma=(1,2,4)(3,6)(5)$, or leaving off the fact that 5 maps to itself we could just write $\sigma=(1,2,4)(3,6)$. We can use this notation to express any permutation. We need a formal definition for this cycle notation. You can read more about disjoint cycle notation on page 98 in Gallian's Contemporary Abstract Algebra.

Definition (Disjoint Cycle Notation)

Let $X=\{1,2,3,\ldots ,n\}$ for some positive integer $n$. Let $\sigma$ be a permutation which we have written in the matrix form $ \sigma= \begin{bmatrix}1&2&\cdots&n\\\sigma(1)&\sigma(2)&\cdots&\sigma(n)\end{bmatrix}. $ Let $a_1\in X$ (often we choose $a_1=1)$ and then compute $\sigma(a_1),\sigma^2(a_1),\sigma^3(a_n),\ldots, \sigma^{k_1}(a_n)$ until the next application of $\sigma$ returns $a_1$. This gives the first cycle (vector) $\alpha_1=(a_1,\sigma(a_1),\ldots,\sigma^{k_1}(a_1))$. We then pick $a_2\in X$ so that $a_2$ is not an entry in $\alpha_1$, and repeat this process to obtain a second cycle $\alpha_2=(a_2,\sigma(a_2),\sigma^2(a_2),\ldots,\sigma^{k_2}(a_2))$. We then pick $a_3\in X$ so that $a_3$ is not an entry in $\alpha_1$ nor $\alpha_2$, and repeat the process to obtain the cycle $\alpha_3$. At each stage we pick a new element $a_k\in X$ that is not an entry in any of $\alpha_1,\alpha_2,\ldots, \alpha_{k-1}$, and then repeatedly apply $\sigma$ to obtain the cycle $a_k$. The process stops when every element of $X$ is in $\alpha_k$ for some $k$. We then write $$\sigma=\alpha_1\circ\alpha_2\circ\cdots \circ \alpha_m = \alpha_1\alpha_2\cdots\alpha_m$$ where $m$ is the number of cycles needed to represent the permutation. Whether we include the composition symbol or not is a matter of preference.

We will often omit writing singleton vectors $(a)$. So if $X=\{1,2,3,4\}$, then instead of writing $(1)(2,3)(4)$, we'll just write $(2,3)$. The permutation $(2,3)$ does not change the elements $1$ and $4$, so we omit writing them. The identity permutation would be $(1)(2)(3)(4)$. We could omit all singletons which would leave us with nothing, so in this case we'll write $()$ to represent the identity permutation.

Problem 18(Disjoint Cycle Notation Practice With Automorphisms Of A Square)

We have already shown that there are 8 automorphisms of the graph below.

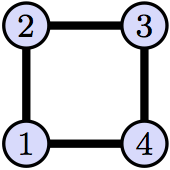
Write each of these automorphism using disjoint cycle notation. As an example, the automorphism that leaves 1 and 3 unchanged, but swaps 2 and 4, we write as $(1)(2,4)(3)$.

Problem 19(Automorphisms On Several Graphs With 4 Vertices)

Consider the two graphs below.

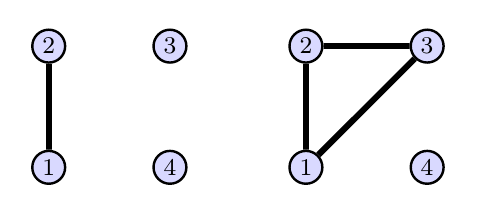
  1. For each graph, list the automorphisms of the graph. Use disjoint cycle notation to represent each automorphism.
  2. For each automorphism, state the smallest positive value of $k$ for which $\sigma^k$ is the identity automorphism. This is called the order of the automorphism.
  3. Construct another graph on 4 vertices different than the three we have seen so far. How many automorphisms does this graph have? Explain.

For more problems, see AllProblems