Math 441 - Abstract Algebra - Schedule

Please Login to access more options.

Since elementary school, you've been doing division. The following theorem is a crucial beginning place for much of our work in abstract algebra. It gives a formal meaning to the quotient and remainder when performing division.

Theorem (Division Algorithm)

Let $a,n\in\mathbb{Z}$, with $n> 0$. Then there exists unique integers $q$ and $r$ (called the quotient and remainder) such that $a=qn+r$ where $0\leq r<n$.

Anytime you see a new word, a new theorem, a new problem, etc., making an example to illustrate the new idea is crucial, as well as being able to recognize when something closely related is not an example. As the semester progresses, we'll be doing this with each new problem we work on. Sometimes the problem itself will ask you to create the example, and sometimes you'll just need to make it yourself. Here's an example of how to give an example and non example of the theorem given above.

Example

If we let $a=23$ and $n=5$, then we can write $23=4\cdot 5+3$. The quotient is $q=4$ and the remainder is $r=3$. Notice that $0\leq r<5$.

Non Example

Let $a=-23$ and $n=5$. We can write $-23=(-4)\cdot 5-3$, so it might be tempting to say that the quotient is $q=-4$ and the remainder is $r=-3$. However notice that it is not true that $0\leq r<5$. The remainder cannot be negative, and must be less than $n$. Instead we can write $-23=(-5)\cdot 5+2$. This means the quotient is $q=-5$ and the remainder is $r=2$.

We'll come back to the division algorithm very soon, and give a formal proof. You are welcome to start working on the proof now for homework. You'll see the division algorithm show up in several places as you work the first few weeks of problems.

Problem 1 (The Game Of Scoring)

The game of Scoring is a two-player game. Start by creating a pile of $n\geq 1$ objects (feel free to choose $n$ however you want). On each player's turn, they must choose 1, 2, or 3 items from the pile. Players alternate taking turns until someone takes the last object. Whoever takes the last object wins.

Play this game several times with various values of $n$.
For which values of $n$ does the first player have a winning strategy (meaning they are guaranteed to win if they play correctly). Remember to always fully justify your answers.
For which values of $n$ does the second player have a winning strategy? Why?
For which values of $n$ does the first player have a winning strategy if we change the rules so that now each player must choose 1, 2, 3, or 4 items from the pile.
We'll now change the rules and require a player to take anywhere from 1 to $k$ objects each turn. Conjecture the values of $n$ for which the first player has a winning strategy.

Problem 2 (The Game Of Scoring Misere)

A misere game is a game played by the regular rules with one change; whoever wins the game according the regular rules is the loser. Consider again the game of Scoring, but this time we'll play it as a misere game.

For which values of $n$ does the first player have a winning strategy when playing misere, provided each player must take 1, 2, or 3 objects?
For which values of $n$ does the first player have a winning strategy when playing misere, provided each player must take 1, 2, 3, or 4 objects?
If instead a player must take between 1 and $k$ objects, conjecture the values of $n$ for which the first player has a winning strategy when playing misere.

Definition (Encryption Key)

An encryption key is an algorithm which specifies how a message is to be encoded. The encrypted message is often called ciphertext. The original message is called plain text. See Wikipedia for more information.

Definition (Simple Shift Permutation Of The Alphabet)

Let $M$ be a message, which we will think of as a sequence of letters from the standard 26 letter Roman alphabet. We can write $M=(m_1,m_2,m_3, \ldots, m_n)$ where $m_i\in\{a, b, c, \ldots, z\}$. For simplicity, our messages are not case-sensitive and all spaces and punctuation have been removed. To send the phrase "Let's meet at dawn." we'd just use the plain text message $M=(l,e,t,s,m,e,e,t,a,t,d,a,w,n)$.

We now define an encryption key to produce ciphertext from a message $M$. Given a message $M=(m_1,m_2,m_3, \ldots, m_n)$, let $\phi_3(m_i)$ be the letter in the alphabet that has been shifted three right from the current letter. When we hit the end of the alphabet, we'll wrap around so that shifting $z$ right one gets us to $a$. Let's call this the simple shift permutation $\phi_3$. So we now have $\phi_3(a)=d$, $\phi_3(m)=p$, and $\phi_3(z)=c$. In a similar manner, we can define the simple shift permutation $\phi_n$ which shifts each letter right $n$ units.

Problem 3 (First Encryption Key)

Suppose you encounter some ciphertext $(i,q,x,x,p,a,z,q)$ that you know has been encrypted using a simple shift permutation $\phi_n$ for some $n$.

Decode the ciphertext and state the original message. State the value of $n$ that was used to encode the original message.
Encode the plain text message "attack at dawn" into ciphertext using the same encryption key you discovered in the first part.
Are there any other $n$ that would have produced the same results as above? Be ready to fully justify your answer.

Problem 4 (The Set Of Simple Shift Permutations)

Let $S = \{a,b,c,\ldots,z\}$ be the set of letters in the Roman alphabet. For each $n\in\mathbb{Z}$, let $\phi_{n}:S\to S$ represent the encryption key that shifts each letter in the alphabet right $n$, where we wrap around from $z$ to $a$ for letters that need to be shifted past $z$. So $\phi_3(a)=d$, $\phi_3(b)=e$, and $\phi_3(z)=c$. We've called this a simple shift permutation of $S$.

For which $n$ does $\phi_n$ not change the message?
Consider the encryption key $\phi_{9}$, which shifts each letter right 9. If a message had been encrypted using $\phi_9$, then clearly $\phi_{-9}$ would decrypt the message as $\phi_{-9}(\phi_9(s))=s$ for any letter $s$. Give a positive integer $n$ that we could also use to decode a message that has been encrypted using $\phi_9$.
Does $\phi_{30}=\phi_7$? Does $\phi_{33}=\phi_7$? For which $n$ does $\phi_n=\phi_7$? Explain.
Consider the set of all shifts of $S$, namely $H=\{\phi_n\mid n\in\mathbb{Z}\}$. How many different functions are in $H$? Prove your answer is correct.

Definition (Permutation)

Let $X$ be a set. A $\textdef{permutation}$ of $X$ is a bijection from $X$ to $X$, so it's a function from $X$ into $X$ that is both one-to-one and onto. We can think of a permutation of $X$ as a way of rearranging the elements in $X$. The identity permutation is the permutation $id_X:X\to X$ defined by $id_X(x)=x$.

Problem 5 (Number Of Permutations)

Given finite set $X$ with $n$ elements, how many permutations are there of $X$?

Show that if $X=\{1\}$, then there is only one permutation of $X$.
Show that if $X=\{1,2\}$, then there are two permutations of $X$. List them.
Make a list of all permutations of $X=\{1,2,3\}$, and then of $X=\{1,2,3,4\}$. What pattern do you see?
Make a conjecture about the number of permutation of $X$ if $|X|=n$. Then prove your conjecture.

Definition (Automorphism Of A Graph)

An $\textdef{automorphism of a graph}$ is a permutation $\sigma$ of the set of vertices such that two vertices $x$ and $y$ form an edge if and only if $\sigma(x)$ and $\sigma(y)$ form an edge. The $\textdef{automorphism group of a graph}$ is the set of all automorphisms of the graph. If $\mathcal{G}$ is a graph, its automorphism group is denoted $\aut(\mathcal{G})$.

Problem 6 (Automorphisms Of A Square)

Consider the graph $\mathcal{G} = (V,E)$ drawn below. The vertex set is $V = \{1,2,3,4\}$ and the set of edges is $$E = \{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}.$$

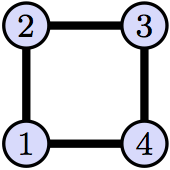
Write down all the automorphisms of $\mathcal{G}$ (there are more than 4, but less than 10). Explain how you know you have listed every automorhpism of $\mathcal{G}$.

This problem continues in AutomorphismsOfASquare2.

For more problems, see AllProblems

20170911