20160928

Please Login to access more options.

Today

Definition (The Order Of A Permutation)

The order of a permutation $\sigma$ is the smallest positive integer $n$ such that $\sigma^n$ equals the identity permutation.

Definition (The Game of Permutation Scoring also called Generate/Don't Generate)

Just as in the Simple Shift Repetition Game, we can play a similar game with any set of permutations of the same set $X$. Let $H$ be a set of permutations of a set $X$. We'll generally assume that the set $X$ is finite so that the game is guaranteed to end. However, you can play this game with an infinite set $X$.

Here are the rules.

• The first player picks an element $\sigma_1\in H$. They then remove from $H$ the span of $\{\sigma_1\}$ (so everything generated by $\sigma_1$).
• The second player now chooses an element $\sigma_2\in H$ that hasn't yet been removed. They then remove from $H$ any element in the span of $\{\sigma_1,\sigma_2\}$. At this stage, any permutation that can be written as a composition combination of the permutations $\sigma_1$ and $\sigma_2$ has been removed.
• Players alternate taking turns, choosing an element $\sigma_k\in H$ that hasn't been removed in a previous stage, and then removing from $H$ any element in the span of $\{\sigma_1,\sigma_2,\ldots,\sigma_k\}$.
• Whoever takes the last element of $H$ wins.

There are several variations:

• The game can also be played as a misere game, where whoever takes the last element of $H$ wins.
• You win by taking the last element. However, you cannot take the last element unless there are no other legal choices. So you can't try to win, rather you must be forced to win.

Problem 20(The Game Of Permutation Scoring On A Square)

Let's play the game of scoring on the automorphism group of the square. We know there are 8 automorphism. Play this game a few times to get a feel for what different choices will give.

1. Show there is no way for player 1 to win on the first move.
2. If player 1 takes any of the flips for their first move, what should player 2 choose to win the game?
3. Does player 1 have a winning strategy? What is it?

It would be nice if we could create a way to visually keeping track of which elements of $H$ have been taken. Let me describe how we can do this with an example. Suppose you are playing the game on a square (as above). Player one takes the permutation $(1,2,3,4)$. Then player $2$ chooses the element $(1,2)(3,4)$. Here's how we make the graph.

• Each element in $H$ will represent a vertex.
• When player 1 chooses $(1,2,3,4)$, pick a color (I'll choose red) and then draw a red arrow from each permutation $\sigma\in H$ to the permutation $(1,2,3,4)\circ \sigma$. In other words, we're going to draw a graph that shows what happens if we apply the automorphism $(1,2,3,4)$ after doing any other automorphism. If we start at the identity permutation $()=(1)(2)(3)(4)$, then we have $(1,2,3,4)\circ ()=(1,2,3,4)$, so we draw a red arrow from $()$ to $(1,2,3,4)$. Similarly, starting at $(1,2,3,4)$ we draw an arrow to $(1,2,3,4)\circ(1,2,3,4)=(1,3)(2,4)$. Continuing in this fashion for each permutation gives us the graph below, with two red cycles of 4.

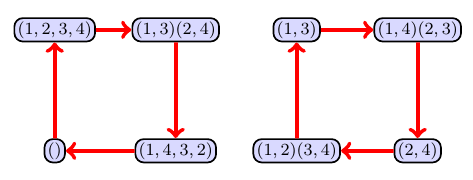
• The elements that are removed after choosing $(1,2,3,4)$ are any elements that we can get to by following a path that contains $(1,2,3,4)$. These are the 4 automorphisms in the cycle on the left.
• Now player 2 chooses $(1,2)(3,4)$. We now use a different color (I chose blue in the example below), and then at each vertex draw an arrow starting at $\sigma\in H$ and ending at $(1,2)(3,4)\circ \sigma$. The tricky part is finding a nice way to draw the graph without to many edge crossings (do you see how the outer circle flipped directions). Both of the examples below are ways to represent this graph. We can use an edge with an arrow on each end to illustrate that there is an arrow going both ways.

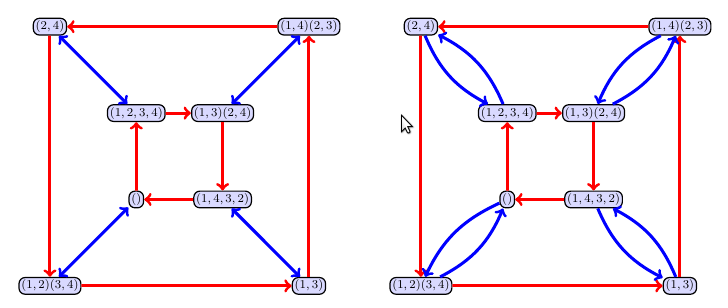
• The arrows in the graph above represent composition by either $(1,2,3,4)$ or $(1,2)(3,4)$. If you start at $(1,3)$ and want to compute $(1,2,3,4)\circ(1,2)(3,4)\circ(1,3)$, then you just have to start at $(1,3)$, follow the blue arrow to get to $(1,2)(3,4)\circ(1,3)=(1,4,3,2)$, and then follow the red arrow to get to $(1,2,3,4)\circ(1,4,3,2)$.

The mathematical program Sage can also help with the computations. The command PermutationGroup() below creates the span of the permutations listed. The command cayley_graph() creates the graph described above, but only shows the part of the graph that contains the permutations listed. Try executing the block of code below.

g1 = PermutationGroup(["(1,2,3,4)"])   #The set g1 is the span of the permutations listed.
d1=g1.cayley_graph()                   #This creates the Cayley graph of the g1. 
d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) #This shows the Cayley graph. 
print(g1.list())                       #This print a list of the elements in g1. 

g2 = PermutationGroup(["(1,2,3,4)", "(1,2)(3,4)"])
d2=g2.cayley_graph()
d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True)
print(g2.list())

Problem 21 (Composing Permutations Using Disjoint Cycle Notation)

Let $R_{90}=(1,2,3,4)$ and $H=(1,2)(3,4)$.

1. Express the compositions $R_{90}\circ H$ and $H\circ R_{90}$ in cycle notation. Be prepared to explain how you computed this.
2. Express the compositions $R_{90}\circ (1,3)$ and $H\circ (1,3)$ in cycle notation. Can you see these products in the graph above?
3. Express the composition $(1,2,4)\circ (1,4)(2,3)\circ (2,4)$ in cycle notation. Note that $(1,2,4)$ is not an automorphism of the square, but is a permutation.
4. Evalute the Sage command below. In the second graph below you should see that starting at $()$ and following the colored arrows corresponding to $(2,4)$ and then $(1,4)(2,3)$ gets you to the element $(1,4,3,2)$ which is precisely the composition $(1,4)(2,3)\circ (2,4)$. In the third graph below, if you start at the identity $()$ and the follow the colored arrow corresponding to $ (2,4)$, and then $(1,4)(2,3)$, and then $(1,2,4)$, you should end up at the same spot as you did in part 3. Click evaluate again if the graph you have is hard to read (as the graph will redraw).

g1 =  PermutationGroup(["(2,4)"])      #The set g1 is the span of the permutations listed.
d1=g1.cayley_graph()                   #This creates the Cayley graph of the g1. 
d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True) #This shows the Cayley graph. 
print(g1.list())                       #This print a list of the elements in g1. 

g2 = PermutationGroup(["(2,4)","(1,4)(2,3)"]) 
d2=g2.cayley_graph()
d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True)
print(g2.list())

g3 = PermutationGroup(["(2,4)","(1,4)(2,3)", "(1,2,4)"]) 
d3=g3.cayley_graph()
d3.show(color_by_label=True, vertex_size=0.03, vertex_labels=True,figsize=8)
print(g3.list())

Problem 22 (Creating Cayley Graphs Of Simple Shift Permutations)

Let's make some Cayley graphs as they relate with the game of Scoring on simple shift permutations. To get Sage to make the graphs, you'll first have to write the simple shift permutation in disjoint cycle notation. As an example, if there are 6 letters in our alphabet $X=\{1,2,3,4,5,6\}$, then we could write the simple shift $\phi_2$ as $(2,4,6)(1,3,5)$. If player 1 chooses $\sigma_1=\phi_2$ and player 2 chooses $\sigma_2=\phi_3$, then the following Sage code visually provides a graph of $\text{span}(\{\sigma_1\})$ and then $\text{span}(\{\sigma_1,\sigma_2\})$.

g1 =  PermutationGroup(["(2,4,6)(1,3,5)"])    
d1=g1.cayley_graph()                                                 
d1.show(color_by_label=True, vertex_size=0.03, vertex_labels=True)   
print(g1.list())                                                     

g2 = PermutationGroup(["(2,4,6)(1,3,5)","(1,4)(2,5)(3,6)"]) 
d2=g2.cayley_graph()
d2.show(color_by_label=True, vertex_size=0.03, vertex_labels=True)
print(g2.list())

By hand, my first graph would contain two unconnected triangles. My second graph would look similar to the graph above.

1. Suppose the alphabet is $X=\{1,2,3,4,5,6\}$. Player 1 chooses $\phi_1$. Draw the associated graph.
2. Suppose the alphabet is $X=\{1,2,\ldots,10\}$. Player 1 chooses $\phi_5$. Player 2 chooses $\phi_4$. Draw the two associated graphs.
3. Suppose the alphabet is $X=\{1,2,\ldots,12\}$. Player 1 chooses $\phi_5$. Draw the associated graph.
4. Suppose the alphabet is $X=\{1,2,\ldots,12\}$. Player 1 chooses $\phi_6$. Player 2 chooses $\phi_2$. Player 1 then chooses $\phi_3$. Draw the three associated graphs. The first graph should consist of 6 arrows between pairs of vertices (Sage will only show you the segment connnecting $()$ and $\phi_6$). Your second graph should have 2 hexagons with arrows crossing in the middle. The last graph should connect the edges of the hexagons.

Here's a blank Sage cell that you can use to perform some computations. You'll probably want to copy code from above and make some changes.

When we create graphs with Sage, it always creates a graph of the span of the permutations given. These graphs have a lot of really nice symmetry properties, and these properties are central to abstract algebra.

Problem 23 (Permutation Scoring On S 3)

Consider the game of permutation scoring on the set $S_3$, where $S_3$ represents the set of all permutations of $X=\{1,2,3\}$. We already know that there are 6 elements in $S_3$.

1. Play the game of permutation scoring on $S_3$. Play it a few times.
2. Can player 1 win by choosing a single permutation in $S_3$?
3. Does player $1$ have a winning strategy? What is it?
4. Pick an element in $S_3$ other than the identity, and call it $\sigma$. Let $S=\text{span}(\sigma)$. What is the span of $S$?
5. Repeat part 4 with a different element of $S_3$. You can use Sage to make this part fast (first compute the span of $\sigma$ with Sage. The list below the graph gives you the elements of the span. Then create a graph using these elements.
6. Make a conjecture.

Definition (A Closed Set Of Permutations)

We say that a set of permutations is closed if the set $S$ is equal to its span, so notionally we write $$S=\text{span}{(S)}.$$ In other words, we say that $S$ is closed if the set $S$ already contains every composition combination of permutations of elements in $S$.

Problem 24 (The Span Of A Set Of Permutations Is Closed)

Let $S$ be a set of permutations of $X$. Show that $\text{span}(S)$ is closed. In other words, show that once you form the span of a set $S$ of permutations of $X$, you cannot obtain any new permutations by spanning the span. For this reason, we'll often refer to $\text{span}(S)$ as the closure of $S$.

We'll be using modular arithmetic in a lot of things that we do throughout the semester. Let's invent a notation to help us talk about modular arithmetic.

Definition (The Set ZN Of Integers Mod N)

For each positive integer $n$, let $\mathbb{Z}_n=\{0,1,2,\ldots, n-1\}$ which is the same as $\mathbb{Z}_n = \{k\mod n\mid k\in \mathbb{Z}\}$. This is just the set of remainders when dividing by $n$. We'll refer to them as the integers modulo $n$, or the integers mod $n$.

Question

Take a look at the last question of The Set Of Simple Shift Permutations. Does this definition look familiar?

In previous problems, we've been using without proof some facts about modular arithmetic, namely that we can perform addition and subtraction either before or after we compute a remainder. Let's prove this is true.

Problem 25 (Modular Arithmetic Properties)

Let $n$ be a positive integer. Let $a,b\in \mathbb{Z}$.

1. Show that $((a \mod n)+(b\mod n))\mod n = (a+b)\mod n$. In other words, show that the sum of the remainders has the same remainder as the original sum.
2. Show that $((a \mod n)(b\mod n))\mod n = (ab)\mod n$. In other words, show that the product of the remainders has the same remainder as the original product.

Remember, you'll want to use the division algorithm to obtain quotient and remainders when dividing $a$, $b$, $ab$, and $a+b$ by $n$. You'll need to use the problem, Remainders Equal Iff Difference Is A Multiple, to complete your work.

Problem 26 (Powers With Modular Arithmetic)

1. We know that $481\mod {483} =(-2)\mod {483}$. Use this fact to quickly compute $481^2\mod{483}$ without a calculator. [How can you use the $-2$ to simplify this?]
2. Using the same idea, what is $481^{3}\mod{483}$ and $481^4\mod{483}$? You should be giving a positive integer less than 483 for all your answers.
3. Explain why $12\cdot 16 \mod 17$ is the same as $(-5)(-1)\mod 17$.
4. Now compute $14^k \pmod {17}$ without a calculator for as many values of $k$ as needed until you find a repeating pattern. See the hint below.

Let me give you a suggestion. Rather than trying to compute $14^4$, instead first compute $14^2$ by considering $(-3)^2$. To compute $(14)^3$, instead use the product $(14)^2(14)=(9)(-3)=(-8)(-3)$. Use your work from the previous power to figure out the next power. If you try to do this with brute force, it gets outrageously large really fast. If you swap from positive to negative values when the numbers get large (above 8), you should be able to do this without ever needing long division. You should find that no product ever gets above 24.

The following Sage code will compute powers with modular arithmetic. You are welcome to check your answers with this, but the whole point to the problem is to learn how to simplify the computations by hand. To compute $a^m\mod n$ you would write "power_mod($a$,$m$,$n$)."

power_mod(481, 4, 483)

Problem 27 (Matrix Encryption Mod 5)

In the Problem (Simple Matrix Encryption), we took a plain text message written in columns of a matrix $M$ and a matrix $A$ and used the product $AM$ to encode a message. Let's now combine matrix encryption with modular arithmetic to obtain a new encryption scheme. Once we have done this, we'll be one step closer to understanding modern encryption techniques. To simplify our work, let's use a small alphabet consisting of 5 letters. Instead of using the set $S=\{a,b,c,d,e\}$, let's just use numbers for our letters and we'll consider the alphabet $S=\{0,1,2,3,4\}=\mathbb{Z}_5$. Given the plain text "bad bed" or "10 31 43", we can encode it in the columns of the matrix $$M=\begin{bmatrix}1&3&4\\0&1&3\end{bmatrix}.$$ An 2 by 2 encryption key using coefficients mod 5 is a 2 by 2 matrix $A=\begin{bmatrix}a&b\\c&d\end{bmatrix}$ where $a,b,c,d\in \mathbb{Z}_5$. Here are the steps to our encryption scheme.

• First convert the plain text to a matrix $M$ where the letters are place in the matrix top to bottom, column by column.
• Take the encryption key $A$ and compute the product $AM$.
• Reduce all the entries in $AM$ mod 5. So the cipher text only consists of the numbers in $\mathbb{Z}_5$.

Answer the following questions.

1. Suppose we let $A=\begin{bmatrix}4&2\\1&3\end{bmatrix}$. Why is this matrix not suitable as an encryption key? (Hint: what is the determinant, and why is that a problem?)
2. Suppose we let $A=\begin{bmatrix}2&1\\4&3\end{bmatrix}$. The inverse of $A$ if we ignore modular arithmetic is $\frac{1}{2}\begin{bmatrix}3&-1\\-4&2\end{bmatrix}$. We know that we can replace $-4$ with $1$ when working modular 5. Similarly we can replace $-1$ with a positive number. We need to find the multiplicative inverse of 2 when working modular 5. Find a value $b\in \mathbb{Z}_5$ so that $2b\mod 5=1$. This number $b$ is the inverse of $2$ modular 5.
3. State a matrix $B$ with coefficients in $\mathbb{Z}_5$ so that $AB$ is the identity matrix after reducing each entry mod 5. Actually perform the product by hand, and show how this matrix product reduces to the identity.

Definition (Modular Multiplicative Inverse and $U(n)$)

Let $n$ be a positive integer, and let $a\in \mathbb{Z}_n$. Then the modular multiplicative inverse of $a \mod n$ is an integer $b\in \mathbb{Z}_n$ such that $(ab)\mod n=1$. If such an integer exists, then we'll write $a^{-1}\mod n$ to represent the modular multiplicative inverse. If the context is clear, we may just refer to this as the inverse instead of the modular multiplicative inverse. We'll use the notation $U(n)$ to represent the set of elements in $\mathbb{Z}$ that have a modular multiplicative inverse. Notationaly, we write $$U(n)=\{a\in\mathbb{Z}_n\mid \text{ there exists } b\in \mathbb{Z}_n \text{ such that } (ab)\mod n=1\}.$$

The Sage code "inverse_mod(a,n)" will compute the modular multiplicative inverse of $a\mod n$ or return an error.

inverse_mod(7, 11)

Problem 28 (Computing Multiplicative Inverses For Small N)

To use modular arithmetic in matrix encryption, we must be able to find the modular multiplicative inverse of $a \mod n$. For each $n\leq 13$ and $a\in \mathbb{Z}_n$, we now compute the inverse of $a\mod n$ or explain why it does not have one.

1. Why does $0\mod n$ never have an inverse?
2. What is the multiplicative inverse of $1\mod n$?
3. For $n=3$, what is the multiplicative inverse of $a=2$.
4. For $n=4$, show that 2 does not have an inverse by computing $2\cdot 0$, $2\cdot 1$, $2\cdot 2$, and $2\cdot 3$ all modulo $4$. What is $3^{-1}\mod 4$?
5. For each $n$ between 5 and 13, create a table that shows the inverse of each $a\in \mathbb{Z}_n$. List the elements of $\mathbb{Z}_n$ along the top row, and beneath each element list the multiplicative inverse, or cross off the number if there is no multiplicative inverse.

When you are done you should have a list of the elements of $U(n)$ for each $n$ up to 13, as well as the inverse of each element in $U(n)$. Do you see any patterns?

For $n=9$, you should obtain a table somewhat similar to the following table.

Definition (Cayley Graph Of A Span Of Permutations)

Let $X$ be a set. Let $S$ be a set of permutations of $X$. Then a Cayley graph of $H=\text{span} (S)$ generated by $S$, which we'll write as $(H,S)$, is a colored directed graph that satisfies the the following three properties:

1. The vertex set is $\text{span} (S)$. Each vertex corresponds to a permutation.
2. Each element $s \in S$ is assigned a unique color which we'll denote by $c_s$.
3. For each color $c_s$, and each vertex $\sigma$, we draw the colored arrow $(\sigma ,s \circ \sigma)$.

Most of the time we assume that $S$ does not contain the identity. However, if it does contain the identity, then we just draw a colored loop $(\sigma,\sigma)$ at each vertex.

Problem 29 (Cayley Graph Patterns)

In each scenario below, you should draw a Cayley graph.

1. Let $X=\mathbb{Z}$, an infinite set. Consider the permutation $\phi_1:\mathbb{Z}\to \mathbb{Z}$ defined by $\phi_1(x)=x+1$. This permutation shifts elements in $\mathbb{Z}$ right one, with no wrap around. If we let $S=\{\phi_1\}$, give a rough sketch of the Cayley graph of $\text{span}(S)$. It's a rough sketch of the graph because there are infinitely many vertices.
2. How would you change your graph in part 1 if instead you used $S=\{\phi_2,\phi_3\}$, where these are shifts right 2 and 3 respectively?
3. Suppose that $X$ is a set, and that $S$ contains a single automorphism $s$ of $X$. Suppose also that we know $s^6$ is the identity (so following the arrow colored $c_s$ 6 times will return us to where we started). Construct a Cayley graph of $\text{span}(S)$. Is there more than one right answer to this?
4. Suppose that we know $S$ contains two elements $a$ and $b$. We also know that $a^2$ and $b^4$ are both the identity. In addition, we know that $a\circ b=b\circ a$, so if we start somewhere and follow the arrows colored $c_a$ and then $c_b$, then we should end up at the same place if we followed the arrows colored $c_b$ and then $c_a$. Construct a graph that satisfies these relationships. We'll often write this as $$\left<a,b\mid a^2=id, b^4=id, a\circ b=b\circ a\right>.$$

For more problems, see AllProblems