



Presentations
Pacing Tracker
- The quizzes have included questions for 16 objectives. How many have you passed? What are you plans to master those that you haven't mastered yet?
- We've finished units 1 through 3. Have you started your self-directed learning project for each unit?
- Remember you can submit only one SDL project per week. Plan ahead and don't let yourself get behind.
Brain Gains

- For the function $f(x,y) = x^2y^4$, we have $\vec \nabla f(x,y) = (2xy^4,4x^2y^3)$. Compute the differential of $\vec \nabla f(x,y)$, and then state the second derivative $D^2f(x,y)$.
Solution
We have $$\begin{align} d(\vec\nabla f) &= d(2xy^4,4x^2y^3)\\ &= ((2dx)y^4+2x(4y^3dy),(8xdx)y^3+4x^2(3y^2dy))\\ &= \begin{pmatrix}(2)y^4\\(8x)y^3\end{pmatrix}dx+\begin{pmatrix}2x(4y^3)\\4x^2(3y^2)\end{pmatrix}dy\\ &= \begin{bmatrix}(2)y^4&2x(4y^3)\\(8x)y^3&4x^2(3y^2)\end{bmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}. \end{align}$$ The last two lines above give the differential of $\vec \nabla f$ as a linear combination of partial derivatives, and then as a matrix product. The last line show the second derivative of $f$ is $$D^2f(x,y) = \begin{bmatrix}(2)y^4&2x(4y^3)\\(8x)y^3&4x^2(3y^2)\end{bmatrix} = \begin{bmatrix}2y^4&8xy^3\\8xy^3&12x^2y^2\end{bmatrix} .$$ We can also obtain this matrix by just directly computing all the second partial derivatives.
- $f_x = 2xy^4$ which means $f_{xx} = 2y^4$ and $f_{xy} = 8xy^3$. These form the first column.
- $f_y = 4x^2y^3$ which means $f_{yx} = 8xy^3$ and $f_{yy} = 12x^2y^2$. These form the second column.
- Use the figure below to answer a few questions related to directional derivatives.
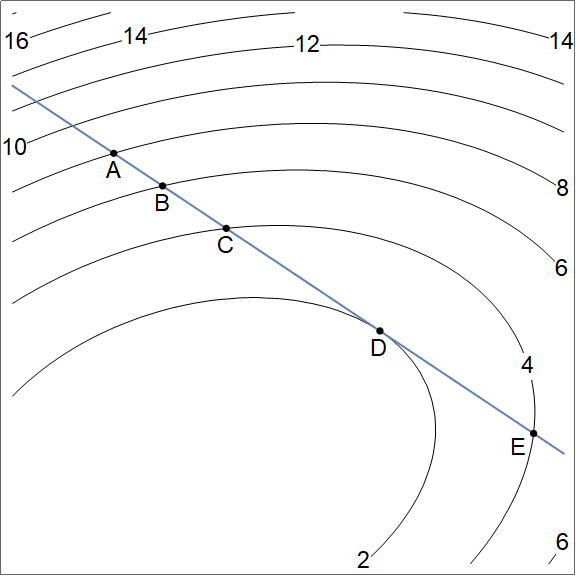
- List the following in decreasing order: $D_{\vec {BC}}f(A)$, $D_{\vec {BC}}f(B)$, $D_{\vec {BC}}f(C)$, $D_{\vec {BC}}f(D)$, $D_{\vec {BC}}f(E)$.
Solution
Notice that the direction $\vec{BC}$ is the same for each directional derivative. So all we really need to do is compare the slopes in the "south-east" direction at each of the 5 points.
- Because the contours have labels on them, we see that moving from $A$ to $B$ results in drop, so a negative slope. This is true at $A$, $B$, and $C$.
- Because the distance to level curves increases as we move south east starting at $A$, we can tell that the slope is most negative at $A$.
- At $D$ the slope is zero in the $\vec{BC}$ direction.
- At $E$ the slope is positive.
Ordering them in decreasing order gives $$D_{\vec {BC}}f(E) > D_{\vec {BC}}f(D) > D_{\vec {BC}}f(C) > D_{\vec {BC}}f(B) > D_{\vec {BC}}f(A).$$
- List the following in decreasing order: $D_{\vec {AB}}f(B)$, $D_{\vec {BC}}f(B)$, $D_{\vec {CD}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
Notice that the point $B$ is the exact same in each of these. Also notice that $\vec {AB}$, $\vec {BC}$, $\vec {CD}$, and $\vec{DE}$ all point in the same southeast direction (they have the same unit vector). Since $D_{\vec u}f(P) = \vec \nabla f(P)\cdot\frac{\vec u}{|\vec u|}$, these quantities are all equal. The unit direction is the same, and the point is the same, so the requested slopes are equal. This gives $$D_{\vec {AB}}f(B) = D_{\vec {BC}}f(B) = D_{\vec {CD}}f(B) = D_{\vec {DE}}f(B).$$
- List the following in decreasing order: $D_{\vec {DC}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
The direction $\vec {DC}$ is northwest, while the direction $\vec{DE}$ is southeast. Standing at point $B$, moving southeast results in a drop in height while moving northwest results in an increase in height. As such, we have $$D_{\vec {DC}}f(B) > D_{\vec {DE}}f(B).$$ We can actually say more in this problem Because the point is the same, and the directions are opposite, we know they are equal and opposite, giving us $$D_{\vec {DC}}f(B) = - D_{\vec {DE}}f(B).$$
- Suppose a plane passes through the point $(a,b,c)$ and has normal vector $(A,B,C)$. Give an equation of that plane.
Solution
If $Q = (x,y,z)$ is any other point on the plane, then $\vec {PQ} = (x-a,y-b,z-c)$ is a vector in the plane. Since $\vec n = (A,B,C)$ is normal to the plane, then we know $\vec n$ and $\vec {PQ}$ are orthogonal, which means $\vec n\cdot \vec {PQ}=0$. This gives an equation of the plane as $$(A,B,C)\cdot (x-a,y-b,z-c)=0\quad\text{or}\quad A(x-a)+B(y-b)+C(z-c)=0.$$
Group problems
- Give an equation of the tangent plane to $f(x,y)=x^2+4xy+3y^2$ at the point $(2,1)$.
- Verify that you obtain $$ \underbrace{z-15}_{dz} = \underbrace{(2(2)+4(1))}_{f_x(2,1)}\underbrace{(x-2)}_{dx}+\underbrace{(4(2)+6(1))}_{f_y(2,1)}\underbrace{(y-1)}_{dy} \quad \text{or} \quad z-15 = 8(x-2)+14(y-1) .$$
- For the function $f(x,y)=x^2+4xy+3y^2-10x-18y$, verify that the first derivative $Df(x,y)$ and second derivative $D^2f(x,y)$ are $$Df(x,y) = \begin{bmatrix}2x+4y-10&4x+6y-18\end{bmatrix}\quad\text{and}\quad
D^2f(x,y) = \begin{bmatrix}\begin{matrix}2\\4\end{matrix}&\begin{matrix}4\\6\end{matrix}\end{bmatrix}.
$$
- Solve $Df(x,y)=\begin{bmatrix}0&0\end{bmatrix}$, to find the critical points of this function. [Check: $(x,y)=(3,1)$.]
- Find the eigenvalues of $D^2f(3,1)$. [Check: $\lambda = 4\pm\sqrt{20} = 4\pm 2\sqrt{5}$.]
- Does the function $f$ have a local max, local min, or saddle at $(3,1)$? Explain.
- A rover travels along the path $2x-4y=12$. The elevation is given by $z=x+y^2-3$. Find the $(x,y)$ location of the lowest elevation reached by the rover along this path. [Check: $(x,y)=(4,-1)$ using Lagrange multipliers. Reminder: You need to identify
- $f(x,y)$ - the thing you wish to optimize
- $g(x,y)=c$ - the constraint.
- Then solve $\vec \nabla f = \lambda \vec \nabla g$ together with $g(x,y)=c$. ]
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$. [Check: $(-2)(x-(-3))+(-3)(y-(-2))+2(1)(z-1)=0$. ]
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$. [Check: $z-4 = (-1)^2(x-4)+2(4)(-1)(y-(-1))$.]
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
