



Presentations
5.21 - 5.28Pacing Tracker
- The quizzes have included questions for 22 objectives. How many have you passed? What are you plans to master those that you haven't mastered yet?
- We've finished units 1 through 4. Have you started your self-directed learning project for each unit?
- The 6th project can be over any topic from the entire semester. Feel free to get started on this one as soon as you have an idea.
- Remember you can submit only one SDL project per week. Plan ahead and don't let yourself get behind.
Brain Gains

- Fill in the blanks below, using the substitution $u=x^2$: $$\int_{3}^{7}xe^{x^2}dx = \int_{\_}^{49}e^{u}(\_)du .$$
Solution
$$\int_{3}^{7}xe^{x^2}dx = \int_{9}^{49}xe^{u}(\frac{1}{2x})du .$$
- Fill in the missing pieces below: $$\int_{0}^{3}\int_{0}^{\sqrt{9-x^2}}x dydx=\int_{?}^{?}\int_{?}^{?}(?)(?)drd\theta.$$
Solution
$$\int_{0}^{3}\int_{0}^{\sqrt{9-x^2}}x dydx=\int_{0}^{\pi/2}\int_{0}^{3}(r\cos\theta)(r)drd\theta.$$
- The points $P=(1,2,3)$ and $Q=(x,y,z)$ lie in a plane. A normal vector to this plane is $\vec n = (4,5,6)$. Give a single number for the dot product $\vec {PQ}\cdot \vec n$, in other words fill in the question mark below. $$4(x-1)+5(y-2)+6(z-3)=?$$
Solution
The vectors $\vec {PQ}$ and $\vec n$ are orthogonal so their dot product is zero. This gives $$4(x-1)+5(y-2)+6(z-3)=0,$$ which is an equation of the plane containing $P$ with normal vector $\vec n$.
- (Mentally complete - don't write the answer as it would take forever) For the curve $\vec r(t)=(4t^2, 5t-1,t^3)$, the velocity is $\vec v(t) =(8t,5,3t^2)$ and speed is $v(t) = \sqrt{(8t)^2+(5)^2+(3t^2)^2}$. A wire lies along this curve for $1\leq t\leq 4$, and has density function given by $\delta = xy$. Set up an integral that gives $\bar y$.
$$\bar y = \frac{\int_1^4(?)(?)(?)dt}{\int_1^4(?)(?)dt}$$
Solution
Remember that $ds = vdt = \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt$. We compute $$\begin{align} \bar y &=\frac{\int_C y dm}{\int_C dm}\\ &=\frac{\int_C y \delta ds}{\int_C \delta ds} \\ &=\frac{\int_C y (xy) ds}{\int_C (xy) ds} \\ &=\frac{\int_1^4 (5t-1) (4t^2(5t-1)) \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt}{\int_1^4 (4t^2(5t-1)) \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt}. \end{align} $$
- For the change of coordinates $x = 2u+3v$ and $y=4u+5v$ we have $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix}2\\4\end{pmatrix}du+\begin{pmatrix}3\\5\end{pmatrix}dv.$$ What is the Jacobian of this transformation, in other words fill in the blank below: $$\iint_{R_{xy}} dxdy = \iint_{R_{uv}}(?)dudv.$$
Solution
The Jacobian is the area of the parallelogram formed by the partial derivatives $(2,4)$ and $(3,5)$, namely $J=\dfrac{\partial(x,y)}{\partial(u,v)} = |2\cdot 5-3\cdot 4| = 2$. This means $$\iint_{R_{xy}} dxdy = \iint_{R_{uv}}(2)dudv.$$
- Find a nonzero vector that is orthogonal to both $(a,b,c)$ and $(d,e,f)$.
Solution
The cross product gives $(bf-ce, cd-af,ae-bd)$. Here are some ways to remember it.
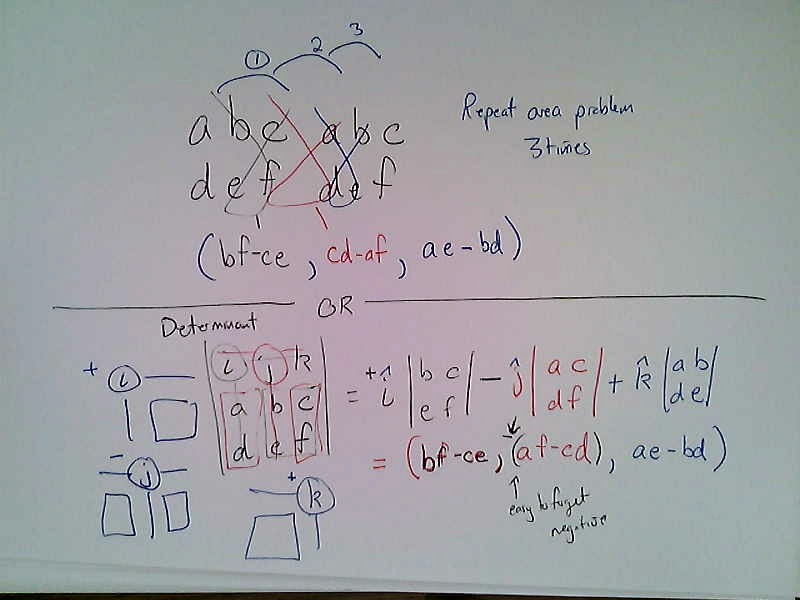
- Let $P=(a,b,c)$ be a point on a plane with normal vector $\vec n = (A,B,C)$. Let $Q=(x,y,z)$ be any other point on the same plane. Explain why $$A(x-a)+B(y-b)+C(z-c)=0.$$
Solution
Because $\vec {PQ}$ is a vector in the plane, and $\vec n$ is a normal vector to this plane, we know that two vectors meet at 90 degree angle. This means the dot product of $\vec n$ and $\vec {PQ}$ is equal to zero. This means an equation of a plane through $P=(a,b,c)$ with normal vector $\vec n = (A,B,C)$ is $$A(x-a)+B(y-c)+C(z-c)=0.$$
- Let $R=(1,0,0)$, $S = (2,0,-1)$, and $T = (0,1,3)$ be points on a plane. Find a normal vector to this plane, and then given an equation of the plane.
Solution
We can obtain a normal vector using the cross product $$\vec n =(1,0,-1)\times (-1,1,3) = \vec {RS}\times \vec {RT} = (1,-2,1).$$ An equation of the plane, using point $R$, is then $$(1)(x-1)+(-2)(y-0)+(1)(z-0)=0.$$ We can also use point $S$ or point $T$, obtaining $(1)(x-2)+(-2)(y-0)+(1)(z+1)=0$ or $(1)(x-0)+(-2)(y-1)+(1)(z-3)=0$. All three are equations of the same plane (just in a different form), and are all equivalent to $x-2y+z=1$.
Group problems
- Compute $\ds \int_{0}^{4}\int_{2x}^{8}e^{y^2}dydx$. [Hint: Draw the region and swap the order of integration.]
- For each region below, (1) set up a double integral that gives the area of the region. Feel free to use any coordinate system you want. Then set up a formula to compute $\bar x$, the $x$ coordinate of the centroid.
- The region in the first quadrant of the $xy$-plane that lies above the line $y=x$ and below the semicircle $y=\sqrt{16-x^2}$.
- The region in the first quadrant that lies below the line that passes through the two points $(4,0)$ and $(0,6)$.
- For each solid region below, (1) set up a triple integral that gives the volume of the region. Then set up a formula to compute $\bar z$, the $z$-coordinate of the centroid of the region.
- The solid hemiball of radius 3, above the $xy$-plane.
- The solid region in the first octant that lies under the paraboloid $z=9-x^2-y^2$.
- Set up an integral formula to compute each of the following:
- The mass of a disc that lies inside the circle $x^2+y^2=9$ and has density function given by $\delta = x+10$
- The $x$-coordinate of the center of mass (so $\bar x$) of the disc above.
- The $z$-coordinate of the center-of-mass (so $\bar z$) of the solid object in the first octant (all variables positive) that lies under the plane $2x+3y+6z=6$.
- The $y$-coordinate of the center-of-mass (so $\bar y$) of the same object.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
