



Presentations
4.8,15-21Pacing Tracker
- The quizzes have included questions for 16 objectives. How many have you passed? What are you plans to master those that you haven't mastered yet?
- We've finished units 1 through 3. Have you started your self-directed learning project for each unit?
- Remember you can submit only one SDL project per week. Plan ahead and don't let yourself get behind.
Brain Gains

- For the function $f(x,y)=x^2y^3$, compute $f_x$. Then compute the partial of $f_x$ with respect to $y$, which we write symbolically as $f_{xy}$, $(f_x)_y$, $\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)$, or $\frac{\partial^2 f}{\partial y\partial x}$.
Solution
We have $f_x = (2x)y^3$. We then compute the partial of this with respect to $y$ to obtain $f_{xy}=(2x)(3y^2)$.
- A parallelogram has edges given by the vectors $(2-e, 1)$ and $(3, 4-e)$. Find $e$ so that the area of the parallelogram is zero.
Solution
Remember the area formula $A=|ad-bc|$. Employing this formula gives $$ad-bc=(2-e)(4-e)-3 = (e^2-6e+8)-3 = e^2-6e+5 = (e-5)(e-1).$$ Since we want $A=0$, then we have either $e=5$ or $e=1$. We will soon call these "eigenvalues," and they will show up when looking at all 4 second partial derivatives.
- The image below shows a contour plot of a function $f$. Add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short.
Solution
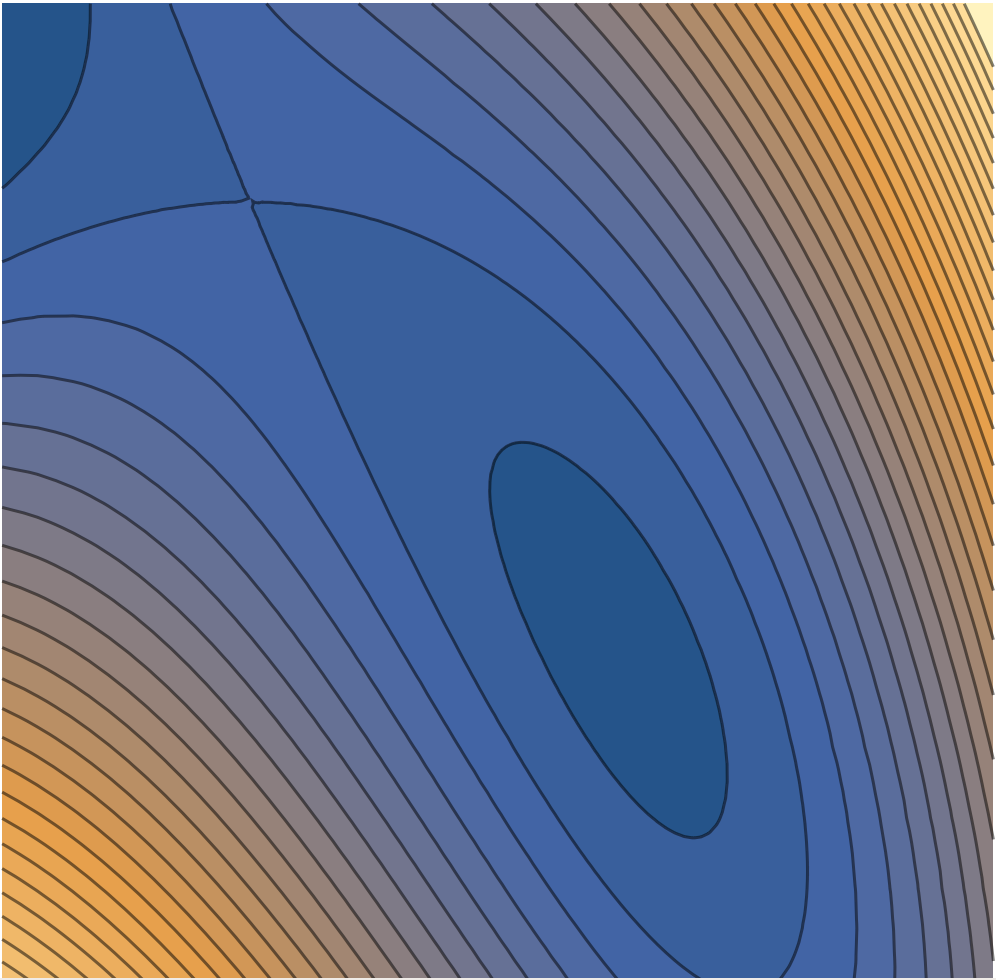
- The image below shows a plot of the gradient of a function $f$. Pick a vector, and then add a small bit of a contour line that would pass through the base of the vector. Repeat this several times, adding lots of little contours to your plot.
Solution

- Give an equation of the tangent line to $f(x) = x^2$ at $x=3$. Give your answer using point-slope form.
Solution
The equation is $y-9=6(x-3)$.
- Note that at $x=3$, we have $y=f(3) = 9$.
- The differential is $dy = 2xdx$.
- The change in $x$ along the tangent line from $(3,9)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,9)$ to $(x,y)$ is $dy = y-9$.
- Plugging $x=3$, $y=9$, $dx = x-3$, and $dy=y-9$ into the differential $dy = 2xdx$ gives $$\underbrace{dy}_{y-9}=\underbrace{2(3)}_{6}\underbrace{dx}_{x-3}.$$
- The hyperbola $x^2-y^2=5$ passes through the point $(3,2)$. Differentials tell us $2xdx-2ydy = 0$. Give an equation of the tangent line to this curve at $(3,2)$.
Solution
Let $(x,y)$ be a point on the tangent line.
- The change in $x$ along the tangent line from $(3,2)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,2)$ to $(x,y)$ is $dy=y-2$.
- Plugging $x=3$, $y=2$, $dx=x-3$ and $dy=y-2$ into the differential $2xdx-2ydy = 0$ gives the desired equation as $$2(\underbrace{3}_{x})\underbrace{ (x-3) }_{dx}-2(\underbrace{2}_{y})\underbrace{ (y-2) }_{dy} = 0.$$
- Find an $x$ value so that the two vectors $\vec u = 2{\bf i}+(3+x){\bf j}$ and $\vec v= 1{\bf i}+(2-x){\bf j}$ are parallel.
Solution
We need $(2,3+x) = \lambda (1,2-x)$ (one vector needs to be a multiple of the other). This gives two equations to solve, namely $$2=\lambda 1, \quad \text{and}\quad (3+x)=\lambda(2+x).$$ The first equation tells us $\lambda=2$. The second equation then becomes $3+x = 2(2-x)$, or $3+x=4-2x$. Rearranging gives $3x=1$, which means $x=1/3.$
Group problems
- We will find the points on the curve $g(x,y)=xy^2=16$ that minimize the function $f(x,y)=x^2+y^2$.
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- To find the points where $\vec \nabla f$ and $\vec \nabla g$ are either parallel or anti-parallel, we need to solve $\vec \nabla f=\lambda\vec \nabla g$ together with $g(x,y) = 16$. Write the three equations that result.
[Check: Did you get $2x=\lambda y^2$, $2y = \lambda 2xy$, and $xy^2=16$.
- Solve the system above. [Check: $x=2$ and $y=\pm \sqrt{8}=\pm 2\sqrt{2}$, $\lambda = $ something. ]
- Consider the function $f(x,y,z) = 4x^2+4y^2+z^2$. We'll be analyzing the surface at the point $P=(1/2,0,\sqrt{3})$.
- Compute $f(1/2,0,\sqrt{3})$.
- Draw the level surface that passes through $(1/2,0,\sqrt{3})$. So draw the ellipsoid $4=4x^2+4y^2+z^2$, which we can rewrite at $1=x^2+y^2+\frac{z^2}{4}$.
- Compute the gradient $\vec\nabla f(x,y,z)$, and then give $\vec\nabla f(P)$.
- Compute the differential $df$, and then the differential at $P$. [Check: For the latter, $df = 4dx+0dy+2\sqrt{3}dz$]
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1/2$, $dy=y-0$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane to the surface.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- Consider the function $f(x,y)=2-|x|$.
- Construct a 2D contour plot. Label your contours with their corresponding height.
- Construct a 3D surface plot.
- Construct both the above with software.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
