


Presenters
2PM
- 5.31 -
- 5.32 -
- 5.34 -
- 5.35 -
- 5.36 -
- 5.37 -
- 5.38 -
- 5.39 -
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.
Brain Gains (Rapid Recall)

- A plane passes through the point $P=(4,-2,-3)$. A normal vector to the plane is $\vec n = (-6,5,-7)$. Give an equation of the plane.
Solution
Let $Q=(x,y,z)$ be another point on the plane. This gives $$\vec{PQ}=(dx,dy,dz) = (x-4,y+2,z+3).$$ Since the vector $\vec n$ is a normal to the plane, then we know $\vec {PQ}$ and $\vec n$ are orthogonal, which gives us $\vec{PQ}\cdot \vec n=0$. This gives the equation $$(x-4,y+2,z+3)\cdot(-6,5,-7)=0$$ or $$-6(x-4)+5(y+2)-7(z+3)=0.$$
- Find the volume of a parallelepiped whose edges are the vectors $\vec u = (\cos\theta,\sin\theta,0)$, $\vec v = (-r\sin\theta,r\cos\theta,0)$ and $\vec w = (0,0,1)$. In other words, compute $|(\vec u\times\vec v)\cdot\vec w|$.
Solution
The cross product simplifies to $(0,0,r)$ after which the triple product gives $$|(0,0,r)\cdot(0,0,1)| =|r|.$$
- Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given, in cylindrical coordinates, by the iterated triple integral
$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$
Solution
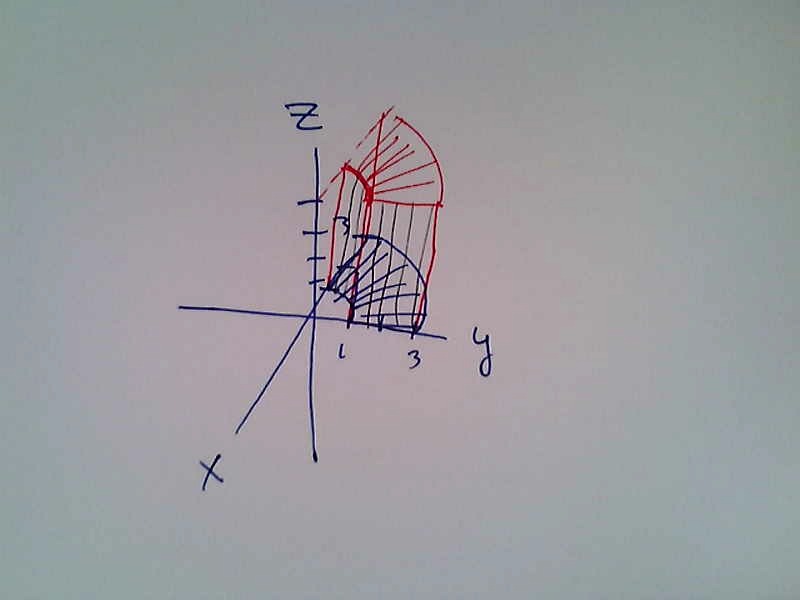
- Set up an integral formula to compute $\bar x$ for the solid above (use cylindrical coordinates).
Solution
No density is given, which means we interpret $\bar x$ as the $x$-coordinate of the centroid (so center of mass with $\delta=1$). This gives $$\bar x = \frac{\iiint_DxdV}{\iiint_DdV} = \frac{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}(r\cos\theta)rdz d\theta dr}{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr}.$$
- Give cylindrical equations for both the the sphere $x^2+y^2+z^2=9$ and paraboloid $z=9-x^2-y^2$.
Solution
Recall that $x^2+y^2=r^2$.
- An equation for the sphere is $r^2+z^2=9$.
- An equation for the paraboloid is $z=9-r^2$.
Group problems
- For each solid region below, set up a triple integral in cylindrical coordinates that gives the volume of the region. You can use Integration.nb to check if your bounds are correct.
- The solid hemiball of radius 3, above the $xy$-plane. [Check: One option is $\int_{0}^{3}\int_{0}^{\sqrt{9-r^2}}\int_{0}^{2\pi}rd\theta dzdr.$]
- The solid region in the first octant that lies under the paraboloid $z=9-x^2-y^2$.
- The solid region in the first octant that lies under the paraboloid $z=6-r^2$ and above the cone $z=r$. [Check: You should find the two surfaces intersect at $r=2$. One option is $\int_{0}^{2}\int_{?}^{6-r^2}\int_{0}^{?}rd\theta dzdr.$ I'll let you fill in the two question marks. ]
- (Cylindrical Coordinates - Disc and Shell method) This sequence of problems develops both the shell and disc method as by-products of cylindrical coordinates. The only difference is the order of integration. We'll use the solid region in space that is bounded above by $z=9-x^2-y^2$ (so $z=9-r^2$) and below by the $xy$-plane. In Cartesian coordinates, the volume of this region is given by $$\int_{-3}^{3}\int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}}\int_{0}^{9-x^2-y^2}dzdydx.$$ We now work with the region using cylindrical coordinates.
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta dzdr$. [Check: $\int_{0}^{3}\int_{0}^{9-r^2}\int_{0}^{2\pi}rd\theta dzdr.$ ]
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{3} 2\pi r (9-r^2) dr$. Recall the shell-method $$V = \int dV = \int_a^b \underbrace{(2\pi r)(\text{height of shell at $r$})}_{\text{shell surface area = (circumference)(height)}} \underbrace{dr}_{\text{shell thickness}}.$$
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta drdz$. You will end up with $r=\sqrt{9-z}$ as one of the bounds. You can use Integration.nb to check.
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{9} \pi (\sqrt{9-z})^2 dz$. Recall the disc-method $$V = \int dV =\int_a^b \underbrace{\pi (\text{radius of disc at height $z$})^2}_{\text{area of disc at height $z$}} \underbrace{dz}_{\text{little height}}.$$
- The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$. Remember that you can check if your bounds produce the correct solid with Integration.nb.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
