



9:00 AM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|
|
|
|
|
|
|
12:45 PM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 |
|
|
|
|
|
|
Presenters
9AM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 8am. If you upload something after that time, I may not see it.
- 5.19 - Nathan B
- 5.21 - Makenzy
- 5.23 - Ethan B
- 5.25 - As Class
- 5.26 - Next Time
- 5.27 -
- 5.28 -
- 5.29 -
12:45PM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 12 noon. If you upload something after that time, I may not see it.
- 5.21 -
- 5.23 -
- 5.24 - As class
- 5.25 - As class
- 5.26 - In Groups
- 5.27 -
- 5.28 -
- 5.29 -
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.

Brain Gains (Rapid Recall)
- Fill in the blanks below, using the substitution $u=x^2$: $$\int_{3}^{7}xe^{x^2}dx = \int_{\_}^{49}e^{u}(\_)du .$$
Solution
$$\int_{3}^{7}xe^{x^2}dx = \int_{9}^{49}xe^{u}(\frac{1}{2x})du .$$
- Fill in the missing pieces below: $$\int_{0}^{3}\int_{0}^{\sqrt{9-x^2}}x dydx=\int_{?}^{?}\int_{?}^{?}(?)(?)drd\theta.$$
Solution
$$\int_{0}^{3}\int_{0}^{\sqrt{9-x^2}}x dydx=\int_{0}^{\pi/2}\int_{0}^{3}(r\cos\theta)(r)drd\theta.$$
- The points $P=(1,2,3)$ and $Q=(x,y,z)$ lie in a plane. A normal vector to this plane is $\vec n = (4,5,6)$. Give a single number for the dot product $\vec {PQ}\cdot \vec n$, in other words fill in the question mark below. $$4(x-1)+5(y-2)+6(z-3)=?$$
Solution
The vectors $\vec {PQ}$ and $\vec n$ are orthogonal so their dot product is zero. This gives $$4(x-1)+5(y-2)+6(z-3)=0,$$ which is an equation of the plane containing $P$ with normal vector $\vec n$.
- (Mentally complete - don't write the answer as it would take forever) For the curve $\vec r(t)=(4t^2, 5t-1,t^3)$, the velocity is $\vec v(t) =(8t,5,3t^2)$ and speed is $v(t) = \sqrt{(8t)^2+(5)^2+(3t^2)^2}$. A wire lies along this curve for $1\leq t\leq 4$, and has density function given by $\delta = xy$. Set up an integral that gives $\bar y$.
$$\bar y = \frac{\int_1^4(?)(?)(?)dt}{\int_1^4(?)(?)dt}$$
Solution
Remember that $ds = vdt = \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt$. We compute $$\begin{align} \bar y &=\frac{\int_C y dm}{\int_C dm}\\ &=\frac{\int_C y \delta ds}{\int_C \delta ds} \\ &=\frac{\int_C y (xy) ds}{\int_C (xy) ds} \\ &=\frac{\int_1^4 (5t-1) (4t^2(5t-1)) \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt}{\int_1^4 (4t^2(5t-1)) \sqrt{(8t)^2+(5)^2+(3t^2)^2} dt}. \end{align} $$
- For the change of coordinates $x = 2u+3v$ and $y=4u+5v$ we have $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix}2\\4\end{pmatrix}du+\begin{pmatrix}3\\5\end{pmatrix}dv.$$ What is the Jacobian of this transformation, in other words fill in the blank below: $$\iint_{R_{xy}} dxdy = \iint_{R_{uv}}(?)dudv.$$
Solution
The Jacobian is the area of the parallelogram formed by the partial derivatives $(2,4)$ and $(3,5)$, namely $J=\dfrac{\partial(x,y)}{\partial(u,v)} = |2\cdot 5-3\cdot 4| = 2$. This means $$\iint_{R_{xy}} dxdy = \iint_{R_{uv}}(2)dudv.$$
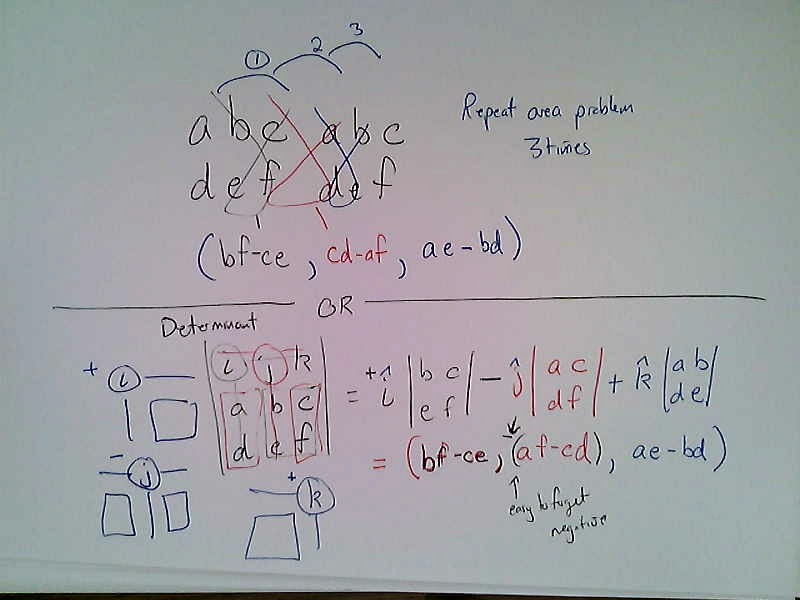
- Find a nonzero vector that is orthogonal to both $(a,b,c)$ and $(d,e,f)$.
Solution
The cross product gives $(bf-ce, cd-af,ae-bd)$. Here are some ways to remember it.
- Let $P=(a,b,c)$ be a point on a plane with normal vector $\vec n = (A,B,C)$. Let $Q=(x,y,z)$ be any other point on the same plane. Explain why $$A(x-a)+B(y-c)+C(z-c)=0.$$
Solution
Because $\vec {PQ}$ is a vector in the plane, and $\vec n$ is a normal vector to this plane, we know that two vectors meet at 90 degree angle. This means the dot product of $\vec n$ and $\vec {PQ}$ is equal to zero. This means an equation of a plane through $P=(a,b,c)$ with normal vector $\vec n = (A,B,C)$ is $$A(x-a)+B(y-c)+C(z-c)=0.$$
- Let $R=(1,0,0)$, $S = (2,0,-1)$, and $T = (0,1,3)$ be points on a plane. Find a normal vector to this plane, and then given an equation of the plane.
Solution
We can obtain a normal vector using the cross product $$\vec n =(1,0,-1)\times (-1,1,3) = \vec {RS}\times \vec {RT} = (1,-2,1).$$ An equation of the plane, using point $R$, is then $$(1)(x-1)+(-2)(y-0)+(1)(z-0)=0.$$ We can also use point $S$ or point $T$, obtaining $(1)(x-2)+(-2)(y-0)+(1)(z+1)=0$ or $(1)(x-0)+(-2)(y-1)+(1)(z-3)=0$. All three are equations of the same plane (just in a different form), and are all equivalent to $x-2y+z=1$.
Group problems
- Compute $\ds \int_{0}^{4}\int_{2x}^{8}e^{y^2}dydx$. [Hint: Draw the region and swap the order of integration.]
- For each region below, (1) set up a double integral that gives the area of the region. Feel free to use any coordinate system you want. Then set up a formula to compute $\bar x$, the $x$ coordinate of the centroid.
- The region in the first quadrant of the $xy$-plane that lies above the line $y=x$ and below the semicircle $y=\sqrt{16-x^2}$.
- The region in the first quadrant that lies below the line that passes through the two points $(4,0)$ and $(0,6)$.
- For each solid region below, (1) set up a triple integral that gives the volume of the region. Then set up a formula to compute $\bar z$, the $z$-coordinate of the centroid of the region.
- The solid hemiball of radius 3, above the $xy$-plane.
- The solid region in the first octant that lies under the paraboloid $z=9-x^2-y^2$.
- Set up an integral formula to compute each of the following:
- The mass of a disc that lies inside the circle $x^2+y^2=9$ and has density function given by $\delta = x+10$
- The $x$-coordinate of the center of mass (so $\bar x$) of the disc above.
- The $z$-coordinate of the center-of-mass (so $\bar z$) of the solid object in the first octant (all variables positive) that lies under the plane $2x+3y+6z=6$.
- The $y$-coordinate of the center-of-mass (so $\bar y$) of the same object.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
