



9:00 AM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|
|
|
|
|
|
|
12:45 PM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 |
|
|
|
|
|
|
Presenters
9AM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 8am. If you upload something after that time, I may not see it.
- 4.28 -
- 4.29 - Marissa
- 4.30 -
- 4.31 - Santiago
- 4.32 -
12:45PM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 12 noon. If you upload something after that time, I may not see it.
- 4.27 - Oscar
- 4.28 - Michael
- 4.29 - Trevor
- 4.30 - Alan
- 4.31 -
- 4.32 -
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.

Brain Gains (Rapid Recall)
- For the function $f(x,y) = x^2y^4$, we have $\vec \nabla f(x,y) = (2xy^4,4x^2y^3)$. Compute the differential of $\vec \nabla f(x,y)$, and then state the second derivative $D^2f(x,y)$.
Solution
We have $$\begin{align} d(\vec\nabla f) &= d(2xy^4,4x^2y^3)\\ &= ((2dx)y^4+2x(4y^3dy),(8xdx)y^3+4x^2(3y^2dy))\\ &= \begin{pmatrix}(2)y^4\\(8x)y^3\end{pmatrix}dx+\begin{pmatrix}2x(4y^3)\\4x^2(3y^2)\end{pmatrix}dy\\ &= \begin{bmatrix}(2)y^4&2x(4y^3)\\(8x)y^3&4x^2(3y^2)\end{bmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}. \end{align}$$ The last two lines above give the differential of $\vec \nabla f$ as a linear combination of partial derivatives, and then as a matrix product. The last line show the second derivative of $f$ is $$D^2f(x,y) = \begin{bmatrix}(2)y^4&2x(4y^3)\\(8x)y^3&4x^2(3y^2)\end{bmatrix} = \begin{bmatrix}2y^4&8xy^3\\8xy^3&12x^2y^2\end{bmatrix} .$$ We can also obtain this matrix by just directly computing all the second partial derivatives.
- $f_x = 2xy^4$ which means $f_{xx} = 2y^4$ and $f_{xy} = 8xy^3$. These form the first column.
- $f_y = 4x^2y^3$ which means $f_{yx} = 8xy^3$ and $f_{yy} = 12x^2y^2$. These form the second column.
- Use the figure below to answer a few questions related to directional derivatives.
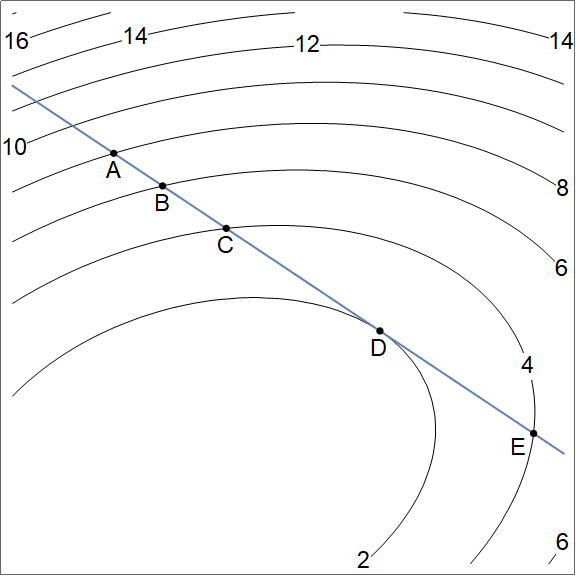
- List the following in decreasing order: $D_{\vec {BC}}f(A)$, $D_{\vec {BC}}f(B)$, $D_{\vec {BC}}f(C)$, $D_{\vec {BC}}f(D)$, $D_{\vec {BC}}f(E)$.
Solution
Notice that the direction $\vec{BC}$ is the same for each directional derivative. So all we really need to do is compare the slopes in the "south-east" direction at each of the 5 points.
- Because the contours have labels on them, we see that moving from $A$ to $B$ results in drop, so a negative slope. This is true at $A$, $B$, and $C$.
- Because the distance to level curves increases as we move south east starting at $A$, we can tell that the slope is most negative at $A$.
- At $D$ the slope is zero in the $\vec{BC}$ direction.
- At $E$ the slope is positive.
Ordering them in decreasing order gives $$D_{\vec {BC}}f(E) > D_{\vec {BC}}f(D) > D_{\vec {BC}}f(C) > D_{\vec {BC}}f(B) > D_{\vec {BC}}f(A).$$
- List the following in decreasing order: $D_{\vec {AB}}f(B)$, $D_{\vec {BC}}f(B)$, $D_{\vec {CD}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
Notice that the point $B$ is the exact same in each of these. Also notice that $\vec {AB}$, $\vec {BC}$, $\vec {CD}$, and $\vec{DE}$ all point in the same southeast direction (they have the same unit vector). Since $D_{\vec u}f(P) = \vec \nabla f(P)\cdot\frac{\vec u}{|\vec u|}$, these quantities are all equal. The unit direction is the same, and the point is the same, so the requested slopes are equal. This gives $$D_{\vec {AB}}f(B) = D_{\vec {BC}}f(B) = D_{\vec {CD}}f(B) = D_{\vec {DE}}f(B).$$
- List the following in decreasing order: $D_{\vec {DC}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
The direction $\vec {DC}$ is northwest, while the direction $\vec{DE}$ is southeast. Standing at point $B$, moving southeast results in a drop in height while moving northwest results in an increase in height. As such, we have $$D_{\vec {DC}}f(B) > D_{\vec {DE}}f(B).$$ We can actually say more in this problem Because the point is the same, and the directions are opposite, we know they are equal and opposite, giving us $$D_{\vec {DC}}f(B) = - D_{\vec {DE}}f(B).$$
- Suppose a plane passes through the point $(a,b,c)$ and has normal vector $(A,B,C)$. Give an equation of that plane.
Solution
If $Q = (x,y,z)$ is any other point on the plane, then $\vec {PQ} = (x-a,y-b,z-c)$ is a vector in the plane. Since $\vec n = (A,B,C)$ is normal to the plane, then we know $\vec n$ and $\vec {PQ}$ are orthogonal, which means $\vec n\cdot \vec {PQ}=0$. This gives an equation of the plane as $$(A,B,C)\cdot (x-a,y-b,z-c)=0\quad\text{or}\quad A(x-a)+B(y-b)+C(z-c)=0.$$
Group problems
- Give an equation of the tangent plane to $f(x,y)=x^2+4xy+3y^2$ at the point $(2,1)$.
- Verify that you obtain $$ \underbrace{z-15}_{dz} = \underbrace{(2(2)+4(1))}_{f_x(2,1)}\underbrace{(x-2)}_{dx}+\underbrace{(4(2)+6(1))}_{f_y(2,1)}\underbrace{(y-1)}_{dy} \quad \text{or} \quad z-15 = 8(x-2)+14(y-1) .$$
- For the function $f(x,y)=x^2+4xy+3y^2-10x-18y$, verify that the first derivative $Df(x,y)$ and second derivative $D^2f(x,y)$ are $$Df(x,y) = \begin{bmatrix}2x+4y-10&4x+6y-18\end{bmatrix}\quad\text{and}\quad
D^2f(x,y) = \begin{bmatrix}\begin{matrix}2\\4\end{matrix}&\begin{matrix}4\\6\end{matrix}\end{bmatrix}.
$$
- Solve $Df(x,y)=\begin{bmatrix}0&0\end{bmatrix}$, to find the critical points of this function. [Check: $(x,y)=(3,1)$.]
- Find the eigenvalues of $D^2f(3,1)$. [Check: $\lambda = 4\pm\sqrt{20} = 4\pm 2\sqrt{5}$.]
- Does the function $f$ have a local max, local min, or saddle at $(3,1)$? Explain.
- A rover travels along the path $2x-4y=12$. The elevation is given by $z=x+y^2-3$. Find the $(x,y)$ location of the lowest elevation reached by the rover along this path. [Check: $(x,y)=(4,-1)$ using Lagrange multipliers. Reminder: You need to identify
- $f(x,y)$ - the thing you wish to optimize
- $g(x,y)=c$ - the constraint.
- Then solve $\vec \nabla f = \lambda \vec \nabla g$ together with $g(x,y)=c$. ]
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$. [Check: $(-2)(x-(-3))+(-3)(y-(-2))+2(1)(z-1)=0$. ]
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$. [Check: $z-4 = (-1)^2(x-4)+2(4)(-1)(y-(-1))$.]
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
