



9:00 AM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|
|
|
|
|
|
|
12:45 PM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 |
|
|
|
|
|
|
Presenters
9AM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 8am. If you upload something after that time, I may not see it.
- 4.11 - Spencer B, Cecilia
- 4.16 - Tanner
- 4.17 - Denali
- 4.18 - Logan
- 4.19 - Kylar
- 4.20 -
- 4.21 -
- 4.22 -
12:45PM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 12 noon. If you upload something after that time, I may not see it.
- 4.11 - Hamilton
- 4.16 - Trevor
- 4.17 - Matty
- 4.18 - Forrest
- 4.19 -
- 4.20 -
- 4.21 -
- 4.22 -
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.

Brain Gains (Rapid Recall)
- Let $f(x,y)=ax+by$ and $\vec r(t) = (ct+d, et+f)$. Compute $\frac{df}{dt}$.
Solution
Two options:
- Substitute, so $f(\vec r(t)) = a(ct+d)+b(et+f)$, and then differentiate.
- Compute differentials, so $df=adx+bdy$, $dx=cdt$, and $dy=edt$, and then substitute.
Either way, we end up with $$\dfrac{df}{dt} = ac+be.$$ Symbolically, we have $$\frac{df}{dt} = \underbrace{a}_{f_x}\underbrace{c}_{\frac{dx}{dt}}+\underbrace{b}_{f_y}\underbrace{e}_{\frac{dy}{dt}} = f_x\frac{dx}{dt}+f_y\frac{dy}{dt}. $$ We call this the chain rule.
- For the function $f(x,y) = 4x^2y+y^3$, compute $f_x$ and $\ds\frac{\partial f}{\partial y}$.
Solution
We have
- $f_x = 8xy +0 $, and
- $\frac{\partial f}{\partial y} = 4x^2(1)+3y^2$.
- For the function $f(x,y) = 4x^2y+y^3$, compute $\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)$.
Solution
Since we know $\frac{\partial f}{\partial y} = 4x^2(1)+3y^2$, then we have $$\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) =\ds\frac{\partial}{\partial x}\left(4x^2(1)+3y^2\right) =8x. $$ We call the above the second partial derivative of f, first with respect to $y$, and then with respect to $x$. You'll see it appear in the homework very soon. For this function $f(x,y)$, there are four total second partial derivatives of $f$, namely $$ f_{xx}=\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right), \quad f_{xy}=\ds\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right), \quad f_{yx}=\ds\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right), \quad f_{yy}=\ds\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right). $$
- State $a$ and $b$ so that $\vec u=(-8,4,5)$ and $\vec v=(4,a,b)$ lie along the same line.
Solution
- $(4,-2,-\frac{5}{2})$.
- Consider the function $f(x,y)=y-x^2$. On a single $xy$-grid, graph the level curves with heights $0$, $1$, and $-4$. In other words, construct a contour plot that includes the contours 0, 1, -4.
Solution
- Your graph should have 3 parabolas, namely $y=x^2$, $y=x^2+1$, and $y=x^2-4$.
- Using the same function $f(x,y)=y-x^2$, construct a 3D surface plot.
Solution
- Your graph should have 3 parabolas, namely $y=x^2$, $y=x^2+1$, and $y=x^2-4$.
We'll look at these problems a bit later today, after you've practiced drawing together.
- If we know $\vec u\cdot \vec v=0$, then what is the angle between $\vec u$ and $\vec v$?
Solution
The vectors are orthogonal. So as long as neither is the zero vector, then the angle is 90 degrees.
- The image below shows a contour plot of a function $f$. Use Zoom's annotate tool to add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short.
Solution
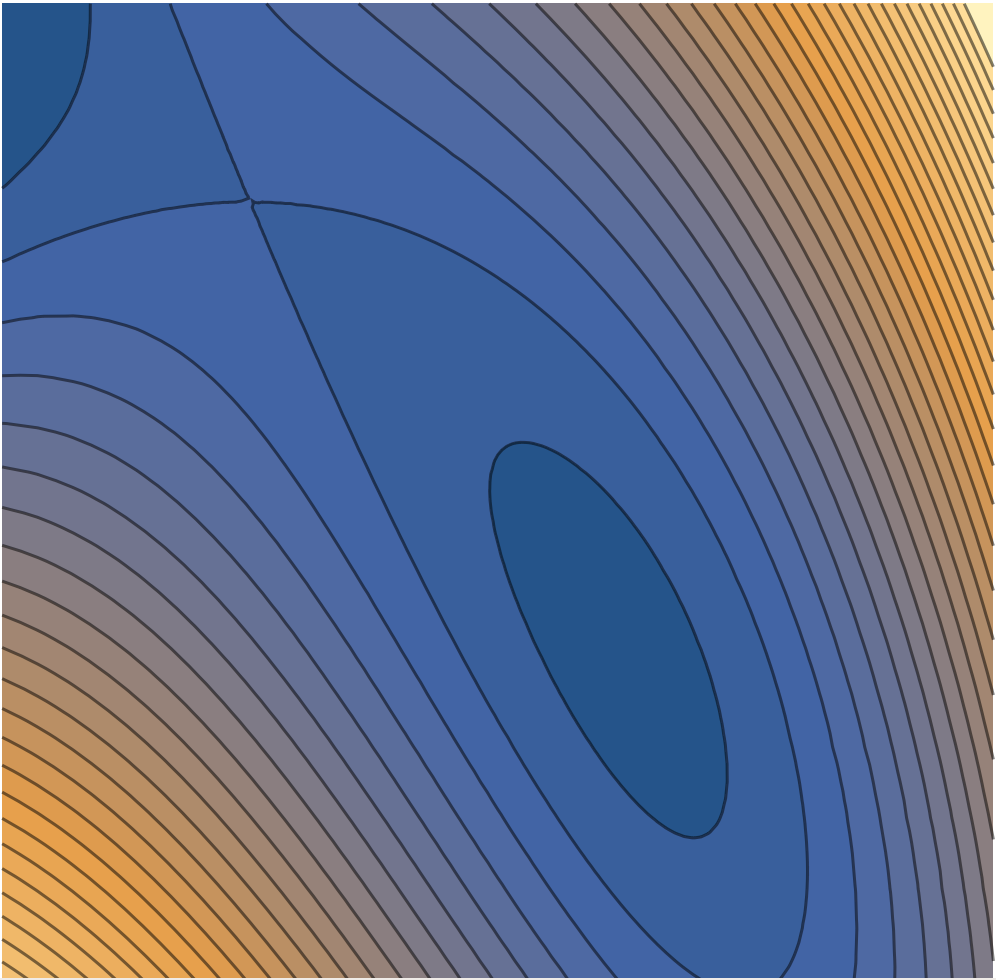
- The image below shows a plot of the gradient of a function $f$. Pick a vector, and then add a small bit of a contour line that would pass through the base of the vector.
Solution

Group problems
Here's a link to the Mathematica Notebook ContourSurfaceGradient.nb.
- Consider the function $z=4-y^2$.
- Construct a 2D contour plot by hand. So pick several values for $z$ and plot the resulting curves. If you end up with lots of horizontal lines in the $xy$-plane, you're doing this correctly. Write the height on each horizontal line you draw.
- Construct a 3D surface plot by hand.
- Construct both the above with software.
- Consider the function $f(x,y)=4-|x|$.
- Construct a 2D contour plot. Label your contours with their corresponding height.
- Construct a 3D surface plot.
- Construct both the above with software.
- As a group, open up the the problem set and discuss problem 4.20 together. If you finish 4.20 together, then start on 4.21. The link below will get you a PDF of the problem set.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
