



Rapid Recall
- A plane passes through the three points $P=(2,0,0)$, $Q=(0,3,0)$, and $R=(0,0,5)$. Find a vector $\vec n$ that is normal to this plane.
Solution
We need to find two vectors in the plane, and then cross them. One option is $\vec {PQ} = (-2,3,0)$ and $\vec {PR}= (-2,0,5)$. We then obtain $$ \vec {PQ}\times\vec {PR} =(15,10,6). $$
- A plane passes through the point $P=(4,-2,-3)$. A normal vector to the plane is $\vec n = (-6,5,-7)$. Give an equation of the plane.
Solution
Let $Q=(x,y,z)$ be another point on the plane. This gives $$\vec{PQ}=(dx,dy,dz) = (x-4,y+2,z+3).$$ Since the vector $\vec n$ is a normal to the plane, then we know $\vec {PQ}$ and $\vec n$ are orthogonal, which gives us $\vec{PQ}\cdot \vec n=0$. This gives the equation $$(x-4,y+2,z+3)\cdot(-6,5,-7)=0$$ or $$-6(x-4)+5(y+2)-7(z+3)=0.$$
- Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given by the iterated triple integral
$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$
Solution
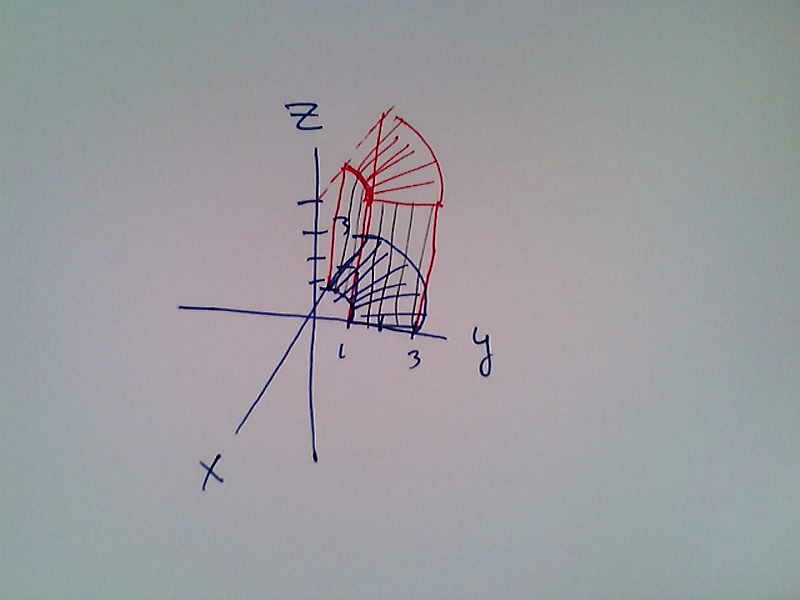
- Draw the region in space described by $1\leq r \leq 3$, $0\leq \theta \leq \pi$, $0\leq z\leq 4$.
- Set up an integral formula to compute $\bar x$ for the solid above.
Group problems
- Set up an integral formula to compute the $z$-coordinate of the center-of-mass (so $\bar z$) of the solid object in the first octant (all variables positive) that lies under the plane $2x+3y+6z=6$ (Draw the region as well).
- A wire lies along the curve $C$ parametrized by $\vec r(t) = (t^2+1, 3t, t^3)$ for $-1\leq t\leq 2$.
- Compute $ds$. (Remember - a little distance equals the product of the speed and a little time.)
- Set up an integral to find $\bar x$, then $\bar y$, then $\bar z$, for the centroid of $C$.
- Draw the region described the bounds of each integral.
- $\ds\int_{0}^{3}\int_{0}^{\pi}\int_{0}^{5}rdzd\theta dr$
- $\ds\int_{-1}^{1}\int_{0}^{1-y^2}\int_{0}^{x}dzdxdy$
- $\ds\int_{0}^{2}\int_{0}^{1-y/2}\int_{6+z}^{6-z}dxdzdy$
- Let $P=(1,2,0)$, $Q=(0,2,-1)$, and $R=(3,0,4)$.
- Find a vector that is orthogonal to both $\vec{PQ}$ and $\vec {PR}$.
- Find the area of triangle $\Delta PQR$.
- Give an equation of the plane PQR. (Let $S=(x,y,z)$ be any point on the plane PQR. Use $\vec {PS}\cdot (\vec {PQ}\times \vec {PR})=0$.)
- Let $T$ be another point in space. The quantity $\left|\text{proj}_{\vec {PQ}\times \vec {PR}}\vec {PT}\right|$ computes the distance between two things. What two things?
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
