Day 13 - Prep

Task 13.1

For the function $f(x,y) = 9-x^2-y^2$, we can compute the differential $df = -2xdx-2ydy$, the partial derivatives $f_x = -2x$ and $f_y=-2y$, along with the gradient $\vec \nabla f(x,y) = (-2x,-2y)$. Notice that the gradient is a vector field, so at the point $(x,y)$ we can draw the vector $(-2x,-2y)$.

1. Construct a plot of the vector field $\vec \nabla f(x,y) = (-2x,-2y)$.
2. Add to your vector field plot a contour plot of $f(x,y) = 9-x^2-y^2$ (we constructed a contour plot for the function in a previous Task).
3. What relationships do you see between the vectors from the gradient plot, and the level curves from your contour plot.

For the function $f(x,y) = x^2-y$, we can compute the differential $df = 2xdx-1dy$, the partial derivatives $f_x = 2x$ and $f_y=-1$, along with the gradient $\vec \nabla f(x,y) = (2x,-1)$. Again, notice that the gradient is a vector field, so at the point $(x,y)$ we can draw the vector $(2x,-1)$.

4. Construct a plot of the vector field $\vec \nabla f(x,y) = (2x,-1)$.
5. Add to your vector field plot a contour plot of $f(x,y) = x^2-y$ (we constructed a contour plot for the function in a previous Task).
6. What relationships do you see between the vectors from the gradient plot, and the level curves from your contour plot.

You can use the Mathematica file ContourSurfaceGradient.nb to check your work.

Task 13.2

Suppose the Mars rover Curiosity is currently on a hill, and its position is at the center of the map on the left below. Zooming in on the rover's position yields the map on the right below (the color legend applies to the graph on the right).

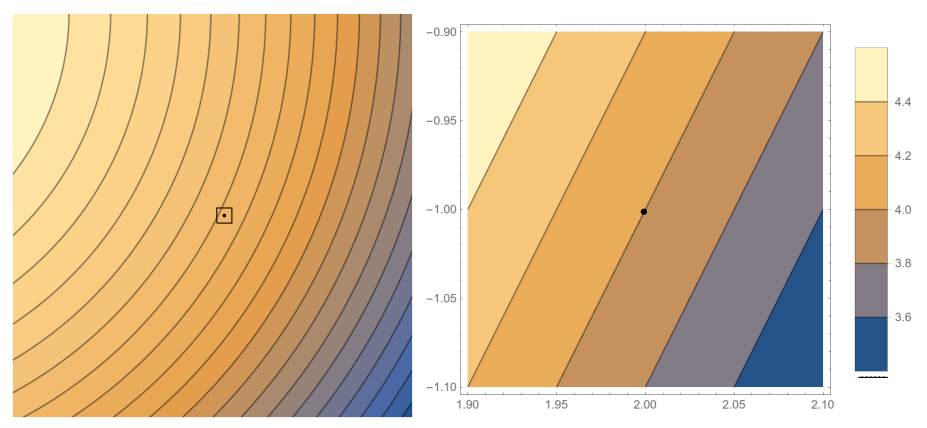
The contours in the graph to the right each represent a change in height of 0.2 units. The bounds for the graph are $1.9\leq x\leq 2.1$ and $-1.1\leq y\leq -0.9$. For simplicity of computations, let's assume the $x$, $y$ and $z$ axes use the same units. The rover is currently located at the point $(2,-1)$, shown as a dot.

The rover can head in many directions. In this problem we'll estimate the slope in several directions. For example, if the rover follows the vector $(0,1)$, heads north, then it has to move a distance (run) of $\Delta y = 0.1$ units to hit the next contour, resulting in a change in height of $\Delta z = +0.2$ units. This means the slope in the $(0,1)$ direction is $$\ds\frac{\text{rise}}{\text{run}} = \frac{\Delta z}{\text{distance moved in $xy$ plane}} = \frac{+0.2}{0.1} = 2.$$

1. Estimate the slope if the rover heads east, following $(1,0)$.
2. If the rover heads south, following $(0,-1)$, estimate the slope.
3. If the rover follows the direction $(1,1)$ (so northeast), what distance must the rover travel to hit the next contour? Use this to estimate the slope in the $(1,1)$ direction.
4. Estimate the slope in the $(1,2)$ direction.

Rather than starting with a contour plot and using it to visually estimate slopes, let's start with a function of the form $z=f(x,y)$ and use it to compute slopes. Suppose the elevation $z$ of terrain near the rover is given by the formula $z=f(x,y) = x^2+3xy$, and the rover is currently at $P=(2,-1)$.

5. Compute the differential $dz$ and write it in the form $dz = (?)dx+(?)dy$. Then evaluate $dz$ at the rover's location $P=(2,-1)$. [Check: Did you get $dz = (1)dx+(6)dy$?]
6. If the rover follows the direction $(dx,dy)$, explain why the slope is $\frac{dz}{\sqrt{(dx)^2+(dy)^2}}$.
7. Estimate the slope if the rover heads east, following $(dx,dy)=(1,0)$. Then estimate the slope if the rover heads north, following $(dx,dy)=(0,1)$. What do these values have to do with the partial derivatives of $f$?
8. Estimate the slope in the $(1,1)$ direction and then the $(1,2)$ direction.

Task 13.3

The volume of a right circular cylinder is $V(r,h)= \pi r^2 h$.

1. If we think of $h$ as a constant, so that $V(r)$ is only a function of $r$, then compute $\frac{dV}{dr}$.
2. If instead we think of $r$ as a constant, so that $V(h)$ is only a function of $h$, then compute $\frac{dV}{dh}$.
3. Compute the differential of $V(r,h)$, and then state the gradient $\vec \nabla V(r,h)$ along with the partial derivatives $\frac{\partial V}{\partial r}$ and $\frac{\partial V}{\partial h}$.
4. If we know $r=3$ and $h=4$, and we know that $r$ could increase by $dr=0.1$ and $h$ could increase by about $dh=0.2$, then use differentials to estimate how much $V$ will increase.

Notice that we were able to compute the partial derivatives above, without ever needing to compute the differential first. We obtain $\frac{\partial V}{\partial r}$ by imagining that every variable other than $r$ was a constant, and then computing the regular derivative.

5. The volume of a box is given by $f(x,y,z)=xyz$. Without computing the differential, compute $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, and $\frac{\partial f}{\partial z}$.
6. Now compute the differential $df$ (use implicit differentiation if needed) and verify that the partial derivatives you computed before actually show up in the differential $df$.
7. If the current measurements are $x=2$, $y=3$, and $z=5$, and we know that expected tolerances are $dx=.01$, $dy=.02$, and $dz=.03$, then estimate the change in volume.

Task 13.4

The last problem for prep each day will point to relevant problems from OpenStax. Spend 30 minutes working on problems from the sections below.

• section 4.3, exercises 118-131