Please Login to access more options.
Problem 18(Disjoint Cycle Notation Practice With Automorphisms Of A Square)
We have already shown that there are 8 automorphisms of the graph below.
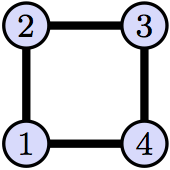
Write each of these automorphism using disjoint cycle notation. As an example, the automorphism that leaves 1 and 3 unchanged, but swaps 2 and 4, we write as $(1)(2,4)(3)$.
Solution
Consider the graph $\mathcal{G}=(V,E)$ drawn below (Figure 1). The vertex set is $V=\{1,2,3,4\}$ and edges $E=\{\{1,2\},\{2,3\},\{3,4\},\{1,4\}\}$.
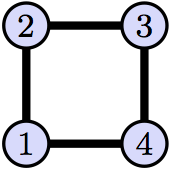
Figure 1: Graph $\mathcal{G}$.
From problem 6, the following table lists the automorphisms of the graph $\mathcal{G}$ in matrix notation.
$$ \begin{array}{|c|c|} \hline \text{Rotations} & \text{Flips}\\ \hline \begin{matrix} R_0=\begin{pmatrix} 1&2&3&4\\\ 1&2&3&4 \end{pmatrix} \\ R_{90}=\begin{pmatrix} 1&2&3&4\\\ 2&3&4&1 \end{pmatrix} \\ R_{180}=\begin{pmatrix} 1&2&3&4\\ 3&4&1&2 \end{pmatrix} \\ R_{270}= \begin{pmatrix} 1&2&3&4\\ 4&1&2&3 \end{pmatrix} \end{matrix} & \begin{matrix} H=\begin{pmatrix} 1&2&3&4\\ 2&1&4&3 \end{pmatrix} \\ V=\begin{pmatrix} 1&2&3&4\\ 4&3&2&1 \end{pmatrix} \\ D=\begin{pmatrix} 1&2&3&4\\ 3&2&1&4 \end{pmatrix} \\ D'=\begin{pmatrix} 1&2&3&4\\ 1&4&3&2 \end{pmatrix} \end{matrix} \\\hline \end{array} $$
Furthermore, the following table lists the automorphism of the graph $\mathcal{G}$ in disjoint cycle notation.
$$ \begin{array}{|c|c|} \hline \text{Rotations} & \text{Flips}\\ \hline \begin{matrix} R_{0}=() \\ R_{90}=(1,2,3,4) \\ R_{180}=(1,3)(2,4) \\ R_{270}=(1,4,3,2) \end{matrix} & \begin{matrix} H=(1,2)(3,4)\\ V=(1,4)(2,3)\\ D=(1,3)\\ D'=(2,4) \end{matrix} \\\hline \end{array} $$ This, is easily shown to be true by analyzing any one of the automorphisms $\sigma$ (written in matrix notation) of the graph $\mathcal{G}$. For example, consider $R_{90}$. If we perform the automorphism $R_{90}$ on each vertex of graph $\mathcal{G}$, we find that $R_{90}$ maps $1\rightarrow 2$, $2\rightarrow 3$, $3\rightarrow4$, and $4\rightarrow 1$. Thus, producing the automorphic cycle $1\rightarrow 2\rightarrow 3\rightarrow 4 \rightarrow 1 \rightarrow 2\rightarrow 3 ...$ which in disjoint cycle notation is written as (1,2,3,4). $\blacklozenge$
Tags
- When you are ready to submit this written work for grading, add the phrase [[!Submit]] to your page. This will tell me that you have completed the page (it's past rough draft form, and you believe it is in final draft form). Don't type [[!Submit]] on a rough draft.
- If I put [[!NeedsWork]] on your page, then your job is to review what I've written, address any comments made, and then delete all the comments I made. When you have finished reviewing your work, leave [[!NeedsWork]] on your page and type [[!Submit]]. (Both tags will show up). This tells me you have addressed the comments.
- I'll mark your work with [[!Complete]] after you have made appropriate revisions.
