Please Login to access more options.
Problem 19(Automorphisms On Several Graphs With 4 Vertices)
Consider the two graphs below.
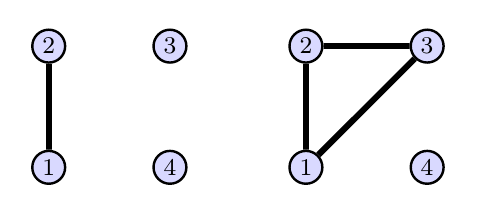
- For each graph, list the automorphisms of the graph. Use disjoint cycle notation to represent each automorphism.
- For each automorphism, state the smallest positive value of $k$ for which $\sigma^k$ is the identity automorphism. This is called the order of the automorphism.
- Construct another graph on 4 vertices different than the three we have seen so far. How many automorphisms does this graph have? Explain.
Solution
- For graph 1 we have 4 different automorphisms, which are (), (1,2), (3,4), and (1,2)(3,4). Note that there are no rotations listed. This is because a rotation would not preserve the edges. Because graph 2 has more edges we can get away a couple more automorphisms--namely (), (1,2,3), (1,3,2), (1,3), (2,3) and (1,2).
- We must now state the order of each automorphism. A reminder to the reader that the order of an automorphism is the smallest (positive) number of times that it can be applied to get back to the identity. We will construct a table to list the order of each permutation for each graph.
$$ \begin{array}{cc | cc} Graph 1 & & Graph2\\ Automorphism & Order & Automorphism & Order\\ \hline () & 1 & () & 1\\ (1,2) & 2 & (1,2) & 2\\ (3,4) & 2 & (1,3) & 2\\ (1,2)(3,4) & 2 & (2,3) & 2\\ & & (1,2,3) & 3\\ & & (1,3,2) & 3 \end{array} $$
- Now let us consider a different graph. Let us consider a graph with 4 vertices (similar to the ones shown above) with edges 1--3 and 2--4, so edges that connect cross elements. Interestingly enough, this graph will have 8 automorphisms just like the original graph with edges connecting all the corners (1--2, 2--3, 3--4, 4--1). All of the 8 possible permutations preserve the edges as well and as such are automorphisms of this new graph as well. If we wanted to construct a similar table for this new graph as for the other two graphs it would look something like the following.
$$ \begin{array}{cc} New Graph\\ Automorphism & Order\\ \hline () & 1\\ (1,3) & 2\\ (2,4) & 2\\ (1,2)(3,4) & 2\\ (1,3)(2,4) & 2\\ (1,4)(2,3) & 2\\ (1,4,3,2) & 4\\ (1,2,3,4) & 4\\ \end{array} $$
Tags
Change these as needed.
- When you are ready to submit this written work for grading, add the phrase [[!Submit]] to your page. This will tell me that you have completed the page (it's past rough draft form, and you believe it is in final draft form). Don't type [[!Submit]] on a rough draft.
- If I put [[!NeedsWork]] on your page, then your job is to review what I've written, address any comments made, and then delete all the comments I made. When you have finished reviewing your work, leave [[!NeedsWork]] on your page and type [[!Submit]]. (Both tags will show up). This tells me you have addressed the comments.
- I'll mark your work with [[!Complete]] after you have made appropriate revisions.
