Please Login to access more options.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
These are currently under construction.
Definition.Generating Sets for Groups
Let $G$ be a group. Let $S$ be a subset of $G$. We say that $G$ is generated by $S$ if for every $g\in G$, we can write $x$ in the form $x=a_1a_2a_3\cdots a_n$ where for each $i\in \{1,2,\ldots, n\}$ we have $a_i\in S$ or $a_i^{-1}\in S$.
Definition.Subgroup Generated by a Subset
Let $S$ be a subset of $G$. If $G$ is not generated by $S$, then we define the subgroup generated by $S$ to be the intersection of all subgroups of $G$ that contain $S$.
Problem.There are only two isomorphism classes of groups of order 4
Show that, up to isomorphism, there are only two groups of order 4. Do so by considering Cayley tables.
Definition.Equivalence Relation
Define equivalence relation (maybe)
Problem.Isomorphisms give an equivalence relation
Show that $\cong$ is an equivalence relation.
Problem. Subgroup Bonanza
Make a list of subgroups of Zn and/or U(n). Each time you make a subgroup, ask which group it is isomorphic to. We'll use this idea to build homomorphisms.
Definition. Cayley graph
We say that a colored digraph $\mathcal{G}=(V,C,E)$ is a Cayley graph if the following hold.
- For each $g\in V$ and each color $c\in C$, there is a single arrow $(g,x,c)$ from $g$ to $x$ that is colored by $c$. We'll use the notation $x=cg$ to say that starting at $g$ and then following the arrow colored $c$ leads us to $x$.
- For each $g\in V$ and each color $c\in C$, there is a single arrow $(y,g,c)$ from $y$ to $g$ that is colored by $c$. This means that $g=cy$ (starting at $y$ and following $c$ leads us to $g$). We'll use the notation $y=c^{-1}g$ to say that starting at $g$ and following backwards the arrow colored by $c$ leads us to $y$.
- The graph is connected, meaning given $x,y\in V$, we can start at vertex $x$ and then follow some sequence of colored arrows (either forwards or backwards) and eventually end at vertex $y$. Remember that the direction of the arrows does not matter for determining if the graph is connected.
- Pick a single vertex $v\in V$. For each $g\in V$, find a path from $v$ to $g$ which means we can write $g$ in the form $g=c_n^{i_n}\cdots c_2^{i_2}c_1^{i_1}v$ where each $i_k\in\{1,-1}$ and $c_k\in C$, in other words start at $v$ and find a path to $g$ that follows the color $c_1$ or works backwards along $c_1^{-1}$, and then follows the path $c_2$ or $c_2^{-1}$, etc. Once we have obtained such an expression for each vertex $g\in V$, then for each color $c\in C$ the function $f_c:V\to V$ defined by $f_c(g)=gc$ is an automorphism.
There are other ways to define a Cayley graph. If we start with a group and then construct the Cayley graph of a group using the generating set $S$, then it should be a Cayley graph. Let's prove this.
Problem.
Let $G$ be a group. Prove that the Cayley graph of $G$ generated by $S$ is indeed a Cayley graph.
Definition.Paths in Cayley Graphs
Suppose that $G$ is a group with generating set $S$, and we have construct the Cayley graph of $G$ generated by $S$.
- If $(x,y)$ is an arrow colored $s\in S$, then in the group we have $y=sx$ and $x=s^{-1}y$. We call this arrow a path of length 1 from $x$ to $y$.
- If $x,y\in G$, then a path from $x$ to $y$.... I need more here.
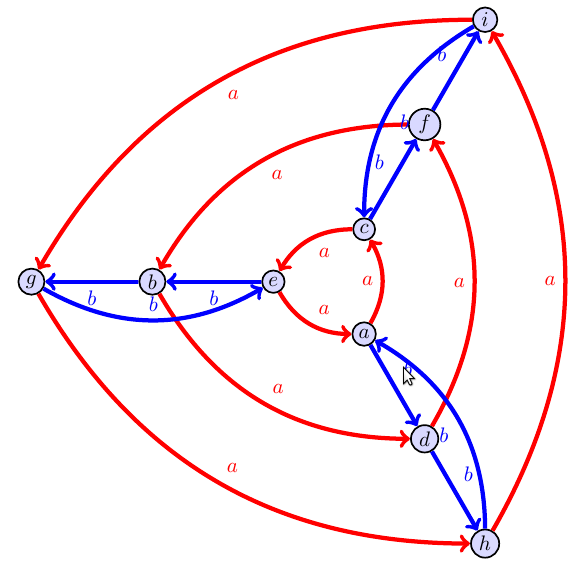
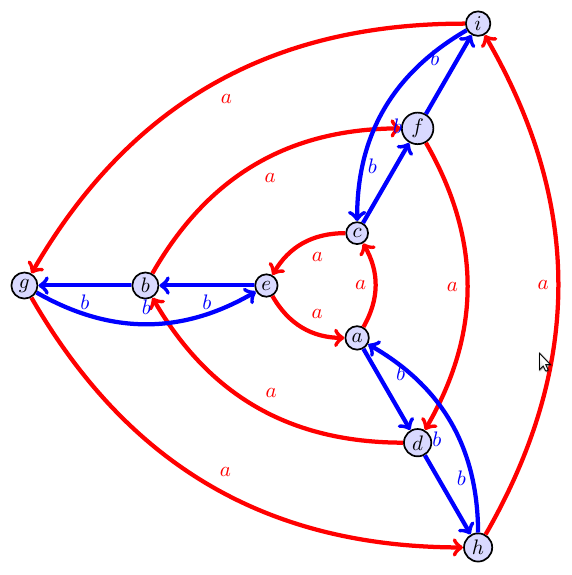
Problem.In Cayley Graphs, a closed path based at one point must be a closed path based at any other point
We've already seen earlier in the semester that the Cayley graph of a group looks the same from each point. If you were to stand at any point in the graph and look outwards, the same patterns you see at one point must always occur at every other point. So if you have a path (following a sequence of colored arrows, either forwards or backwards) that starts at $e$ and ends at $e$ (hence a closed path as the start and end points are the same, then if you started at another point $x$ and then followed this same closed path, you would have to arrive at $x$.
- In a Cayley graph, any closed path that starts at $x$ must also be a closed path
Use this idea to determine which of the graphs below is definitely not a Cayley graph. Then construct a multiplication table for the other.
Problem.Subgroups Generated by a Subset
I need a Cayley graph problem that has them develop the notion of a subgroup generated by a subset.
Problem.Practice With Cosets of The Integers
Let $G=\mathbb{Z}$ and let $H=n\mathbb{Z}$, the multiples of some integer $n$.
- For which $k$ does $k+H=H$? Make sure you justify your result.
- Prove that $i+H=j+H$ if and only if $i-j\in H$.
- If $m$ is an integer, then what is the smallest nonnegative integer $k$ so that $m+H=k+H$.
- If you consider the collection of cosets $S=\{k+H\mid k\in G\}$, then what is the cardinality of $S$?
Click to see a hint.
We have already proved that $a\pmod n = b\pmod n$ if and only if $a-b$ is a multiple of $n$. You should find yourself using quite often.
As an example, here's how a solution to part 1 could start.
- Let's show that $k+H=H$ if and only if $k$ is a multiple of $n$. Suppose first that $k+H=H$. Then since $0\in H$, we know that $k+0\in k+H$, and hence we must have $k\in H$ as $k+H=H$. This shows that $k$ is a multiple of $n$, i.e. $k\pmod n=0$. Now suppose instead that $k$ is a multiple of $n$. Then if $a\in k+H$ we must have $a=k+h$ where $h$ is a multiple of $n$. This means $a$ is the sum of two multiples of $n$, and hence $a\in H$ which shows that $k+H=H$. If we have $b\in H$, then since $b-k\in H$ we must
Since $H=\{qn\mid q\in \mathbb{Z}\}$, we know that $k+H=\{k+qn\mid q\in \mathbb{Z}\}$. So we know $a\in k+H$ if and only if $a=k+qn$ for some $q\in \mathbb{Z}$, which is true if and only if $k=a-qn$ for some $q\in \mathbb{Z}$. We then know that $k=a-qn$ for some $q\in \mathbb{Z}$ if and only if $a$ is a multiple of $n$.
For example, if we know that $k+H=H$, then we know that $k$ plus any multiple of $n$ is a multiple of $n$, so we then have. In fact, one of the lines above is actually this theorem precisely. This problem is here to help you practice with the set product notation $aH$ and $Ha$ (so cosets), or in this case $a+H$ as the group operation is addition.
Problem.
Prove that the subgroup generated by a subset $S$ is a subgroup.
Problem.Maps between $U(n)$ and $U(d)$.
Let $d$ be a divisor of an integer $n\geq 2$. Consider the maps $f:U(n)\to U(d)$ and $g:U(d)\to U(n)$ defined by $f(x)=x\pmod d$ and $g(x)=x\pmod n$.
- If $f$ is a homomorphism, then what equation must be true? (If you find yourself placing lots of parenthesis around mod $n$ and mod $d$ statements, you're doing this right.)
- If $g$ is a homomorphism, then what equation must be true?
- One of these maps is always a homomorphism, while the other might not be. Which is which? Prove your claims.
For more problems, see AllProblems
