



Presentations
5.? - 5.?Pacing Tracker
- The quizzes have included questions for 22 objectives. How many have you passed? What are you plans to master those that you haven't mastered yet?
- We've finished units 1 through 4. Have you started your self-directed learning project for each unit?
- The 6th project can be over any topic from the entire semester. Feel free to get started on this one as soon as you have an idea.
- Remember you can submit only one SDL project per week. Plan ahead and don't let yourself get behind.
Brain Gains

- A plane passes through the point $P=(4,-2,-3)$. A normal vector to the plane is $\vec n = (-6,5,-7)$. Give an equation of the plane.
Solution
Let $Q=(x,y,z)$ be another point on the plane. This gives $$\vec{PQ}=(dx,dy,dz) = (x-4,y+2,z+3).$$ Since the vector $\vec n$ is a normal to the plane, then we know $\vec {PQ}$ and $\vec n$ are orthogonal, which gives us $\vec{PQ}\cdot \vec n=0$. This gives the equation $$(x-4,y+2,z+3)\cdot(-6,5,-7)=0$$ or $$-6(x-4)+5(y+2)-7(z+3)=0.$$
- Find the volume of a parallelepiped whose edges are the vectors $\vec u = (\cos\theta,\sin\theta,0)$, $\vec v = (-r\sin\theta,r\cos\theta,0)$ and $\vec w = (0,0,1)$. In other words, compute $|(\vec u\times\vec v)\cdot\vec w|$.
Solution
The cross product simplifies to $(0,0,r)$ after which the triple product gives $$|(0,0,r)\cdot(0,0,1)| =|r|.$$
- Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given, in cylindrical coordinates, by the iterated triple integral
$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$
Solution
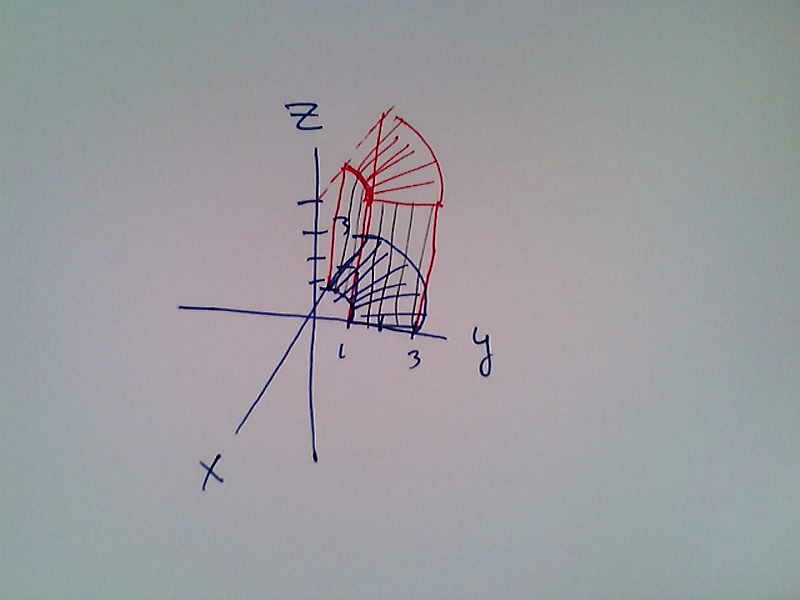
- Set up an integral formula to compute $\bar x$ for the solid above (use cylindrical coordinates).
Solution
No density is given, which means we interpret $\bar x$ as the $x$-coordinate of the centroid (so center of mass with $\delta=1$). This gives $$\bar x = \frac{\iiint_DxdV}{\iiint_DdV} = \frac{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}(r\cos\theta)rdz d\theta dr}{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr}.$$
- Give cylindrical equations for both the the sphere $x^2+y^2+z^2=9$ and paraboloid $z=9-x^2-y^2$.
Solution
Recall that $x^2+y^2=r^2$.
- An equation for the sphere is $r^2+z^2=9$.
- An equation for the paraboloid is $z=9-r^2$.
Group problems
- For each solid region below, set up a triple integral in cylindrical coordinates that gives the volume of the region. You can use Integration.nb to check if your bounds are correct.
- The solid hemiball of radius 3, above the $xy$-plane. [Check: One option is $\int_{0}^{3}\int_{0}^{\sqrt{9-r^2}}\int_{0}^{2\pi}rd\theta dzdr.$]
- The solid region in the first octant that lies under the paraboloid $z=9-x^2-y^2$.
- The solid region in the first octant that lies under the paraboloid $z=6-r^2$ and above the cone $z=r$. [Check: You should find the two surfaces intersect at $r=2$. One option is $\int_{0}^{2}\int_{?}^{6-r^2}\int_{0}^{?}rd\theta dzdr.$ I'll let you fill in the two question marks. ]
- (Cylindrical Coordinates - Disc and Shell method) This sequence of problems develops both the shell and disc method as by-products of cylindrical coordinates. The only difference is the order of integration. We'll use the solid region in space that is bounded above by $z=9-x^2-y^2$ (so $z=9-r^2$) and below by the $xy$-plane. In Cartesian coordinates, the volume of this region is given by $$\int_{-3}^{3}\int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}}\int_{0}^{9-x^2-y^2}dzdydx.$$ We now work with the region using cylindrical coordinates.
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta dzdr$. [Check: $\int_{0}^{3}\int_{0}^{9-r^2}\int_{0}^{2\pi}rd\theta dzdr.$ ]
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{3} 2\pi r (9-r^2) dr$. Recall the shell-method $$V = \int dV = \int_a^b \underbrace{(2\pi r)(\text{height of shell at $r$})}_{\text{shell surface area = (circumference)(height)}} \underbrace{dr}_{\text{shell thickness}}.$$
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta drdz$. You will end up with $r=\sqrt{9-z}$ as one of the bounds. You can use Integration.nb to check.
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{9} \pi (\sqrt{9-z})^2 dz$. Recall the disc-method $$V = \int dV =\int_a^b \underbrace{\pi (\text{radius of disc at height $z$})^2}_{\text{area of disc at height $z$}} \underbrace{dz}_{\text{little height}}.$$
- The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$. Remember that you can check if your bounds produce the correct solid with Integration.nb.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
