



Alternate Brain Gains
We're in catch up mode. Almost no one prepared work on Friday, so today we'll spend time in catch up mode. We'll tackle a problem in the Brain gains, then have someone share, then repeat. We may not have time for any group problems.
- Construct a contour plot of $f(x,y)=9-x^2-y^2$ which includes the contours $z=0$, $z=5$, and $z=8$. Then construct a surface plot that includes the vertical slices $y=0$ and $x=0$. (Similar to Problem 11.)
Solution
We'll draw this on the board, and then check using Mathematica.
f[x_, y_] := 9 - x^2 - y^2;
ContourPlot[f[x, y], {x, -4, 4}, {y, -4, 4}]
ContourPlot[f[x, y], {x, -4, 4}, {y, -4, 4}, Contours -> {0, 5, 8}]
Plot3D[f[x, y], {x, -4, 4}, {y, -4, 4}]
Plot3D[f[x, y], {x, -4, 4}, {y, -4, 4}, MeshFunctions -> {#3 &}]
- On the contour plot from the previous, add the path parametrized by $\vec r(t) = (2\cos t, 3\sin t)$. (Part of Problem 12.)
Solution
f[x_, y_] := 9 - x^2 - y^2;
r[t_] := {2 Cos[t], 3 Sin[t]};
p1 = ContourPlot[f[x, y], {x, -4, 4}, {y, -4, 4}];
p2 = ParametricPlot[r[t], {t, 0, 2 Pi}];
Show[p1, p2]
- With $f(x,y)=9-x^2-y^2$ and $\vec r(t) = (2\cos t, 3\sin t)$, use substitution to first state $f(\vec r(t))$, and then compute $\frac{df}{dt}$. (Part of Problem 13.)
Solution
Replacing $x=2\cos t$ and $y= 3\sin t$ gives $f(\vec r(t)) = 9-(2\cos t)^2-(3\sin t)^2$. The derivative is $$\frac{df}{dt} = -2(2\cos t)(-2\sin t)-2(3\sin t)(3\cos t).$$
- With $f(x,y)=9-x^2-y^2$ and $\vec r(t) = (2\cos t, 3\sin t)$, first compute the differential $df$ (in terms of $x$, $y$, $dx$, and $dy$) and then compute the differentials $dx$ and $dy$ in terms of $t$ and $dt$. Finish by stating $\frac{df}{dt}$. (Part of Problem 14.)
Solution
We have $df = -2x dx-2ydy$ with $dx = -2\sin t dt$ and $dy=3\cos t dt$. Substitution yields $$df = -2(2\cos t)(-2\sin t dt)-2(3\sin t)(3\cos t dt).$$ Division by $dt$ yields the value of $df/dt$, which matches the previous problem.
The chain rules states that you can substitute then differentiate, or you can differentiate and the substitute, and the result will be the same.
- We know in general that $df =\frac{\partial f}{\partial x} dx+\frac{\partial f}{\partial y} dy$. Explain why $\frac{df}{dt} = \vec \nabla f\cdot \frac{d\vec r}{dt}$. (Part of Problem 15, and used in Problem 16.)
Solution
Divide both sides of $df =\frac{\partial f}{\partial x} dx+\frac{\partial f}{\partial y} dy$ by $dt$ to obtain $$\frac{df}{dt} =\frac{\partial f}{\partial x} \frac{dx}{dt}+\frac{\partial f}{\partial y} \frac{dy}{dt} = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\cdot(\frac{dx}{dt},\frac{dy}{dt}) = \vec \nabla f\cdot \frac{d\vec r}{dt}.$$ This result holds in an number of dimensions.
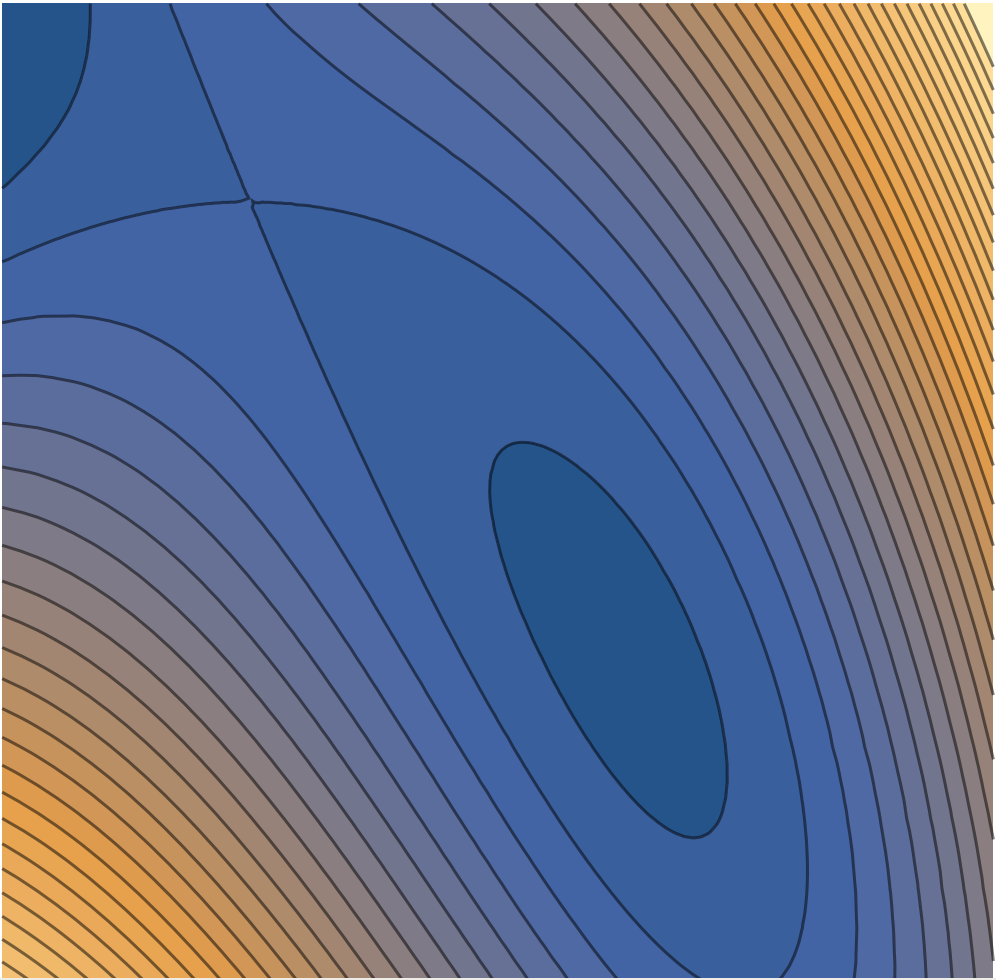
- The image below shows a contour plot of a function $f$. Add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short. (Similar to Problem 17.)
Solution
- The image below shows a plot of the gradient of a function $f$. Pick a vector, and then add a small bit of a contour line that would pass through the base of the vector. Repeat this several times, adding lots of little contours to your plot. (Similar to Problem 18.)
Solution

Presentations
Pacing Tracker
- The quizzes have included questions for 16 objectives. How many have you passed? What are you plans to master those that you haven't mastered yet?
- We've finished units 1 through 3. Have you started your self-directed learning project for each unit?
- Remember you can submit only one SDL project per week. Plan ahead and don't let yourself get behind.
Brain Gains

- For the function $f(x,y)=x^2y^3$, compute $f_x$. Then compute the partial of $f_x$ with respect to $y$, which we write symbolically as $f_{xy}$, $(f_x)_y$, $\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)$, or $\frac{\partial^2 f}{\partial y\partial x}$.
Solution
We have $f_x = (2x)y^3$. We then compute the partial of this with respect to $y$ to obtain $f_{xy}=(2x)(3y^2)$.
- A parallelogram has edges given by the vectors $(2-e, 1)$ and $(3, 4-e)$. Find $e$ so that the area of the parallelogram is zero.
Solution
Remember the area formula $A=|ad-bc|$. Employing this formula gives $$ad-bc=(2-e)(4-e)-3 = (e^2-6e+8)-3 = e^2-6e+5 = (e-5)(e-1).$$ Since we want $A=0$, then we have either $e=5$ or $e=1$. We will soon call these "eigenvalues," and they will show up when looking at all 4 second partial derivatives.
- The image below shows a contour plot of a function $f$. Add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short.
Solution

- The image below shows a plot of the gradient of a function $f$. Pick a vector, and then add a small bit of a contour line that would pass through the base of the vector. Repeat this several times, adding lots of little contours to your plot.
Solution

- Give an equation of the tangent line to $f(x) = x^2$ at $x=3$. Give your answer using point-slope form.
Solution
The equation is $y-9=6(x-3)$.
- Note that at $x=3$, we have $y=f(3) = 9$.
- The differential is $dy = 2xdx$.
- The change in $x$ along the tangent line from $(3,9)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,9)$ to $(x,y)$ is $dy = y-9$.
- Plugging $x=3$, $y=9$, $dx = x-3$, and $dy=y-9$ into the differential $dy = 2xdx$ gives $$\underbrace{dy}_{y-9}=\underbrace{2(3)}_{6}\underbrace{dx}_{x-3}.$$
- The hyperbola $x^2-y^2=5$ passes through the point $(3,2)$. Differentials tell us $2xdx-2ydy = 0$. Give an equation of the tangent line to this curve at $(3,2)$.
Solution
Let $(x,y)$ be a point on the tangent line.
- The change in $x$ along the tangent line from $(3,2)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,2)$ to $(x,y)$ is $dy=y-2$.
- Plugging $x=3$, $y=2$, $dx=x-3$ and $dy=y-2$ into the differential $2xdx-2ydy = 0$ gives the desired equation as $$2(\underbrace{3}_{x})\underbrace{ (x-3) }_{dx}-2(\underbrace{2}_{y})\underbrace{ (y-2) }_{dy} = 0.$$
- Find an $x$ value so that the two vectors $\vec u = 2{\bf i}+(3+x){\bf j}$ and $\vec v= 1{\bf i}+(2-x){\bf j}$ are parallel.
Solution
We need $(2,3+x) = \lambda (1,2-x)$ (one vector needs to be a multiple of the other). This gives two equations to solve, namely $$2=\lambda 1, \quad \text{and}\quad (3+x)=\lambda(2+x).$$ The first equation tells us $\lambda=2$. The second equation then becomes $3+x = 2(2-x)$, or $3+x=4-2x$. Rearranging gives $3x=1$, which means $x=1/3.$
Group problems
- We will find the points on the curve $g(x,y)=xy^2=16$ that minimize the function $f(x,y)=x^2+y^2$.
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- To find the points where $\vec \nabla f$ and $\vec \nabla g$ are either parallel or anti-parallel, we need to solve $\vec \nabla f=\lambda\vec \nabla g$ together with $g(x,y) = 16$. Write the three equations that result.
[Check: Did you get $2x=\lambda y^2$, $2y = \lambda 2xy$, and $xy^2=16$.
- Solve the system above. [Check: $x=2$ and $y=\pm \sqrt{8}=\pm 2\sqrt{2}$, $\lambda = $ something. ]
- Consider the function $f(x,y,z) = 4x^2+4y^2+z^2$. We'll be analyzing the surface at the point $P=(1/2,0,\sqrt{3})$.
- Compute $f(1/2,0,\sqrt{3})$.
- Draw the level surface that passes through $(1/2,0,\sqrt{3})$. So draw the ellipsoid $4=4x^2+4y^2+z^2$, which we can rewrite at $1=x^2+y^2+\frac{z^2}{4}$.
- Compute the gradient $\vec\nabla f(x,y,z)$, and then give $\vec\nabla f(P)$.
- Compute the differential $df$, and then the differential at $P$. [Check: For the latter, $df = 4dx+0dy+2\sqrt{3}dz$]
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1/2$, $dy=y-0$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane to the surface.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- Consider the function $f(x,y)=2-|x|$.
- Construct a 2D contour plot. Label your contours with their corresponding height.
- Construct a 3D surface plot.
- Construct both the above with software.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
