



9:00 AM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|
|
|
|
|
|
|
12:45 PM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 |
|
|
|
|
|
|
Presenters
9AM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 8am. If you upload something after that time, I may not see it.
- 5.32 - Next Time
- 5.34 - Next Time
- 5.35 - Next Time
- 5.36 - Next Time
- 5.37 - Next Time
- 5.38 - Next Time
- 5.39 - Next Time
12:45PM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 12 noon. If you upload something after that time, I may not see it.
- 5.32 - Next Time
- 5.34 - Next Time
- 5.35 - Next Time
- 5.36 - Next Time
- 5.37 - Next Time
- 5.38 - Next Time
- 5.39 - Next Time
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.

Brain Gains (Rapid Recall)
- Give the $(x,y,z)$ coordinates of the point in space whose spherical coordinates are $(\rho,\phi,\theta) = (3,\pi/2,\pi)$.
Solution
We're on a sphere of radius 3. The fact that $\rho=\pi/2$ means we've dropped 90 degrees from the positive $z$-axis, so we are in the $xy$-plane. With an angle of $\theta=\pi$, that puts us on the negative $x$-axis. The solution is $$(x,y,z)=(-3,0,0).$$
- Give $(\rho,\phi,\theta)$ coordinates for the Cartesian coordinates $(0,0,4)$, $(3,0,0)$, $(0,2,0)$, and $(0,0,-1)$.
Solution
A solution appears in the table below. When $\phi=0$ or $\phi=\pi$, the value of $\theta$ is arbitrary. You can of course add any multiple of $2\pi$ to any value of $\theta$ below, and still have a valid solution. $$\begin{array}{c|c} \text{Cartesian}&\text{Spherical}\\ (x,y,z)&(\rho,\phi,\theta)\\\hline (0,0,4)& (4,0,\text{any})\\ (3,0,0)& (3,\pi/2,0)\\ (0,2,0)& (2,\pi/2,\pi/2)\\ (0,0,-1)&(1,\pi,\text{any}) \end{array}$$
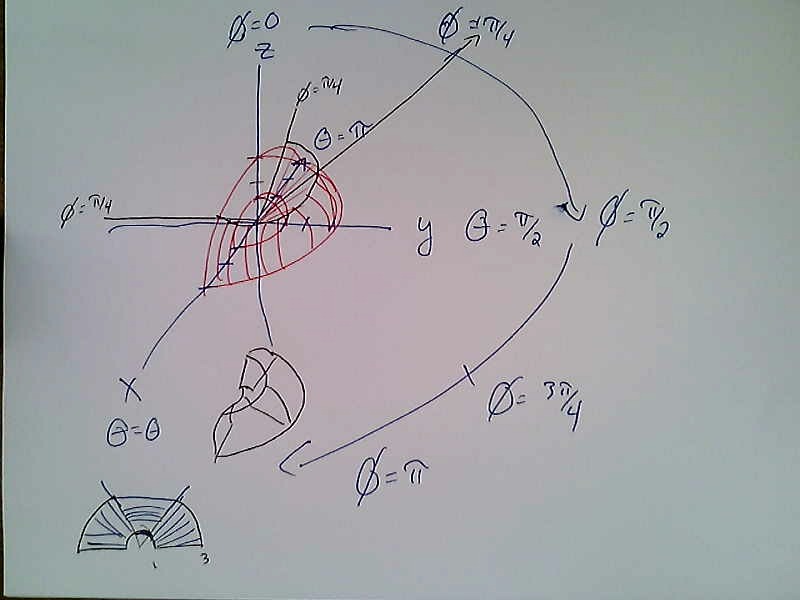
- Draw the region in space described by $1\leq \rho \leq 3$, $0\leq \theta \leq \pi$, and $\pi/4\leq \phi\leq \pi/2$.
Solution
- Set up an integral formula to compute $\bar z$ for the solid above. (Recall $\frac{\partial(x,y,z)}{\partial(\rho,\phi,\theta)} = |\rho^2\sin\phi|$ and $z=\rho\cos\phi$.)
Solution
With $dV =(\rho^2\sin\phi) d\rho d\phi d\theta$ and $z = \rho \cos \phi$, we have $$\bar z =\frac{\iiint_DzdV}{\iiint_DdV} = \frac{\int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{1}^{3}(\rho\cos\phi)(\rho^2\sin\phi) d\rho d\phi d\theta}{\int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{1}^{3}(\rho^2\sin\phi) d\rho d\phi d\theta}.$$
- A tennis ball has been cut in half. Suppose the inner radius of the tennis ball is 3 cm, and the outer radius is 3.5 cm. Give bounds of the form $?\leq \theta\leq ?$, $?\leq \phi\leq ?$, $?\leq \rho\leq ?$, to describe the bottom half ($z\leq 0$) of the tennis ball.
Solution
One option for the bounds is $0\leq \theta\leq 2\pi$, $\pi/2\leq \phi\leq \pi$, $3\leq \rho\leq 3.5$
Group problems
- The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$. Remember that you can check if your bounds produce the correct solid with Integration.nb.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$.
- (Cylindrical Coordinates - Disc and Shell method) This sequence of problems develops both the shell and disc method as by-products of cylindrical coordinates. The only difference is the order of integration. We'll use the solid region in space that is bounded above by $z=9-x^2-y^2$ (so $z=9-r^2$) and below by the $xy$-plane. In Cartesian coordinates, the volume of this region is given by $$\int_{-3}^{3}\int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}}\int_{0}^{9-x^2-y^2}dzdydx.$$ We now work with the region using cylindrical coordinates.
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta dzdr$. [Check: $\int_{0}^{3}\int_{0}^{9-r^2}\int_{0}^{2\pi}rd\theta dzdr.$ ]
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{3} 2\pi r (9-r^2) dr$. Recall the shell-method $$V = \int dV = \int_a^b \underbrace{(2\pi r)(\text{height of shell at $r$})}_{\text{shell surface area = (circumference)(height)}} \underbrace{dr}_{\text{shell thickness}}.$$
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta drdz$. You will end up with $r=\sqrt{9-z}$ as one of the bounds. You can use Integration.nb to check.
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{9} \pi (\sqrt{9-z})^2 dz$. Recall the disc-method $$V = \int dV =\int_a^b \underbrace{\pi (\text{radius of disc at height $z$})^2}_{\text{area of disc at height $z$}} \underbrace{dz}_{\text{little height}}.$$
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
