



9:00 AM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|
|
|
|
|
|
|
12:45 PM Jamboard Links
| G1 | G2 | G3 | G4 | G5 | G6 |
|
|
|
|
|
|
Presenters
9AM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 8am. If you upload something after that time, I may not see it.
- 4.18 - Logan
- 4.19 - Parker
- 4.20 - Tanner
- 4.21 - Santiago
- 4.22 - Ethan
- 4.23 - Makenzy, Kallan
- 4.24 -
- 4.25 -
12:45PM
Thanks for sharing things in Perusall. Here are the presenters for today. Remember, I start picking presenters at 12 noon. If you upload something after that time, I may not see it.
- 4.18 - Forrest
- 4.19 - Hamilton
- 4.20 - Joshua
- 4.21 - Alan
- 4.22 - Reed
- 4.23 -
- 4.24 -
- 4.25 -
Learning Reminders
- We are in the 13th week of the semester. If you are on track for an A, then ideally you're finishing your SDL project for the 5th unit, and proposed something for the 6th unit.
- There are only 2 weeks left, which means you can submit at most 2 more SDL projects.
- The final SDL project (6th) can be over any topic from the entire semester. You can use it to expand what we do in the 6th unit, or you may choose to revisit something from a prior unit that you would like to spend more time with.

Brain Gains (Rapid Recall)
- For the function $f(x,y)=x^2y^3$, compute $f_x$. Then compute the partial of $f_x$ with respect to $y$, which we write symbolically as $f_{xy}$, $(f_x)_y$, $\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)$, or $\frac{\partial^2 f}{\partial y\partial x}$.
Solution
We have $f_x = (2x)y^3$. We then compute the partial of this with respect to $y$ to obtain $f_{xy}=(2x)(3y^2)$.
- A parallelogram has edges given by the vectors $(2-e, 1)$ and $(3, 4-e)$. Find $e$ so that the area of the parallelogram is zero.
Solution
Remember the area formula $A=|ad-bc|$. Employing this formula gives $$ad-bc=(2-e)(4-e)-3 = (e^2-6e+8)-3 = e^2-6e+5 = (e-5)(e-1).$$ Since we want $A=0$, then we have either $e=5$ or $e=1$. We will soon call these "eigenvalues," and they will show up when looking at all 4 second partial derivatives.
- The image below shows a contour plot of a function $f$. Use Zoom's annotate tool to add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short.
Solution
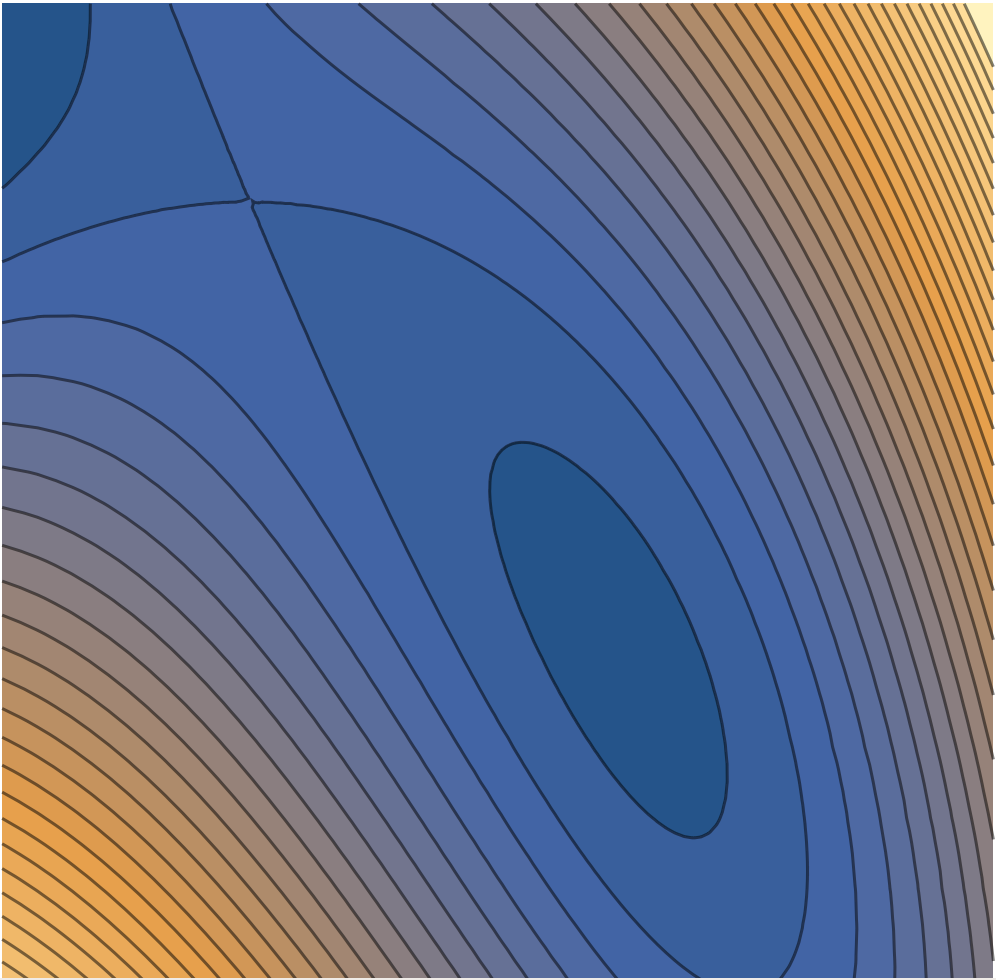
- The image below shows a plot of the gradient of a function $f$. Pick a vector, and then add a small bit of a contour line that would pass through the base of the vector.
Solution

- Give an equation of the tangent line to $f(x) = x^2$ at $x=3$. Give your answer using point-slope form.
Solution
The equation is $y-9=6(x-3)$.
- Note that at $x=3$, we have $y=f(3) = 9$.
- The differential is $dy = 2xdx$.
- The change in $x$ along the tangent line from $(3,9)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,9)$ to $(x,y)$ is $dy = y-9$.
- Plugging $x=3$, $y=9$, $dx = x-3$, and $dy=y-9$ into the differential $dy = 2xdx$ gives $$\underbrace{dy}_{y-9}=\underbrace{2(3)}_{6}\underbrace{dx}_{x-3}.$$
- The hyperbola $x^2-y^2=5$ passes through the point $(3,2)$. Differentials tell us $2xdx-2ydy = 0$. Give an equation of the tangent line to this curve at $(3,2)$.
Solution
Let $(x,y)$ be a point on the tangent line.
- The change in $x$ along the tangent line from $(3,2)$ to $(x,y)$ is $dx = x-3$.
- The change in $y$ along the tangent line from $(3,2)$ to $(x,y)$ is $dy=y-2$.
- Plugging $x=3$, $y=2$, $dx=x-3$ and $dy=y-2$ into the differential $2xdx-2ydy = 0$ gives the desired equation as $$2(\underbrace{3}_{x})\underbrace{ (x-3) }_{dx}-2(\underbrace{2}_{y})\underbrace{ (y-2) }_{dy} = 0.$$
- Find an $x$ value so that the two vectors $\vec u = 2{\bf i}+(3+x){\bf j}$ and $\vec v= 1{\bf i}+(2-x){\bf j}$ are parallel.
Solution
We need $(2,3+x) = \lambda (1,2-x)$ (one vector needs to be a multiple of the other). This gives two equations to solve, namely $$2=\lambda 1, \quad \text{and}\quad (3+x)=\lambda(2+x).$$ The first equation tells us $\lambda=2$. The second equation then becomes $3+x = 2(2-x)$, or $3+x=4-2x$. Rearranging gives $3x=1$, which means $x=1/3.$
Group problems
Here's a link to the Mathematica Notebook ContourSurfaceGradient.nb.
- We will find the points on the curve $g(x,y)=xy^2=16$ that minimize the function $f(x,y)=x^2+y^2$.
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- To find the points where $\vec \nabla f$ and $\vec \nabla g$ are either parallel or anti-parallel, we need to solve $\vec \nabla f=\lambda\vec \nabla g$ together with $g(x,y) = 16$. Write the three equations that result.
[Check: Did you get $2x=\lambda y^2$, $2y = \lambda 2xy$, and $xy^2=16$.
- Solve the system above. [Check: $x=2$ and $y=\pm \sqrt{8}=\pm 2\sqrt{2}$, $\lambda = $ something. ]
- Consider the function $f(x,y,z) = 4x^2+4y^2+z^2$. We'll be analyzing the surface at the point $P=(1/2,0,\sqrt{3})$.
- Compute $f(1/2,0,\sqrt{3})$.
- Draw the level surface that passes through $(1/2,0,\sqrt{3})$. So draw the ellipsoid $4=4x^2+4y^2+z^2$, which we can rewrite at $1=x^2+y^2+\frac{z^2}{4}$.
- Compute the gradient $\vec\nabla f(x,y,z)$, and then give $\vec\nabla f(P)$.
- Compute the differential $df$, and then the differential at $P$. [Check: For the latter, $df = 4dx+0dy+2\sqrt{3}dz$]
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1/2$, $dy=y-0$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane to the surface.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- Consider the function $f(x,y)=2-|x|$.
- Construct a 2D contour plot. Label your contours with their corresponding height.
- Construct a 3D surface plot.
- Construct both the above with software.
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
