



Schedule
Today
- 23 - Br. Woodruff
- 26 - Andrew
- 28 - Justin
- 29 - Br. Woodruff
- 30 - Chandler
- 31 - Next Time
- 32 - Next Time
- 33 - Br. Woodruff
Next time
- Please work on any of 31-39 (the end of the unit).
- We'll finish the unit up on Monday.
- Quiz will be open all weekend. Take it this weekend the first time.
- Exam on Tuesday/Wednesday
Rapid Recall
- Find the volume of a parallelepiped whose edges are the vectors $\vec u = (\cos\theta,\sin\theta,0)$, $\vec v = (-r\sin\theta,r\cos\theta,0)$ and $\vec w = (0,0,1)$. In other words, compute $|(\vec u\times\vec v)\cdot\vec w|$.
Solution
The solution is $|r|$.
- Give the $(x,y,z)$ coordinates of the point in space whose spherical coordinates are $(\rho,\phi,\theta) = (3,\pi/2,\pi)$.
Solution
We're on a sphere of radius 3. The fact that $\rho=\pi/2$ means we've dropped 90 degrees from the positive $z$-axis, so we are in the $xy$-plane. With an angle of $\theta=\pi$, that puts us on the negative $x$-axis. The solution is $(x,y,z)=(-3,0,0)$.
- Give $(\rho,\phi,\theta)$ coordinates for the Cartesian coordinates $(0,0,4)$, $(3,0,0)$, $(0,2,0)$, and $(0,0,-1)$.
Solution
We're on a sphere of radius 3. The fact that $\rho=\pi/2$ means we've dropped 90 degrees from the positive $z$-axis, so we are in the $xy$-plane. With an angle of $\theta=\pi$, that puts us on the negative $x$-axis. The solution is $(x,y,z)=(-3,0,0)$.
- Draw the region in space described by $1\leq \rho \leq 3$, $0\leq \theta \leq \pi$, and $\pi/4\leq \phi\leq \pi/2$.
Solution
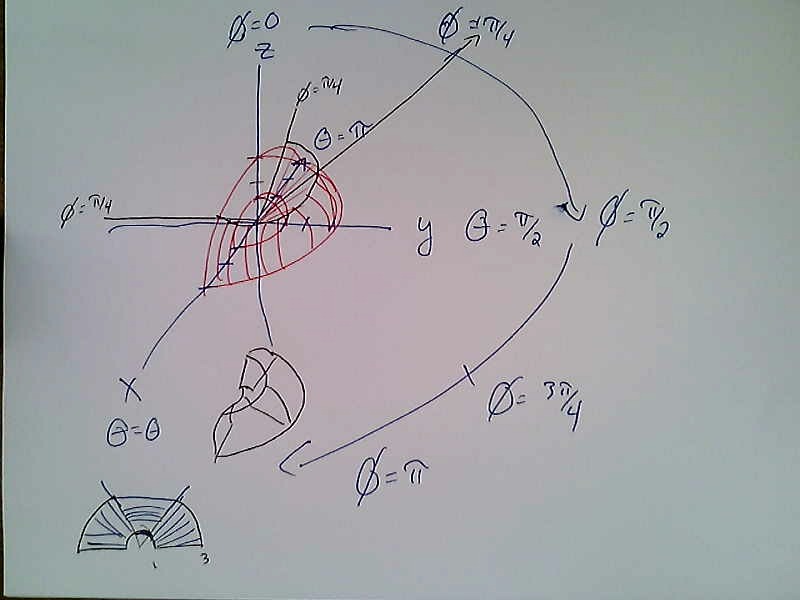
- Set up an integral formula to compute $\bar z$ for the solid above. (In spherical coordinates, the Jacobian is $\rho^2\sin\phi$ and we have $z=\rho\cos\phi$.)
Solution
We have $$\bar z = \frac{\int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{1}^{3}(\rho\cos\phi)(\rho^2\sin\phi) d\rho d\phi d\theta}{\int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{1}^{3}(\rho^2\sin\phi) d\rho d\phi d\theta}.$$
- A tennis ball has been cut in half. Suppose the inner radius of the tennis ball is 3 cm, and the outer radius is 3.5 cm. Give bounds of the form $?\leq \theta\leq ?$, $?\leq \phi\leq ?$, $?\leq \rho\leq ?$, to describe the bottom half ($z\leq 0$) of the tennis ball.
Solution
One option for the bounds is $0\leq \theta\leq 2\pi$, $\pi/2\leq \phi\leq \pi$, $3\leq \rho\leq 3.5$
- Consider the sphere $x^2+y^2+z^2=9$. Give a cylindrical equation for the sphere. Then give a spherical equation for the sphere.
Solution
In cylindrical, an equation is $r^2+z^2=9$. In spherical, an equation is $\rho = 3$.
Additional problems
- Set up an integral formula to compute each of the following:
- The average temperature of a metal plate in the $xy$-plane bounded by the curves $y=8-x^2$ and $y=x+2$, where the temperature at points on the plate is given by $f(x,y)=x+y^2$.

- The average charge density on a wire that lies along the helix $\vec r(t) = (3\cos t,3\sin t, 4t)$ for $0\leq t\leq 4\pi$, provided the charge at each point on the wire is given by $\sigma(x,y,z) = x^2+y^2+z$.

- The average pressure in a solid region in space inside the sphere $x^2+y^2+z^2=9$, provided the pressure at each point in the sphere is given by $p(x,y,z) = 10+x$.

- The spherical change-of-coordinates is given by $$(x,y,z) = (\rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, $(2,0,3\pi)$, and $(4,\pi/4,\pi/2)$.

- Give spherical coordinates $(\rho,\phi,\theta)$ for the Cartesian coordinates $(x,y,z)$ given by $(0,3,0)$, $(0,0,3)$, and $(1,2,2)$, $(3,0,4)$.

- Give an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates.

- Give an equation of the cone $x^2+y^2=z^2$ in spherical coordinates.

- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$.

- Give an equation of the plane $z=8$ in spherical coordinates.

- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$.

|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
