



Rapid Recall
Let $P=(3,0,0)$, $Q=(0,2,0)$, and $R=(0,0,1)$.
- Find a vector orthogonal to both $\vec {PQ}=\left<-3,2,0\right>$ and $\vec {PR}=\left<-3,0,1\right>$.
Solution
$$\left|\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\ -3 & 2& 0 \\ -3& 0 & 1\end{array} \right|=\left<2,3, 6\right>.$$
- Find the area of the triangle $\Delta PQR$.
Solution
We need half the area of the parallelogram formed from the vector above. We compute $$|\left<2,3, 6\right>| = \sqrt{4+9+36} = 7,$$ which means the area is 7/2.
- Suppose that $S=(x,y,z)$ is a point in the plane that passes through $P$, $Q$, and $R$, and note that $\vec {PS} = \left<x-3,y-0,z-0\right>.$ First compute $(\vec {PQ}\times \vec {PR})\cdot \vec {PS}$. Then explain why this dot product equals zero.
Solution
We have $$(\vec {PQ}\times \vec {PR})\cdot \vec {PS}=\left<2,3, 6\right>\cdot \left<x-3,y-0,z-0\right> = 2(x-3)+3(y-0)+6(z-0).$$ The dot product equals zero because $(\vec {PQ}\times \vec {PR})$ is orthogonal to any vector in the plane formed by $\vec {PQ}$ and $\vec {PR}$. This means an equation of the plane through $P$, $Q$, and $R$ is $$2(x-3)+3(y-0)+6(z-0)=0.$$
- Convert the integral $\int_0^{6\sqrt{2}/2} \int_{y}^{\sqrt{36-y^2}} x \, dx \, dy$ into polar coordinates.
Solution
A solution is $\int_{0}^{\pi/4} \int_0^{6} (r\cos\theta) \, r \, dr\,d\theta$.
- Draw the region in the first octant (all variables positive) that is bounded by the plane $\frac{x}{2}+\frac{y}{3}+\frac{z}{5}=1$. Then set up an integral to compute the volume of this region.
Solution
The region is a triangular pyramid. The plane passes through $(2,0,0)$, $(0,3,0)$, and $(0,0,5)$, so it is the region in space underneath this triangle. One integral (of 6 possible) that gives the volume is $$\int_{0}^{2}\int_{0}^{3(1-\frac{x}{2})}\int_{0}^{5(1-\frac{x}{2}-\frac{y}{3})}dzdydx.$$
Group problems
We did the first two as a class yesterday. I'd like you to redo them, and discuss any questions in your break out rooms. Before I set you loose though, let's graph the solid on the third bullet.
- Set up an integral formula to compute each of the following:
- The mass of a disc that lies inside the circle $x^2+y^2=9$ and has density function given by $\delta = x+10$
- The $x$-coordinate of the center of mass (so $\bar x$) of the disc above.
- The volume of the solid object in the first octant (all variables positive) that lies under the plane $2x+3y+6z=6$ (which we can also write as $\frac{x}{3}+\frac{y}{2}+\frac{z}{1}=1$.) Discuss this one for a minute, then expand the solution below.
Solution
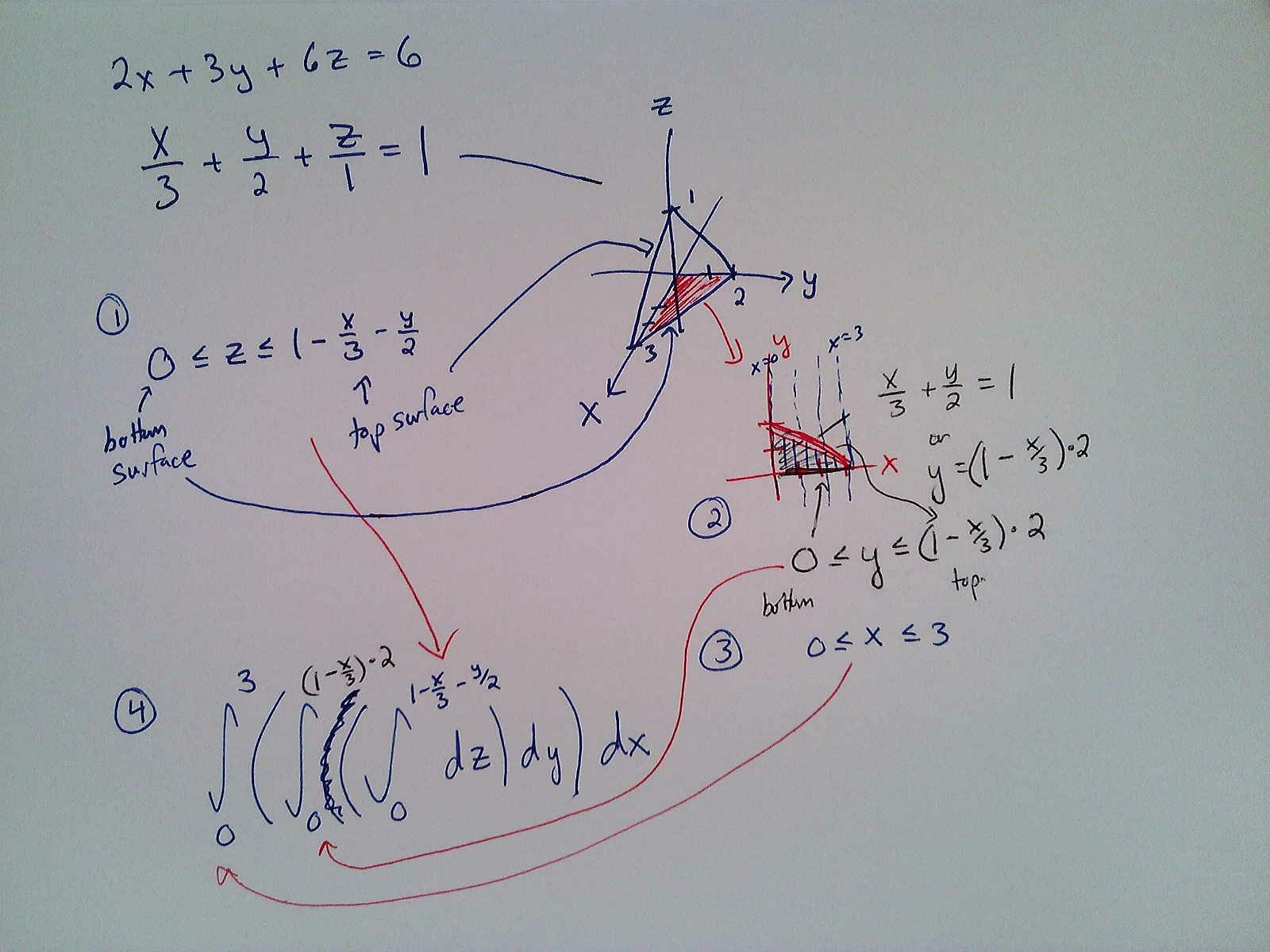
- Use the solution above to give a formula for the $y$-coordinate of the center-of-mass (so $\bar y$) of the same object (assume constant density).
- A wire lies along the curve $C$ parametrized by $\vec r(t) = (t^2+1, 3t, t^3)$ for $-1\leq t\leq 2$.
- Compute $ds$. (Remember - a little distance equals the product of the speed and a little time.)
- Set up integral formulas to find $\bar x$, then $\bar y$, then $\bar z$, for the centroid of $C$.
- Consider $\int_{0}^{4}\int_{x}^{4}\cos(y^2)dydx$.
- Draw the region described by the bounds.
- Swap the order of the bounds on the integral (use $dxdy$ instead of $dydx$).
- Actually compute the integral.
- Draw the region described the bounds of each integral. (Use the Mathematica notebook Integration.nb to check your work.)
- $\ds\int_{0}^{3}\int_{0}^{9-x^2}\int_{0}^{3-x}dzdydx$
- $\ds\int_{0}^{1}\int_{0}^{1-z}\int_{0}^{\sqrt{1-x^2}}dydxdz$
- $\ds\int_{0}^{3}\int_{0}^{\pi}\int_{0}^{5}rdzdrd\theta$
- $\ds\int_{-1}^{1}\int_{0}^{1-y^2}\int_{0}^{x}dzdxdy$
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
