



Rapid Recall
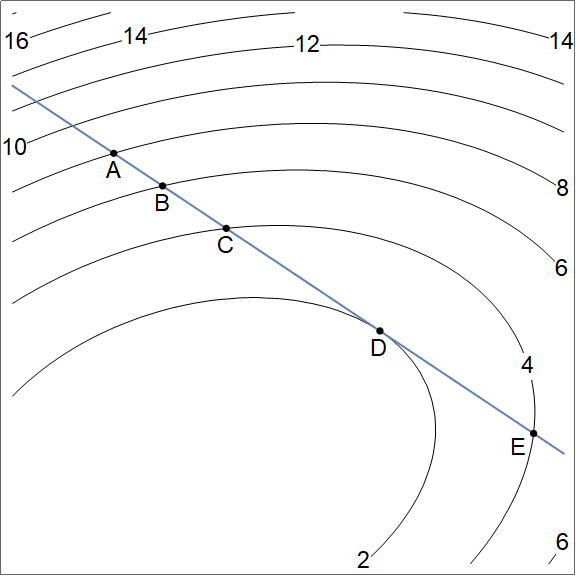
Use the figure above to order or compute the directional derivatives as requested.
- List the following in decreasing order: $D_{\vec {BC}}f(A)$, $D_{\vec {BC}}f(B)$, $D_{\vec {BC}}f(C)$, $D_{\vec {BC}}f(D)$, $D_{\vec {BC}}f(E)$.
Solution
Notice that the direction $\vec{BC}$ is the same for each directional derivative. So all we really need to do is compare the slopes in the "south-east" direction at each of the 5 points. Because the contours have labels on them, we see that moving from $A$ to $B$ results in drop, so a negative slope. This is true at $A$, $B$, and $C$. Because the distance to level curves increases as we move south east starting at $A$, we can tell that the slope is most negative at $A$. At $D$ the slope is zero in the $\vec{BC}$ direction, and at $E$ the slop is positive. Ordering them in decreasing order then gives $$D_{\vec {BC}}f(E) > D_{\vec {BC}}f(D) > D_{\vec {BC}}f(C) > D_{\vec {BC}}f(B) > D_{\vec {BC}}f(A).$$
- Evaluate $D_{\vec {BC}}f(D)$.
Solution
At point $D$, when moving in the southeast direction, we hit a local minimum. As such, the slope here is definitely zero in the $\vec{BC}$ direction. The fact that the path the rover is on is tangent to the level curve here is also a great reason as to why this slope is zero.
- List the following in decreasing order: $D_{\vec {AB}}f(B)$, $D_{\vec {BC}}f(B)$, $D_{\vec {CD}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
Notice that the point $B$ is the exact same in each of these. Also notice that $\vec {AB}$, $\vec {CD}$, and $\vec{DE}$ all point in the same southeast direction. As such, these quantities are all equal. The direction is the same, and the point is the same, so the requested slopes are equal. This gives $$D_{\vec {AB}}f(B) = D_{\vec {BC}}f(B) = D_{\vec {CD}}f(B) = D_{\vec {DE}}f(B).$$
- List the following in decreasing order: $D_{\vec {DC}}f(B)$, $D_{\vec {DE}}f(B)$.
Solution
The direction $\vec {DC}$ is northwest, while the direction $\vec{DE}$ is southeast. Standing at point $B$, moving southeast results in a drop in height while moving northwest results in an increase in height. As such, we have $$D_{\vec {DC}}f(B) > D_{\vec {DE}}f(B).$$ We can actually say more in this problem Because the point is the same, and the directions are opposite, we know they are equal and opposite, giving us $$D_{\vec {DC}}f(B) = - D_{\vec {DE}}f(B).$$
- Suppose a plane passes through the point $(a,b,c)$ and has normal vector $(A,B,C)$. Give an equation of that plane.
Solution
If $Q = (x,y,z)$ is any other point on the plane, then $\vec {PQ} = (x-a,y-b,z-c)$ is a vector in the plane. Since $\vec n = (A,B,C)$ is normal to the plane, then we know $\vec n$ and $\vec {PQ}$ are orthogonal, which means $\vec n\cdot \vec {PQ}=0$. This gives an equation of the plane as $$(A,B,C)\cdot (x-a,y-b,z-c)=0\quad\text{or}\quad A(x-a)+B(y-b)+C(z-c)=0.$$
Group problems
- Give an equation of the tangent plane to $f(x,y)=x^2+4xy+3y^2$ at the point $(2,1)$.
Solution
Differentials give $df = (2x+4y)dx+(4x+6y)dy$. Our point is $x=2$ and $y=1$, so we have $dx=x-2$ and $dy=y-1$. Substitution into the original function gives $f(2,1) = 15$ and so $df = z-15$. Substitution into the differential gives $$ \underbrace{z-15}_{dz} = \underbrace{(2(2)+4(1))}_{f_x(2,1)}\underbrace{(x-2)}_{dx}+\underbrace{(4(2)+6(1))}_{f_y(2,1)}\underbrace{(y-1)}_{dy} \quad \text{or} \quad z-15 = 8(x-2)+14(y-1) .$$
- For the function $f(x,y)=x^2+4xy+3y^2$, compute the first derivative $Df(x,y)$ and the second derivative $D^2f(x,y)$. Hint: Recall that, for a scalar function $f(x,y)$, the derivative is the same as the gradient, i.e., $Df(x,y)=\vec\nabla f(x,y)$, a $1\times2$ matrix. The second derivative $D^2f(x,y)$ will be a $2\times2$ matrix.
Solution
Remember that the derivative is a matrix. We can write the differential $df = (2x+4y)dx+(4x+6y)dy$ as the product of a matrix and a vector using $df = \begin{bmatrix}2x+4y&4x+6y\end{bmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}$. This gives $$Df(x,y) = \begin{bmatrix}2x+4y&4x+6y\end{bmatrix}.$$ The differential of the first derivative is $$dDf(x,y) = \begin{pmatrix}2\\4\end{pmatrix}dx+ \begin{pmatrix}4\\6\end{pmatrix}dy =\begin{bmatrix}\begin{pmatrix}2\\4\end{pmatrix}&\begin{pmatrix}4\\6\end{pmatrix}\end{bmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}. $$ This gives $$D^2f(x,y) = \begin{bmatrix}\begin{matrix}2\\4\end{matrix}&\begin{matrix}4\\6\end{matrix}\end{bmatrix}.$$
- A rover travels along the path $2x-4y=12$. The elevation is given by $z=x+y^2-3$. Find the $(x,y)$ location of the lowest elevation reached by the rover along this path.
Solution
We have $f(x,y) = x+y^2-3$, $g(x,y)=2x-4y$, and $c=12$. Gradients are $\vec \nabla f = (1,2y)$ and $\vec \nabla g = (2,-4)$. The system $\vec \nabla f = \lambda \vec \nabla g$, along with $g=c$ gives the equations $$1=\lambda 2,\quad 2y=\lambda (-4),\quad 2x-4y=12.$$ The solution is $\lambda = 1/2$, $y=-1$, and $x=4$. The requested location is $(x,y)=(4,-1)$.
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$.
Solution
Computing the differential of both sides of the original equation gives $ydx+xdy+2zdz=0$. Substituting $x=-3$, $y=-2$, $z=1$, $dx=x-(-3)$, $dy = y-(-2)$, and $dz = z-1$ into the differential gives the tangent plane equation as $$(-2)(x-(-3))+(-3)(y-(-2))+2(1)(z-1)=0 .$$
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$.
Solution
Computing the differential of both sides of the original equation gives $dz=y^2dx+2xydy$. Substituting $x=4$, $y=-1$, $z=4(-1)^2=4$, $dx=x-(4)$, $dy = y-(-1)$, and $dz = z-4$ into the differential gives the tangent plane equation as $$z-4 = (-1)^2(x-4)+2(4)(-1)(y-(-1)) .$$
Presenters
- Kyle
- Tyler
- ??? (volunteer)
- William
- ??? (volunteer)
The 5 above is more than sufficient for today. If someone completed 33, and there is time, feel free to discuss that one today.
- (Mathematica)
- (Mathematica)
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
