



I'll be in Provo Utah, dropping my daughter off at the MTC (she's headed to New Zealand). Today in class, we'll have 3 people present their work, and then let you spend the rest of the hour working on problems. Please use the Mathematica notebook Integration.nb to have software plot your guess for the bounds (this will let your rapidly check if you did something right).
Rapid Recall
- Consider the region $R$ in the plane that lies below $y = f(x)$ and above $y=g(x)$, for $a\leq x\leq b$. Set up formulas involving iterated double integrals to compute both $\bar x$ and $\bar y$.
Solution
The centroid is $$\bar x = \frac{\int_a^b\int_{g(x)}^{f(x)}x dy dx}{\int_a^b\int_{g(x)}^{f(x)} dy dx} \quad\text{and}\quad \bar y = \frac{\int_a^b\int_{g(x)}^{f(x)}y dy dx}{\int_a^b\int_{g(x)}^{f(x)} dy dx}.$$ Note that if we had a density function $\delta (x,y)$, then the center-of-mass would be $$\bar x = \frac{\int_a^b\int_{g(x)}^{f(x)}x \delta(x,y) dy dx}{\int_a^b\int_{g(x)}^{f(x)} \delta(x,y)dy dx} \quad\text{and}\quad \bar y = \frac{\int_a^b\int_{g(x)}^{f(x)}y \delta(x,y) dy dx}{\int_a^b\int_{g(x)}^{f(x)} \delta(x,y) dy dx}.$$
- Draw the solid whose volume is given by the integral $\ds\int_{0}^{\pi}\int_{\pi/3}^{\pi/2}\int_{0}^{3}\rho^2\sin\phi \,d\rho \,d\phi \,d\theta$.
Solution
This image was created using the Mathematica notebook Integration.nb.
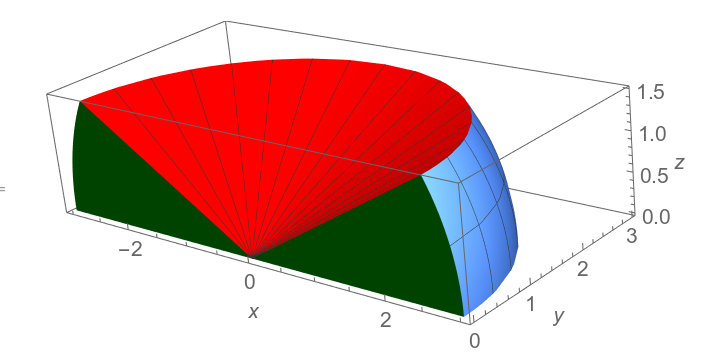
- Set up an integral formula to compute the $z$-coordinate of the center of mass of the solid above, provided the density is given by $\delta = x^2+y^2+z^2$.
Solution
The bounds don't change at all, rather we just have to add the correct pieces from the center-of-mass formulas. Note that $z=\rho\cos\phi$ and $\delta = \rho^2$. $$\bar z = \frac{\iiint_Dz\delta dV}{\iiint_D\delta dV}=\frac{\ds\int_{0}^{\pi}\int_{\pi/3}^{\pi/2}\int_{0}^{3}(\rho \cos\phi)(\rho^2) \rho^2\sin\phi d\rho d\phi d\theta}{\ds\int_{0}^{\pi}\int_{\pi/3}^{\pi/2}\int_{0}^{3}(\rho^2) \rho^2\sin\phi d\rho d\phi d\theta}$$
- The temperature at points in the solid above is given by $T(x,y,z) = x+2y$. Set up an integral that would find the average temperature in the solid.
Solution
This is almost exactly the same as above. There is no density, and instead of finding the average $z$ value, we now want the average $T$ value. So just swap out $z$ for $T$ and we get $$\bar T = \frac{\iiint_D T dV}{\iiint_D dV}=\frac{\ds\int_{0}^{\pi}\int_{\pi/3}^{\pi/2}\int_{0}^{3}(\rho\sin\phi\cos\theta+2\rho\sin\phi\sin\theta) \rho^2\sin\phi d\rho d\phi d\theta}{\ds\int_{0}^{\pi}\int_{\pi/3}^{\pi/2}\int_{0}^{3} \rho^2\sin\phi d\rho d\phi d\theta}$$
Presentations
- 38 - Sabrina
- 39 - Jesse
- 36 - A volunteer who passed yesterday - or Alan can finish it (the cylindrical integral).
Group problems
- (Spherical Coordinates) The spherical change-of-coordinates is given by $$(x,y,z) = (\rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi).$$
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. Remember that the Jacobian for spherical coordinates is $|\rho^2\sin\phi|$.
- Use the Mathematica notebook Integration.nb to draw the region described your bounds in the previous problem. Update your bounds if you find any errors.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8/\cos\phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$. Check your answer with software.
- (Cylindrical Coordinates - Disc and Shell method) This sequence of problems has you work with one solid in several different ways. It also has you develop the disc and shell method as by-products of cylindrical coordinates, where the only difference is the order of integration.
- Draw the solid region in space that is bounded above by $z=9-x^2-y^2$ (so $z=9-r^2$) and below by the $xy$-plane.
- Set up a triple integral in Cartesian coordinates to compute the volume of this solid. Use software to check your answer.
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta drdz$. Check with software.
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{9} \pi (\sqrt{9-z})^2 dz$. Recall the disc-method $$V = \int dV =\int_a^b \underbrace{\pi (\text{rad of disc at $z$})^2}_{\text{area of disc at height $z$}} \underbrace{dz}_{\text{little height}}.$$
- Set up a triple integral in cylindrical coordinates to compute the volume of this solid using the order $d\theta dzdr$. Check with software.
- Compute the two inside integrals and simplify to show that $V = \int_{0}^{3} 2\pi r (9-r^2) dr$. Recall the shell-method $$V = \int dV = \int_a^b \underbrace{(2\pi r)(\text{height of shell at $r$})}_{\text{shell surface area = (circumference)(height)}} \underbrace{dr}_{\text{shell thickness}}.$$
- Use any remaining time to pick some problems from the list below, and tackle them.
Textbook practice
If you want more integrals to work with. These all come from Thomas's calculus, the 14th edition. Feel free to tackle these in your group today in class, if you have extra time.
- Double integrals - Swapping order - 15.2: 33-54
- Polar integrals - 15.4: 1-8, 9-22 (swap to polar and then use software to check)
- Triple integrals - 15.5: 21-36
- Cylindrical and Spherical- 15.7: 37-42 (cyl), 55-60 (sph), 65-84 (BEST ones, you have to pick the system, draw the region, set things up - use the Mathematica notebook Integration.nb to check if your bounds are right).
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
