Task 42.1
Imagine that the vector field $\vec F(x,y,z)$ represents the velocity of some fluid at point $(x,y,z)$. Let $S$ be a surface (you could think of water flowing through a fish net) through which the fluid will flow. The flux of $\vec F$ across $S$ is the rate at which the fluid flows through the surface.


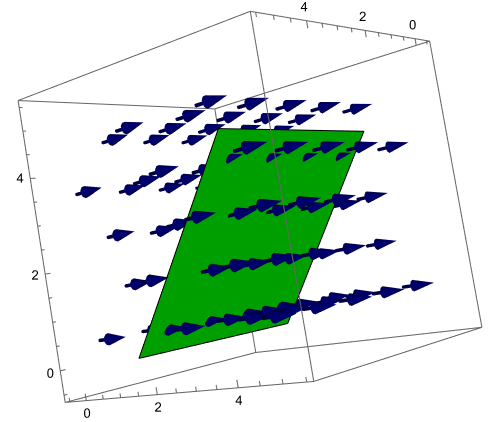
- In the pictures above, the velocity is given by $\vec F = (0,2,0)$ meters per second and the green surface $S$ is a square with surface area 25 square meters. For each picture above, let's determine the flux of $\vec F$ across $S$.
- Explain why the flow rate of $\vec F$ through $S$ for the first image above is 50 cubic meters per second.
- Explain why the flow rate of $\vec F$ through $S$ for the second image above is 0 cubic meters per second.
- In the third image, the edges of the parallelogram are given by $\vec u = (5,0,0)$ and $\vec v = (0,3,4)$. Compute the flow rate of $\vec F$ through $S$.
In our computations above, we were not concerned about which direction the fluid flowed through the surface. In general, we'll keep track of which direction a fluid flows through a surface, and count flux as negative when the fluid flows the opposite direction. To do this, we pick a unit vector $\hat n$ to the surface, called an orientation of $S$, and decide flux is positive precisely when the vector component of $\vec F$ that is parallel to $\hat n$ is in the same direction as $\hat n$.
- In the third image above, a normal vector to the surface is $\vec u\times \vec v = (5,0,0)\times (0,3,4) = (0,20,-15)$, which means we can use $\hat n = \frac{\vec u\times \vec v}{|\vec u\times \vec v|} = \frac{1}{5}(0,4,-3)$ as an orientation for $S$. Show that the flux of $\vec F$ across $S$ with the orientation $\hat n$ is $ ( \vec F\cdot \hat n)( \text{Surface Area of $S$ } )$.
The computations above generalize rapidly to provide a method for computing the flux of a vector field $\vec F$ across a surface $S$ in the direction of $\hat n$. For a vector field $\vec F$ and surface $S$ with orientation $\hat n$, we have used $dS$ to represent small bits of surface area. This means a small amount of flux across $S$ is given by $d\text{Flux} = \vec F\cdot \hat n dS$. Summing these, and computing a limit provides the flux as $$\text{Flux}=\Phi = \iint_S \vec F\cdot \hat n dS.$$ Note that because $\hat n$ is a unit normal vector to $S$, then given a parametrization $\vec r(u,v)$ of $S$ for $(u,v)$ in some region $R$, we know $\hat n = \pm \frac{\vec r_u\times \vec r_v}{|\vec r_u\times \vec r_v|} $ while $dS = |\vec r_u\times \vec r_v|dudv$. This means we can simplify the flux integral above to $$\text{Flux}=\Phi = \iint_R \vec F \cdot (\pm\vec r_u\times \vec r_v)dudv,$$ where the $\pm$ sign must be determined based on the orientation of the surface.
- Let $\vec F = (x^2 + y, y - z, 3 x + 2 z)$ and $S$ be the surface parametrized by $\vec r(u,v) = (3 \cos v,u,3\sin v)$ for $1\leq u\leq 5$ and $0\leq v\leq 2\pi$. Let $\hat n$ be the unit normal to $S$ which points outwards, away from the $y$-axis. Compute the outward flux $\Phi$ of $\vec F$ across $S$. The steps below can serve as a guide.
- Compute $\vec r_u$ and $\vec r_v$.
- Compute a normal vector $\vec N = \vec r_u \times \vec r_v$, and decide if $\vec N$ points in the same, or opposite direction, as the orientation $\hat n$. This may require you to draw the surface to visually make that determination.
- Insert all the known values into $\iint_R \vec F\cdot (\pm\vec r_u\times \vec r_v)dudv$, making sure all variables have been written in terms of $u$ and $v$. Then use software to compute the integral. (I got $72\pi$.)
- Let $\vec F = (2 y z, x + 3 y, -z^2)$ and $S$ be the surface parametrized by $\vec r(u,v) = (u \cos v, u \sin v, 9 - u^2)$ for $0\leq u\leq 3$ and $0\leq v\leq 2\pi$. Compute the upward ($\hat n$ has positive $z$-component) flux $\Phi$ of $\vec F$ across $S$ in the direction of $\hat n$. The steps above are still the same guide. (I got $-243\pi/2$.)
Task 42.2
For a surface $S$ with parametrization $\vec r(u,v) = (x(u,v),y(u,v),z(u,v))$ for $(u,v)$ in some region $R$, we have shown that surface area is $$S = \iint_S dS = \iint_R |\vec r_u\times\vec r_v|dudv.$$ This means we can compute mass, average values, centroids, centers-of-mass, etc, in a manner similar to what we have already done.
- For a function $f$ defined at points on the surface, the average value is $$\bar f = \frac{\iint_S f dS}{\iint_S dS} = \frac{\iint_R f(u,v) |\vec r_u\times\vec r_v| dudv}{\iint_R |\vec r_u\times\vec r_v| dudv}.$$ Replacing $f$ with $x$, $y$, or $z$ obtains the corresponding coordinate of the centroid of the surface.
- Given a density $\delta$ at points on the surface, the mass of the surface is $$ m = \iint_S dm = \iint_S \delta dS = \iint_R \delta(u,v) |\vec r_u\times\vec r_v| dudv.$$ The center-of-mass is given by $(\bar x, \bar y, \bar z) = \frac{\iint_S (x,y,z) \delta dS}{\iint_S \delta dS}$ which we can write as $$\begin{align*} \bar x &= \frac{\iint_R x(u,v) \delta(u,v) |\vec r_u\times\vec r_v| dudv}{\iint_R \delta(u,v) |\vec r_u\times\vec r_v| dudv},\\ \bar y &= \frac{\iint_R y(u,v) \delta(u,v) |\vec r_u\times\vec r_v| dudv}{\iint_R \delta(u,v) |\vec r_u\times\vec r_v| dudv},\\ \bar z &= \frac{\iint_R z(u,v) \delta(u,v) |\vec r_u\times\vec r_v| dudv}{\iint_R \delta(u,v) |\vec r_u\times\vec r_v| dudv}. \end{align*}$$
Note that there are lots of things going on with each integral. Software will greatly reduce the amount of time needed to set up and compute these integrals. The commands that will be most useful are ParametricPlot3D[], D[], Cross[], Norm[], and Integrate[].
- Consider the surface $\vec r(u,v) = (3\cos v,3\sin v, u)$ for $1\leq u\leq 5$ and $0\leq v\leq \pi$. Start by drawing the surface. From your picture, state $\bar x$ and $\bar z$. Then set up and compute an integral formula that gives the $y$-coordinate of the centroid.
- A satellite dish lies along the parametric surface $\vec r(u,v) = (u^2, u\cos v, u\sin v)$ for $0\leq u\leq 2$ and $0\leq v\leq 2\pi$. Start by drawing the surface. The temperature at points on and near the dish is given by $T(x,y,z) = x+z$. Set up and compute an integral formula that gives the average temperature of the satellite dish.
- The top half of the surface $S$ of a donut (a torus) can be parametrized by $\vec r(u,v) = ((5 - 3 \cos u) \cos v, (5 - 3 \cos u) \sin v, 3 \sin u)$ for $0\leq u\leq \pi$ and $0\leq v\leq 2\pi$. Imagine that someone puts icing on the top of this donut (so creates a surface), but the thickness of the icing is more on the top of the donut than on the sides. While not a perfect way to model this situation, we could use $\delta = kz$ for some constant $k$ as a way to model the surface with varying density. Show that the center-of-mass of the surface $S$ with density function $\delta = kz$ is $(\bar x, \bar y, \bar z) = (0,0,\frac{3\pi}{4})$.
Task 42.3
We've seen all the new notation that we'll encounter for the rest of the semester. This task has us practice using the notation we've learned.
- Consider the vector field $\vec F = (x,x-z,y+z)$, the surface $S$ parametrized by $\vec r(u,v)=(u^2, u\cos v, u\sin v)$ for $0\leq u\leq 2$ and $0\leq v\leq 2\pi$, and the curve $C$ parametrized by $\vec r(t) = (4,2\cos t, 2\sin t)$ for $0\leq t\leq 2\pi$.
- Draw the surface $S$ and curve $C$. How are these two objects related?
- Compute $\vec N = \vec r_u\times \vec r_v$ and determine if $\vec N$ points inward toward the $x$-axis, or outwards away from the $x$-axis.
- Set up and compute the integral $\ds \int_C Mdx+Ndy+Pdz$, computing the work done by $\vec F$ along $C$.
- Set up and compute $\ds \iint_S \vec \nabla \times \vec F\cdot \hat n dS$, computing the flux of the curl of $\vec F$ across $S$ in the direction $\hat n$ outwards away from the $y$-axis.
- Consider the vector field $\vec F = (x,x-z,y+z)$, the solid domain $D$ that lies inside the sphere $x^2+y^2+z^2=25$, and the surface $S$ parametrized by $\vec r(u,v)=(5\sin v\cos u, 5 \sin v \sin u, 5 \cos v)$ for $0\leq u\leq 2\pi$ and $0\leq v\leq \pi$.
- Draw the surface $S$ and domain $D$. How are these two objects related?
- Compute $\vec N = \vec r_u\times \vec r_v$ and determine if $\vec N$ points inward toward the domain $D$ or outwards away from the domain $D$.
- Set up and compute $\ds \iint_S \vec F\cdot \hat n dS$ for $\hat n$ pointing outwards, away from the solid inside $S$. This computes the outward flux of $\vec F$ across $S$.
- Set up and compute $\ds \iiint_D \vec \nabla \cdot \vec F dV$, the triple integral of the divergence of $\vec F$ over the domain $D$.
Task 42.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
