Day 34

Task 34.1

It's time to focus on how area is changed when we perform a change-of-coordinates. We'll see that finding the area of a transformed parallelogram is the key.

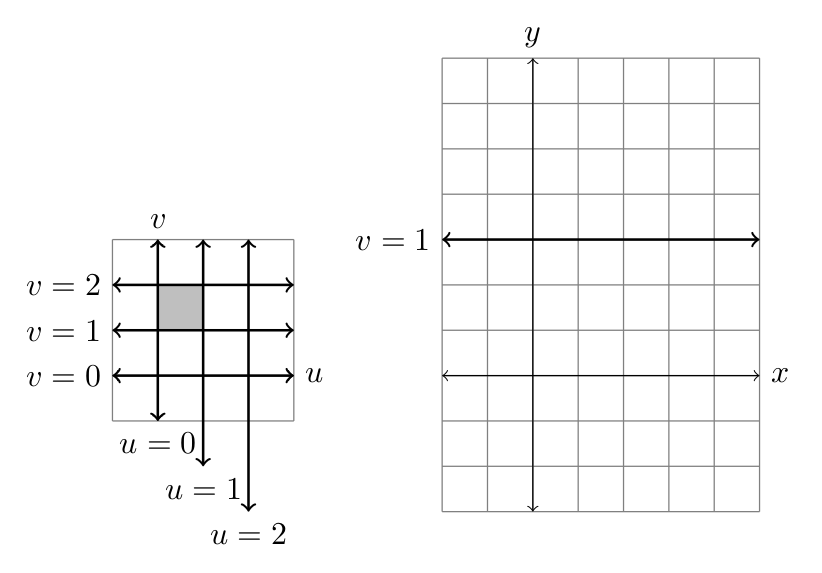
1. Consider the change-of-coordinates $x=2u$, $y=3v$.
   1. The lines $u=0,u=1,u=2$ and $v=0,v=1,v=2$ correspond to lines in the $xy$-plane. Draw these lines in the $xy$-plane (the line $v=1$ is done for you).
      • 
   2. The box in the $uv$-plane with $0\leq u\leq 1$ and $1\leq v\leq 2$ corresponds to a box in the $xy$-plane. Shade this box in the $xy$-plane and find its area.
   3. Compute the differentials $dx$ and $dy$. State them using the vector form (linear combination) $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix} ?\\ ?\end{pmatrix}du+\begin{pmatrix}?\\?\end{pmatrix}dv$$ What do the two vectors $(a,0)$ and $(0,b)$ have to do with your picture?
   4. Draw the box given by $-1\leq u\leq 1$ and $-1\leq v\leq 1$ in both the $uv$-plane and $xy$-plane. Then state the area $A_{uv}$ of this box in the $uv$-plane, and state the area $A_{xy}$ of the corresponding rectangle in the $xy$-plane.
   5. Consider the circle $u^2+v^2=1$, whose area inside is $A_{uv}=\pi$. Guess the area $A_{xy}$ inside the corresponding ellipse in the $xy$-plane. Explain.
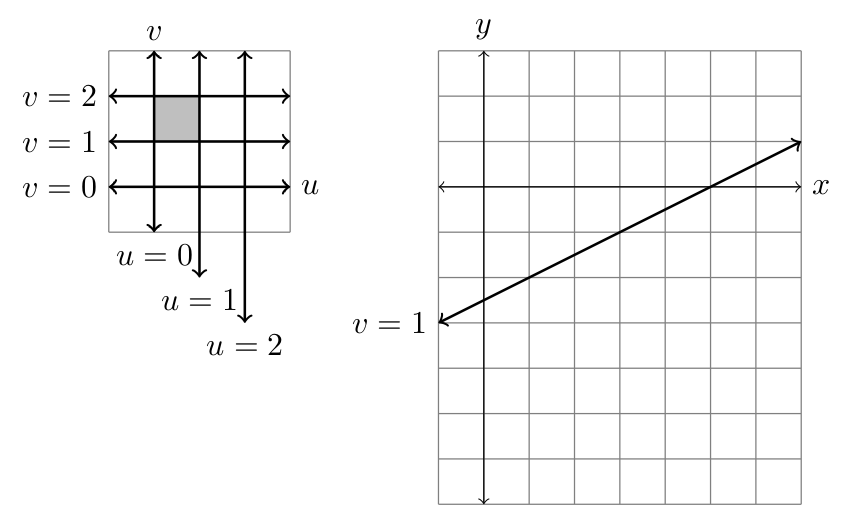
2. Consider now the change-of-coordinates $x=2u+v$, $y=u-2v$.
   1. The lines $u=0,u=1,u=2$ and $v=0,v=1,v=2$ correspond to lines in the $xy$ plane. Draw these lines in the $xy$-plane (the line $v=1$ is drawn for you). One option is to find the $xy$ coordinates of the $(u,v)$ points $(0,0)$, $(0,1)$, $(0,2)$, $(1,0)$, $(1,1)$, etc., and then just connect the dots to make a rotated grid.
      • 
   2. The box in the $uv$-plane with $0\leq u\leq 1$ and $1\leq v\leq 2$ should correspond to a parallelogram in the $xy$ plane. Shade this parallelogram in your picture above.
   3. Compute the differentials $dx$ and $dy$. State them using the vector form (linear combination) $$\begin{pmatrix}dx\\dy\end{pmatrix} = \begin{pmatrix} ?\\ ?\end{pmatrix}du+\begin{pmatrix}?\\?\end{pmatrix}dv.$$ What do the two vectors above have to do with your picture?
   4. Show that the area of the parallelogram formed using these two vectors is 5. How would you describe the change in area between the graph in the $uv$-plane, and the graph in the $xy$-plane?

The following code will help you check that your work on the second part is correct.

coordinates = {2 u + v, u - 2 v}
R = ParametricRegion[{coordinates, 0 <= u <= 1 && 1 <= v <= 2}, {u, v}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]
R = ParametricRegion[{coordinates, u == 0 || u == 1 || u == 2 || v == 0 || v == 1 || v == 2}, {{u, -1, 3}, {v, -1, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]

Task 34.2

Many vector fields are the derivative of a function. This function we call a potential for the vector field. Once we are comfortable finding potentials, we'll show that the work done by a vector field with a potential is the difference in the potential.

Let's practice finding gradients and potentials. You're welcome to watch this YouTube Video before starting, or just jump in and give it a try.

1. Let $f(x,y) = x^2+3xy+2y^2$. Find $\vec \nabla f$. Then compute $D^2f(x,y)$ (you should get a square matrix). What are $f_{xy}$ and $f_{yx}$?
2. Consider the vector field $\vec F(x,y)=(2x+y,x+4y)$. Find the derivative of $\vec F(x,y)$ (it should be a square matrix). Then find a function $f(x,y)$ whose gradient is $\vec F$ (i.e. $Df=\vec F$). What are $f_{xy}$ and $f_{yx}$?
3. Consider the vector field $\vec F(x,y)=(2x+y,3x+4y)$. Find the derivative of $\vec F$. Why is there no function $f(x,y)$ so that $Df(x,y)=\vec F(x,y)$? [Hint: look at $f_{xy}$ and $f_{yx}$.]

4. For each of the following vector fields, start by computing the derivative. Then find a potential, or explain why none exists.
   1. $\vec F(x,y)=(2x-y, 3x+2y)$
   2. $\vec F(x,y)=(2x+4y, 4x+3y)$
   3. $\vec F(x,y)=(2x+4xy, 2x^2+y)$
   4. $\vec F(x,y,z)=(x+2y+3z,2x+3y+4z,2x+3y+4z)$
   5. $\vec F(x,y,z)=(x+2y+3z,2x+3y+4z,3x+4y+5z)$
   6. $\vec F(x,y,z)=(x+yz,xz+z,xy+y)$

The Mathematica code below starts by computing the derivative $D\vec F$, then uses DSolve to find a potential, and finishes by computing the gradient of the potential to see if it is the original vector field (verify you have the correct solution). If a potential exists, then the last line should match the first. You'll need to add a third variable (,z) in appropriate spots to use this code for a 3D vector field.

ClearAll[F, f, x, y]
F = {2 x + y, x + 4 y}
D[F, {{x, y}}] // MatrixForm
potential = DSolve[D[f[x, y], {{x, y}}] == F, f[x, y], {x, y}]
D[f[x, y] /. potential, {{x, y}}] // Flatten

Task 34.3

We already found the area of parallelogram in the $xy$-plane. To use new coordinate systems in 3D, we'll need to volume of a parallelepiped formed by the three vectors $\vec u$, $\vec v$, and $\vec w$, shown in the image below.

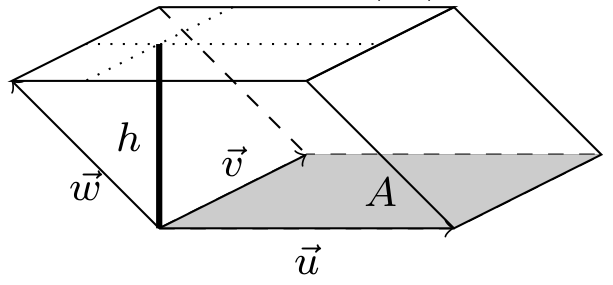
We get the volume by obtaining the area $A$ of one face, multiplied by the distance $h$ between the base and the plane containing the opposing face. This means we need to (1) compute the area of a parallelogram in 3D, and then (2) obtain a formula for the distance between the opposing faces. In this task, we'll see that the cross product and dot product provide us with precisely the tools we need to do both tasks.

1. Let $\vec u = (a,b,c)$ and $\vec v = (d,e,f)$. Our goal is to find the area of a parallelogram whose edges are formed from these two vectors.
   1. Draw a picture that contains 2 vectors labeled $\vec u$ and $\vec v$. In that picture, include $\vec u_{\parallel \vec v}$ and $\vec u_{\perp\vec v}$. Explain why the area we seek is $A = |\vec u_{\perp\vec v}||\vec v|$. Then use the following Mathematica code to compute the area. The Assumptions command below is needed to help Mathematica do some simplifications .

      $Assumptions = a \[Element] Reals && b \[Element] Reals && c \[Element] Reals && d \[Element] Reals && e \[Element] Reals && f \[Element] Reals;
      u = {a, b, c};
      v = {d, e, f};
      uPerpv = u - Projection[u, v];
      Norm[uPerpv]*Norm[v] // Simplify
      

   2. The magnitude of the cross product is $$|\vec u\times \vec v|= |(bf-ce, cd-af, ae-bd)| = \sqrt{(bf-ce)^2+ (cd-af)^2+ (ae-bd)^2}.$$ Show that the magnitude of the cross product and the area of the parallelogram (the value you obtained above) are the same. You can do this by hand, or with Mathematica. If you choose to use Mathematica, here is code for getting the magnitude of the cross product.

      Norm[Cross[u, v]] // Simplify
      

   3. Use what you just learned to find the area of the parallelogram formed by the two vectors $(1,2,3)$ and $(-3,1,4)$.

Now that we have a formula for the area of one face of a parallelepiped, we only need to find the distance between opposing faces to obtain the volume.

2. Consider three vectors $\vec u$, $\vec v$, and $\vec w$ in $\mathbb{R}^3$. We will find the volume of the parallelepiped formed by these three vectors. Let the base of the parallelogram be the face formed by $\vec u$ and $\vec v$. The height $h$ is the distance between the plane that contains the base and the plane that contain the opposing side of the parallelepiped.
   1. Give a formula to compute the area of the base of the parallelogram. (What did the first part of this tasks help us learn)
   2. Give a vector $\vec n$ that is normal to the base.
   3. Use the projection formula, with the vectors $\vec w$ and $\vec n$ in an appropriate manner, to state the height $h$ of the parallelogram in terms of dot products.
   4. Use your work above to explain why the parallelepiped's volume is $$V=|(\vec u\times \vec v)\cdot \vec w|.$$

Task 34.4

Pick some problems related to the topics we are discussing from the Text Book Practice page.