Task 27.1
We can think of any object (such as a rover) as consisting of many little parts. Each little part contributes a little mass $dm$ and a center-of-mass. We can predict these quantities prior to building the rover, before we can weigh anything. We just need the length $ds$, area $dA$, or volume $dV$ of a small part, together with the material's density $\delta$ (mass per length, area, or volume, as appropriate).
- For thin wires, we get little masses $dm$ by multiplying little lengths $ds$ by a density $\delta$ with units of mass per length.
- For thin plates, we get little masses $dm$ by multiplying little areas $dA$ by a density $\delta$ with units of mass per area.
- For solid objects, we get little masses $dm$ by multiplying little volumes $dV$ by a density $\delta$ with units of mass per volume.
In all three cases, we can obtain the total mass $m$ by adding up the little masses with an integral. The difference between the three cases will be whether we use a single, double, or triple integral. Often the density $\delta$ will be constant throughout an entire object. However, composite materials exist where density $\delta (x,y,z)$ can vary throughout an object. We can then compute the center-of-mass using the average value formula.
Consider a thin rod (like a drive shaft or thinner) that lies along the $z$-axis for $a\leq z\leq b$.
- Suppose first that the rod is made out of a single material whose density is given by the constant $\delta$ g/m (mass per length).
- A small part of the rod has length $dz$. Compute $\int_a^b dz$, and explain what physical quantity this integral computes.
- A small bit of the rod has mass $dm = \delta dz$. Compute the total mass by computing $\int_a^b \delta dz$. Remember that $\delta$ is a constant.
- Guess the location of the average $z$-value of the rod (the center-of-mass).
- To validate your guess, compute and simplify the average value integral formula $$\bar z = \frac{\ds\int_a^b z dm}{\ds\int_a^b dm} = \frac{\ds\int_a^b z \delta dz}{\ds\int_a^b \delta dz}.$$
- Now suppose the rod is more like an antenna and the rod gets thinner as we move up the rod. This means the density $\delta(z)$ is now a function of $z$. Let's use, for simplicity, the linear density function $\delta(z)=b-z$.
- What is the density of the rod at $a$? What is the density of the rod at $b$? Construct a rough sketch of a rod that could have this type of density function.
- A small bit of the rod has mass $dm = \delta(z) dz$. Compute the total mass by computing $\int_a^b \delta(z) dz = \int_a^b (b-z)dz$.
- Is the location of $\bar z$ closer to $z=a$ or $z=b$? Explain.
- Find the $z$-coordinate of the center-of-mass by computing $$\bar z = \frac{\ds\int_a^b z dm}{\ds\int_a^b dm} = \frac{\ds\int_a^b z \delta dz}{\ds\int_a^b \delta dz}.$$ Feel free to use software. Verify that $\bar z = \frac{2a+b}{3}$.
Above we performed computations for a rod that lies on an axis. This works great for a drive shaft, or antenna, or any part of the rover that consists of a straight thin rod. But we can repeate these computations for a portion of the rover that is a thin flat plate, such as a solar panel, an armored plate, or any object which is best described by thinking of the area.
- Consider the triangular region $R$ in the first quadrant that lies under the line $\ds\frac{x}{a}+\frac{y}{b}=1$. If you would rather work with numbers instead of variables, feel free to let $a=5$ and $b=7$ in this problem.
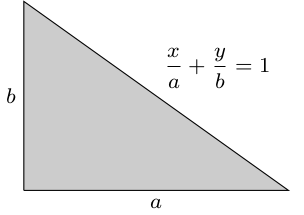
- Compute the double integral $\ds\int_0^a\int_0^{b(1-\frac{x}{a})} dy dx$. What physical quantity of the region $R$ does this integral give?
- The density of the metal plate is $\delta$ g/m$^2$. Set up a double integral formula to compute the mass of the region using this density.
- The center-of-mass in the $x$-direction is given by the formula $$\bar x = \frac{\ds\iint_R xdm}{\ds\iint_R dm}= \frac{\ds\int_0^a\int_0^{b(1-\frac{x}{a})} x \delta dy dx}{\ds\int_0^a\int_0^{b(1-\frac{x}{a})} \delta dy dx}.$$ Assuming $\delta$ is constant, compute this integral and show that $\bar x = \frac{a}{3}$. Feel free to use software.
- Set up an integral formula, like the one above, to compute $\bar y$. Show the integral formula you used, and then state the value $\bar y$ obtained.
Task 27.2
- Consider the region $R$ in the $xy$-plane that is below the line $y=x+2$, above the line $y=2$, and left of the line $x=5$. We can describe this region by saying for each $x$ with $0\leq x\leq 5$, we want $y$ to satisfy $2\leq y\leq x+2$. In set builder notation, we write $$R=\{(x,y)\in \mathbb{R}^2\mid 0\leq x\leq 5, 2\leq y\leq x+2\}.$$ We use the symbols $\{$ and $\}$ to enclose sets and the symbol $\mid$ for "such that". We read the above line as "$R$ equals the set of $(x,y)$ in the plane such that zero is less than $x$ which is less than 5, and 2 is less than $y$ which is less than $x+2$." The iterated double integral $\int_0^5\int_2^{x+2} dy dx$ gives the area of this region.
- Draw this region.
- Describe the region $R$ by saying for each $y$ with $c\leq y\leq d$, we want $x$ to satisfy $a(y)\leq x\leq b(y)$. In other words, find constants $c$ and $d$, and functions $a(y)$ and $b(y)$, so that for each $y$ between $c$ and $d$, the $x$ values must be between the functions $a(y)$ and $b(y)$. Write your answer using the set builder notation $$R=\{(x,y)\ | \ c\leq y\leq d, a(y)\leq x\leq b(y)\}.$$
- Finish setting up the iterated double integral $\int_?^?\int_?^? dx dy$.
- Compute both $\int_0^5\int_2^{x+2} dy dx$ and $\int_?^?\int_?^? dx dy$ (the integral you just set up), and verify that they give the same value.
- Consider the iterated integral $\ds \int_0^3\int_x^3 e^{y^2}dydx$. We could think of the function $e^{y^2}$ as a density, but notice that this function is independent of the region described by the bounds of the integral.
- Write the bounds as two inequalities ($0\leq x\leq 3$ and $?\leq y\leq ?$). Then draw and shade the region $R$ described by these two inequalities.
- Swap the order of integration from $dydx$ to $dxdy$. This forces you to describe the region using two inequalities of the form $c\leq y\leq d$ and $a(y)\leq x\leq b(y)$, obtaining the iterated double integral $\ds \int_?^?\int_?^? e^{y^2}dxdy$.
- Use your new bounds to compute the integral by hand.
- Why is the original integral $\ds \int_0^3\int_x^3 e^{y^2}dydx$ impossible to compute without first swapping the order of integration [Hint: Try computing the inner integral $\int_x^3 e^{y^2}dy$ -- why can't you? What does Mathematica give if you try to compute this inner integral?]
Task 27.3
I won't add another task. Work on the previous tasks, and come ready to discuss them.
Task 27.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
