Task 19.1
In the first calculus books, there was no mention of the chain rule. This is because differentials were extremely common notation, and the chain rule, when working with differentials, is simply substitution. In this task, we'll develop some rules for how to compute derivatives when functions depend on other functions (so composite functions).
- Suppose that $f(x,y,z) = ax+by+cz$, and $x=mt$, $y=nt$, and $z = pt$, for some constants $a,b,c,m,n,p$. Compute the differentials $df$, $dx$, $dy$, and $dz$. Then use substitution to obtain the differential of $f$ in terms of $t$ and $dt$. Finish by stating $\frac{df}{dt}$.
- Suppose now that $g$ is a function of $x$ and $y$, but $x$ and $y$ are functions of $u$, $v$, and $w$. This means, by definition of the differential and partial derivatives, that $dg = g_xdx+g_ydy$, along with $dx = x_udu+x_vdv+x_wdw$ and $dy = y_udu+y_vdv+y_wdw$. Substitution gives $$\begin{align*} dg &= g_xdx+g_ydy\\ &= g_x(x_udu+x_vdv+x_wdw)+g_y(y_udu+y_vdv+y_wdw)\\ &= (?)du+(?)dv+ (?)dw. \end{align*}$$ Fill in the question marks above, and then use your answer to state the three partials $\dfrac{\partial g}{\partial u}$, $g_v$, and $D_w g$.
- Consider the function $h(x,y,z)$, where $x$, $y$, and $z$ are functions of $r$ and $\theta$. State the differentials of $h$, $x$, $y$, and $z$, and then use substitution to prove that $$\dfrac{\partial h}{\partial r} = \dfrac{\partial h}{\partial x}\dfrac{\partial x}{\partial r} +\dfrac{\partial h}{\partial y}\dfrac{\partial y}{\partial r} +\dfrac{\partial h}{\partial z}\dfrac{\partial z}{\partial r}.$$ Obtain a similar formula for $\dfrac{\partial h}{\partial \theta}$.
Feel free to ask me in class how this relates to matrix multiplication.
Task 19.2
Suppose a rover travels around the circle $g(x,y)=x^2+y^2=1$. The elevation of the surrounding terrain is $f(x,y) = x^2+y+4$. The plot below shows the rover's path (the constraint $g(x,y)=1$), placed on the same grid as a contour plot of the elevation (the function $f(x,y)$ we wish to optimize).
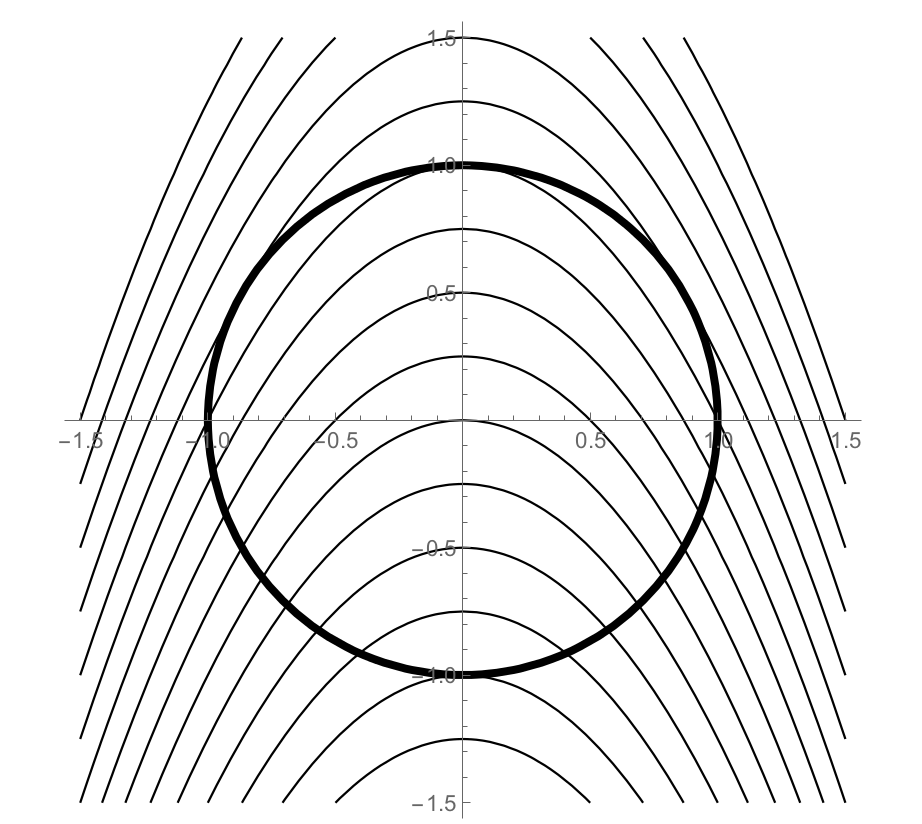
Each level curve above represents a difference in elevation of 0.25 m. Our goal is to find the maximum and minimum elevation reached by the rover as it travels around the circle. We will optimize $f(x,y)$ subject to the constraint $g(x,y)=1$.
- Label each level curve with its elevation. Print this page, or copy the curves down on your paper.
- At which $(x,y)$ point does the rover encounter the minimum elevation? What is the minimum elevation? Explain, using the plot.
- Suppose the rover is currently at the point $(0,1)$ on its circular path. As the rover moves left, will the elevation rise or fall? What if the rover moves right? Is $(0,1)$ the location of a local maximum or local minimum?
- On your graph, place a dot(s) where the rover reaches a maximum elevation. What is the maximum elevation? Explain.
- Rather than visually inspecting level curves, let's examine the gradients $\vec \nabla f$ and $\vec \nabla g$ to see how these gradients compare at maximums and minimums.
- On the graph above, draw $\vec \nabla f$ at lots of places on your contour plot.
- At lots of points on the circle, with a different color, draw $\vec \nabla g$.
- Make sure you draw both gradients at all the points corresponding to local maxes and mins.
- At the local maximums and minimums, Lagrange noticed that $\vec \nabla f = \lambda \vec \nabla g$.
- How would you interpret the equation $\vec \nabla f = \lambda \vec \nabla g$?
- Compute $\vec \nabla f$ and $\vec \nabla g$.
- Explain why the system of equations $\vec \nabla f = \lambda \vec \nabla g$ and $g(x,y)=c$ is equivalent to the system of equations $$2x = \lambda 2x,\quad 1=\lambda 2y,\quad x^2+y^2=1.$$
- Solve the system of equations above to obtain 4 ordered pairs $(x,y)$. You can use the Mathematica notebook LagrangeMultipliers.nb to check your work.
- At each ordered pair, find the elevation. What is the maximum elevation obtained, and where does it occur? What is the minimum elevation obtained, and where does it occur?
Suppose $f$ and $g$ are continuously differentiable functions. Suppose that we want to find the maximum and minimum values of $f(x,y)$ subject to the constraint $g(x,y)=c$ (where $c$ is some constant). If a local maximum or minimum occurs, it must occur at a spot where the gradient of $f$ and the gradient of $g$ point in the same, or opposite, directions. This means the gradient of $g$ must be a multiple of the gradient of $f$. To find the $(x,y)$ locations of the maximum and minimum values (if they exist), we solve the system of equations that result from $$\vec \nabla f = \lambda \vec \nabla g,\quad \text{and}\quad g(x,y)=c$$ where $\lambda$ is the proportionality constant. The locations of maximum and minimum values of $f$ will be among the solutions of this system of equations.
Task 19.3
This task will mostly involve reading through some definitions and an example, with a short example at the end.
Let $A$ be a square matrix, as $A=\begin{bmatrix} \begin{pmatrix}a\\b\end{pmatrix}& \begin{pmatrix}c\\d\end{pmatrix}\end{bmatrix} = \begin{bmatrix}a&c\\b&d\end{bmatrix}$. The eigenvalues $\lambda$ and eigenvectors $\vec x$ of $A$ are solutions $\lambda$ and $\vec x\neq \vec 0$ to the equation $A\vec x=\lambda \vec x$, effectively replacing the matrix product (linear combination) with scalar multiplication.
The identity matrix $I$ is a square matrix with 1's on the diagonal and zeros everywhere else, so in 2D we have $I = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}$. To find the eigenvalues, we rewrite $A\vec x = \lambda\vec x$ in the form $A\vec x -\lambda\vec x=\vec 0$ or $A\vec x -\lambda I \vec x=\vec 0$, which becomes $(A-\lambda I) =\vec 0.$ We need to find the values $\lambda$ so that $\left(\begin{bmatrix} a&c\\b&d\end{bmatrix}-\lambda \begin{bmatrix} 1&0\\0&1 \end{bmatrix} \right)\begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}0\\0\end{pmatrix} \quad\text{or}\quad \begin{bmatrix} a-\lambda &c\\b&d-\lambda \end{bmatrix}\begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}0\\0\end{pmatrix}.$ A linear algebra course will show that $\lambda$ satisfies $$(a-\lambda)(d-\lambda)-bc=0.$$
Let $f(x,y)$ be a function so that all the second partial derivatives exist and are continuous. The second derivative of $f$, written $D^2f$ and sometimes called the Hessian of $f$, is a square matrix. Suppose $P=(a,b)$ is a critical point of $f$, meaning $\vec\nabla f(a,b) = (0,0)$.
- Suppose all the eigenvalues of $D^2f(a,b)$ are positive. Then at all points $(x,y)$ sufficiently near $P$, the gradient $\vec \nabla f(x,y)$ points away from $P$. The function has a local minimum at $P$.
- Suppose all the eigenvalues of $D^2f(a,b)$ are negative. Then at all points $(x,y)$ sufficiently near $P$, the gradient $\vec \nabla f(x,y)$ points inwards towards $P$. The function has a local maximum at $P$.
- Suppose the eigenvalues of $D^2f(a,b)$ differ in sign. Then at some points $(x,y)$ near $P$, the gradient $\vec \nabla f(x,y)$ points inwards towards $P$. However, at other points $(x,y)$ near $P$, the gradient $\vec \nabla f(x,y)$ points away from $P$. The function has a saddle point at $P$.
- If the largest or smallest eigenvalue of $f$ equals 0, then the second derivative tests yields no information.
Let's look at an example. Consider $f(x,y)=x^2-2x+xy+y^2$. The gradient is $\vec \nabla f(x,y)=(2x-2+y,x+2y)$. The critical points of $f$ occur where the gradient is zero. We need to solve the system $2x-2+y=0$ and $x+2y=0$, which is equivalent to solving $2x+y=2$ and $x+2y=0$. Double the second equation, and then subtract it from the first to obtain $0x-3y=2$, or $y=-2/3$. The second equation says that $x=-2y$, or that $x=4/3$. So the only critical point is $(4/3,-2/3)$.
The second derivatives is $ D^2f = \begin{bmatrix}2&1 \\1&2\end{bmatrix}.$ The second derivative is constant, so $D^2 f(4/3,-2/3)$ is the same as $D^2f(x,y)$. (In general, the critical point may affect your matrix.) To find the eigenvalues we solve $$(2-\lambda)(2-\lambda)-(1)(1)=0.$$ Expanding the left hand side gives $4-4\lambda + \lambda^2 -1 = 0$. Simplifying and factoring gives us $\lambda^2-4\lambda +3 = (\lambda-3)(\lambda -1) = 0$. The eigenvalues are $\lambda = 1$ and $\lambda=3$. Since both numbers are positive, we know the gradient points outwards away from the critical point. The critical point $(4/3,-2/3)$ corresponds to a local minimum of the function. The local minimum is the output $f(4/3,-2/3) = (4/3)^2-2(4/3)+(4/3)(-2/3)+(-2/3)^2$.
Let's try this process on our own. Consider the function $f(x,y)=x^2+4xy+y^2$.
- Find the critical points of $f$ by finding when $Df(x,y)$ is the zero matrix.
- Find the eigenvalues of $D^2f$ at any critical points.
- Label each critical point as a local maximum, local minimum, or saddle point, and state the value of $f$ at the critical point.
Task 19.4
Pick some problems related to the topics we are discussing from the Text Book Practice page.
